Skip to main content
SpringerLink
Log in

Analysis of the Problem of Harmonic Waves in Elastic Bodies and its h-Adaptive Finite-Element Approximation

  • Published:
Journal of Mathematical Sciences Aims and scope Submit manuscript

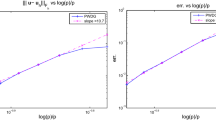
We formulate a variational problem for harmonic waves in a viscoelastic body with short-term memory generated by distributed loads of a given frequency. The conditions of its well-posedness and equivalence to the saddle-point problem for the corresponding Lagrangian are established. We construct an h -adaptive scheme of the finite-element method for the solution of the formulated problem with an a posteriori error estimator determined element by element and a criterion for the local improvement of Delaunay triangulations used for the evaluation of approximations with prescribed accuracy. The efficiency of the proposed methods is illustrated by an example of numerical investigation of the resonance frequencies of a square plate containing a square hole.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. H. Kvasnytsia, F. Chaban, and H. Shynkarenko, “Analysis of the problems of forced harmonic vibration of elastic bodies and the construction of reliable FEM approximations of their solutions,” Visn. Lviv. Univ., Ser. Prykl. Mat. Inform., Issue 20, 19–33 (2013).

  2. H. Kvasnytsia and H. Shynkarenko, “Adaptive approximations of the finite-element method for the problems of elastostatics,” Visn. Lviv. Univ., Ser. Prykl. Mat. Inform., Issue 5, 95–106 (2002).

  3. H. Kvasnytsia and H. Shynkarenko, “Comparison of simple a posteriori error estimators of the finite-element method for the problems of elastostatics,” Visn. Lviv. Univ., Ser. Prykl. Mat. Inform., Issue 7, 162–174 (2003).

  4. V. M. Trushevs’kyi, H. A. Shynkarenko, and N. M. Shcherbyna, Finite-Element Method and Artificial Neural Networks: Theoretical Aspects and Applications [in Ukrainian], Izd. I. Franko National University of Lviv, Lviv (2014).

  5. F. V. Chaban and H. A. Shynkarenko, “A posteriori error estimators of finite-element approximations for problems of forced harmonic vibrations of piezoelectrics,” Mat. Met. Fiz.-Mekh. Polya, 52, No. 4, 88–98 (2009); English translation: J. Math. Sci., 174, No. 2, 229–242 (2011); DOI: https://doi.org/10.1007/s10958-011-0293-y.

  6. M. Ainsworth and J. T. Oden, A Posteriori Error Estimation in Finite Element Analysis, Wiley, New York (2000).

    Book  MATH  Google Scholar 

  7. I. Babuška, J. R. Whiteman, and T. Strouboulis, Finite Elements: an Introduction to the Method and Error Estimation, Oxford Univ. Press, Oxford (2011).

    MATH  Google Scholar 

  8. R. Dautray and J.-L. Lions, Mathematical Analysis and Numerical Methods for Science and Technology, Vol. 2: Functional and Variational Methods, Springer, Berlin (2000).

  9. C. W. de Silva, Vibration Damping, Control, and Design, CRC Press, Boca Raton (2007).

    Book  MATH  Google Scholar 

  10. G. Duvaut and J.-L. Lions, Inequalities in Mechanics and Physics, Springer, Berlin (1976).

    Book  MATH  Google Scholar 

  11. F. Ebrahimi (editor), Advances in Vibration Analysis Research, InTech, Rijeka (2011).

  12. J. Nečas, Direct Methods in the Theory of Elliptic Equations, Springer, Berlin (2012).

    Book  MATH  Google Scholar 

  13. J. Nečas and I. Hlaváček, Mathematical Theory of Elastic and Elasto-Plastic Bodies: An Introduction, Elsevier, Amsterdam (1981).

    MATH  Google Scholar 

  14. R. Ohayon and C. Soize, Structural Acoustic and Vibration, Academic Press, London (1998).

    MATH  Google Scholar 

  15. M. Petyt, Introduction to Finite Element Vibration Analysis, Cambridge Univ. Press, Cambridge (1990); https://doi.org/10.1002/zamm.19920720323.

    Book  MATH  Google Scholar 

  16. R. Verfürth, A Posteriori Error Estimation Techniques for Finite Element Methods, Oxford Univ. Press, Oxford (2013); DOI: https://doi.org/10.1093/acprof:oso/9780199679423.001.0001.

    Book  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. I. Franko National University of Lviv, Lviv, Ukraine

    H. А. Kvasnytsia & H. А. Shynkarenko

  2. Opole University of Technology, Opole, Poland

    H. А. Shynkarenko

Authors
  1. H. А. Kvasnytsia
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. H. А. Shynkarenko
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to H. А. Kvasnytsia.

Additional information

Translated from Matematychni Metody ta Fizyko-Mekhanichni Polya, Vol. 63, No. 1, pp. 52–64, January–March, 2020.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kvasnytsia, H.А., Shynkarenko, H.А. Analysis of the Problem of Harmonic Waves in Elastic Bodies and its h-Adaptive Finite-Element Approximation. J Math Sci 270, 59–75 (2023). https://doi.org/10.1007/s10958-023-06332-1

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10958-023-06332-1

Keywords

Search

Navigation