Klein Sail and Diophantine Approximation of a Vector

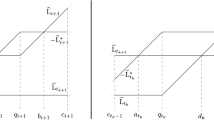
In the papers by V. I. Arnold and his successors based upon the ideas of H. Poincaré and F. Klein, it was the Klein sail associated with an operator in ℝⁿ that they considered to play the role of a multidimensional continued fraction, and in these terms generalizations of Lagrange’s theorem on continued fractions were formulated. A different approach to generalization of the notion of continued fraction was based upon modifications of Euclid’s algorithm for constructing, given an irrational vector, an approximating sequence of rational vectors.

We suggest a modification of the Klein sail that is constructed directly from a vector, without any operator. We introduce a numeric characteristic of a Klein sail, its asymptotic anisotropy associated with a one-parameter transformation semigroup of the lattice generating the sail and of its Voronoi cell. In terms of this anisotropy, we hope to give a geometric characterization of irrational vectors worst approximated by rational ones. In the three-dimensional space, we suggest a vector (related to the smallest Pisot–Vijayaraghavan number) that is a candidate for this role. This vector may be called an analog of the golden number, which is the real number worst approximated by rationals in the classical theory of Diophantine approximations.