Analytical and Numerical Solution of the Problem on Brachistochrones in some General Cases

Abstract

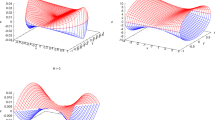
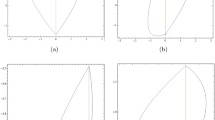
In this paper, we discuss J. Bernoulli’s brachistochrone problem and find its analytical and numerical solutions in the cases where viscous or dry friction are taken into account. We predict the existence of a point of “geometrical phase transition” u₀ = ln(1/2k₂b); it corresponds to the transition from one class of trajectories to another that qualitatively differs from the initial class. Numerical simulation of the motion in a neighborhood of points of geometric phase transitions is performed. We prove that in the absence of friction forces, the minimization problem for the motion time for any motion along a curvilinear trough under the action of the gravity force can always be reduced to the brachistochrone problem and can be solved without involving methods of calculus of variation, only by general dynamical laws. We find a solution to the classical Bernoulli problem under the condition that the length of the trajectory is fixed. We show that under this isoperimetric condition, the class of trajectories differs from the classical brachistochrone. We also observe the transformation of these trajectories to the cycloid by numerical and analytical analysis.