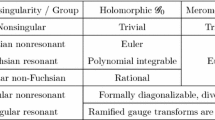
Each component of any solution of a Fuchsian differential system satisfies a Fuchsian differential equation. The set of Fuchsian systems is fibered into equivalence classes. Each class consists of systems with similar sets of matrix residues, the conjugation matrix being the same for all elements of the set. We investigate the corresponding classes of scalar equations.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
R. Fuchs, “Über lineare homogene Differentialgleitungen zweiter Ordnung mit drei im Endlichen gelegenen wesentlich Singularitaeten,” Math. Ann., 163, 301–321 (1907).
S. Slavyanov, “Painlevé equations as classical analogues of Heun equations,” J. Phys. A, 29, 7329–7335 (1996).
S. Slavyanov, “Antiquantization and the corresponding symmetries,” Theoret. Math. Phys., 185, 1522–1526 (2015).
D. V. Anosov and A. A. Bolibruch, The Riemann–Hilbert Problem, Vieweg, Braunschweig (1994).
A. Bolibruch, Monodromy Inverse Problems of the Analytic Theory of Differential Equations [in Russian], MCCME, Moscow (2009).
A. Its and V. Novokshenov, The Isomonodromic Deformation Method in the Theory of Painlevé Equations, Lect. Notes Math., 1191, Springer, Berlin–New York (1986).
A. Kapaev, “Lax pairs for Painlevé equations,” in: Isomonodromic Deformations and Applications in Physics, CRM Proc. Lect. Notes, 31, Amer. Math. Soc., Providence, Rhode Island (2002), pp. 37–48.
V. Gromak, I. Laine, and S. Shimomura, Painlevé Differential Equations in the Complex Domain, De Gruyter, Berlin (2002).
A. Bruno and A. Bathin (eds.), Painleve Equations and Related Topics, De Gruyter, Berlin–Boston (2012).
S. Slavyanov and W. Lay, Special Functions: A Unified Theory Based on Singularities, Oxford Univ. Press, Oxford–New York (2002).
A. Ronveau (ed.), Heun’s Differential Equation, Oxford Univ. Press, Oxford–New York–Tokyo (1995).
A. Kazakov and S. Slavyanov, “Symmetries of Heun equations and Okamoto transformations for Kovalevskaya–Painlevé equations,” Theoret. Math. Phys., 155, 721–732 (2008).
S. Slavyanov et al., “Generation and removal of apparent singularities in linear ordinary differential equations with polynomial coefficients,” Theoret. Math. Phys., 189, 1726–1733 (2016).
S. Slavyanov, “Symmetries and apparent singularities for simplest Fuchsian equations,” Theoret. Math. Phys., 193, 1754–1760 (2017).
K. Iwasaki, H. Kimura, S. Shimomura, and M. Iosida, From Gauss to Painlevé. A Modern Theory of Special Functions, Vieweg, Braunschweig (1991).
Author information
Authors and Affiliations
Corresponding author
Additional information
Translated from Zapiski Nauchnykh Seminarov POMI, Vol. 468, 2018, pp. 221–227.
Rights and permissions
About this article
Cite this article
Babich, M.V., Slavyanov, S.Y. Relations Between Second-Order Fuchsian Equations and First-Order Fuchsian Systems. J Math Sci 240, 646–650 (2019). https://doi.org/10.1007/s10958-019-04381-z
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10958-019-04381-z