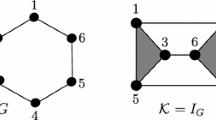
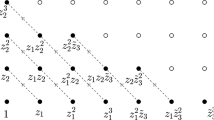
A principal circle bundle over a PL polyhedron can be triangulated and thus obtains combinatorics. The triangulation is assembled from triangulated circle bundles over simplices. To every triangulated circle bundle over a simplex we associate a necklace (in the combinatorial sense). We express rational local formulas for all powers of the first Chern class in terms of expectations of the parities of the associated necklaces. This rational parity is a combinatorial isomorphism invariant of a triangulated circle bundle over a simplex, measuring the mixing by the triangulation of the circular graphs over vertices of the simplex. The goal of this note is to sketch the logic of deducing these formulas from Kontsevitch’s cyclic invariant connection form on metric polygons.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
J.-L. Brylinski, Loop Spaces, Characteristic Classes and Geometric Quantization, reprint of the 1993 edition, Birkhäuser Basel (2008).
S. Chern, “Circle bundles,” in: J. Palis and M. do Carmo (eds.), Geometry and Topology, Lecture Notes Math., Vol. 597, Springer, Berlin–Heidelberg (1977), pp. 114–131.
M. M. Cohen, “Simplicial structures and transverse cellularity,” Ann. Math. (2), 85, 218–245 (1967).
S. Duzhin and D. Pasechnik, “Automorphisms of necklaces and sandpile groups,” arXiv:1304.2563 (2013).
J. L. Dupont, “Simplicial De Rham cohomology and characteristic classes of flat bundles,” Topology, 15, 233–245 (1976).
A. A. Gaĭfullin, “Computation of characteristic classes of a manifold from its triangulation,” Uspekhi Mat. Nauk, 60, No. 4(364), 37–66 (2005).
A. M. Gabrielov, I. M. Gelfand, and M. V. Losik, “Combinatorial calculus of characteristic classes,” Funct. Anal. Appl., 9, 186–202 (1976).
I. M. Gelfand and R. D. MacPherson, “A combinatorial formula for the Pontrjagin classes,” Bull. Amer. Math. Soc. New Ser., 26, No. 2, 304–309 (1992).
R. M. Goresky, “Triangulation of stratified objects,” Proc. Amer. Math. Soc., 72, 193–200 (1978).
A. Hatcher, Algebraic Topology, Cambridge Univ. Press (2001).
S. Halperin and D. Toledo, “Stiefel–Whitney homology classes,” Ann. Math. (2), 96, 511–525 (1972).
K. Igusa, Higher Franz–Reidemeister Torsion, Amer. Math. Soc., Providence, Rhode Island; International Press, Somerville, Massachusetts (2002).
K. Igusa, “Combinatorial Miller–Morita–Mumford classes and Witten cycles,” Algebr. Geom. Topol., 4, 473–520 (2004).
K. Igusa and J. Klein, “The Borel regulator map on pictures. II: An example from Morse theory,” K-Theory, 7, No. 3, 225–267 (1993).
M. Ishikawa and M. Wakayama, “Minor summation formula of Pfaffians,” Linear Multilinear Algebra, 39, No. 3, 285–305 (1995).
M. Jungerman and G. Ringel, “Minimal triangulations on orientable surfaces,” Acta Math., 145, 121–154 (1980).
M. É. Kazarian, “Relative Morse theory of one-dimensional bundles and cyclic homology,” Funct. Anal. Appl., 31, No. 1, 16–24 (1997).
M. É. Kazarian, “The Chern–Euler number of circle bundle via singularity theory,” Math. Scand., 82, No. 2, 207–236 (1998).
M. Kontsevich, “Intersection theory on the moduli space of curves and the matrix Airy function,” Comm. Math. Phys., 147, No. 1, 1–23 (1992).
D. Kozlov, Combinatorial Algebraic Topology, Springer, Berlin (2008).
J.-L. Loday, Cyclic Homology, Springer-Verlag, Berlin (1998).
J. Lurie, “Algebraic K-Theory and Manifold Topology,” lecture course, 2014; http://www.math.harvard.edu/~lurie/281.html.
C. Manolescu, “Pin(2)-equivariant Seiberg–Witten Floer homology and the triangulation conjecture,” arXiv:1303.2354 (2014).
K. V. Madahar and K. S. Sarkaria, “A minimal triangulation of the Hopf map and its application,” Geom. Dedicata, 82, Nos. 1–3, 105–114 (2000).
Author information
Authors and Affiliations
Corresponding author
Additional information
Published in Zapiski Nauchnykh Seminarov POMI, Vol. 448, 2016, pp. 201–235.
Rights and permissions
About this article
Cite this article
Mnev, N., Sharygin, G. On Local Combinatorial Formulas for Chern Classes of a Triangulated Circle Bundle. J Math Sci 224, 304–327 (2017). https://doi.org/10.1007/s10958-017-3416-2
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10958-017-3416-2