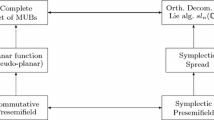
The goal of our article is a study of related mathematical and physical objects: orthogonal pairs in sl(n) and mutually unbiased bases in ℂn . An orthogonal pair in a simple Lie algebra is a pair of Cartan subalgebras that are orthogonal with respect to the Killing form. The description of orthogonal pairs in a given Lie algebra is an important step in the classification of orthogonal decompositions, i.e., decompositions of the Lie algebra into a direct sum of Cartan subalgebras pairwise orthogonal with respect to the Killing form. One of the important notions of quantum mechanics, quantum information theory, and quantum teleportation is the notion of mutually unbiased bases in the Hilbert space ℂn . Two orthonormal bases {e i } n i = 1 , {f j } n j = 1 are mutually unbiased if and only if \( {\left|\left\langle {e}_i\left|{f}_j\right.\right\rangle \right|}^2=\frac{1}{n} \) for any i, j = 1,…, n. The notions of mutually unbiased bases in ℂn and orthogonal pairs in sl(n) are closely related. The problem of classification of orthogonal pairs in sl(n) and the closely related problem of classification of mutually unbiased bases in ℂn are still open even for the case n = 6. In this article, we give a sketch of our proof that there is a complex four-dimensional family of orthogonal pairs in sl(6). This proof requires a lot of algebraic geometry and representation theory. Further, we give an application of the result on the algebraic geometric family to the study of mutually unbiased bases. We show the existence of a real four-dimensional family of mutually unbiased bases in ℂ6 , thus solving a long-standing problem. Bibliography: 24 titles.
Similar content being viewed by others
References
A. Bondal and I. Zhdanovskiy, “Representation theory for system of projectors and discrete Laplace operator,” Preprint of IPMU, IPMU13-0001 (2013).
A. Bondal and I. Zhdanovskiy, “Simplectic geometry of unbiasedness and critical points of a potential,” arxiv:1507.00081.
A. Bondal and I. Zhdanovskiy, “Orthogonal pairs for Lie algebra sl(6),” Preprint of IPMU, IPMU14-0296 (2014).
P. O. Boykin, M. Sitharam, P. H. Tiep, and P. Wocjan, “Mutually unbiased bases and orthogonal decompositions of Lie algebras,” Quantum Inf. Comput., 7, 371–382 (2007).
M. D. de Burgh, N. K. Landford, A. C. Doherty, and A. Gilchrist, “Choice of measurement sets in qubit tomography,” Phys. Rev. A, 78, 052122 (2008).
W. Crawley-Boevey, “Noncommutative deformations of Kleinian singularities,” Duke Math. J., 92, No. 3, 605–635 (1998).
W. Crawley-Boevey, “Geometry of the moment map for representations of quivers,” Compos. Math., 126, 257–293 (2001).
T. Durt, B.-G. Englert, I. Bengtsson, and K. Zyczkowski, “On mutually unbiased bases,” Int. J. Quantum Inform., 8, 535–640 (2010).
S. N. Filippov and V. I. Man’ko, “Mutually unbiased bases: tomography of spin states and the star-product scheme,” Phys. Scripta, 2011, T143.
W. L. Gan and V. Ginzburg, “Deformed preprojective algebras and symplectic reflection for wreath products,” J. Algebra, 283, 350–363 (2005).
U. Haagerup, “Orthogonal maximal abelian *-subalgebras of the n×n matrices and cyclic n-roots,” in: Operator Algebras and Quantum Field Theory, International Press, Cambridge, Massachusetts (1996), pp. 296–322.
C. D. Hacon, J. McKernan, and C. Xu, “On the birational automorphisms of varieties of general type,” Ann. Math., 177, 1077–1111 (2013).
D. N. Ivanov, “An analogue of Wagner’s theorem for orthogonal decompositions of the algebra of matrices M n (C),” Uspekhi Mat. Nauk, 49, No. 1(225), 215–216 (1994).
A. I. Kostrikin, T. A. Kostrikin, and V. A. Ufnarovskii, “Orthogonal decompositions of simple Lie algebras (type A n ),” Trudy Mat. Inst. Steklov., 158, 105–120 (1981).
A. I. Kostrikin, I. A. Kostrikin, and V. A. Ufnarovskii, “On the uniqueness of orthogonal decompositions of Lie algebras of type A n and C n ,” Mat. Issled., 74, 80–105 (1983).
A. I. Kostrikin and P. H. Tiep, Orthogonal Decompositions and Integral Lattices, Walter de Gruyter (1994).
G. Lima, L. Neves, R. Guzman, E. S. Gomez, W. A. T. Nogueira, A. Delgado, A. Vargas, and C. Saavedra, “Experimental quantum tomography of photonic qudits via mutually unbiased basis,” Optics Express, 19, No. 4, 3542–3552 (2011).
M. Matolcsi and F. Szöllȍsi, “Towards a classification of 6×6 complex Hadamard matrices,” Open. Syst. Inf. Dyn., 15, 93–108 (2008).
K. Nomura, “Type II matrices of size five,” Graphs Combin., 15, No. 1, 79–92 (1999).
qig.itp.uni-hannover.de/qiproblems/Main Page.
M. B. Ruskai, “Some connections between frames, mutually unbiased bases, and POVM’s in quantum information theory,” Acta Appl. Math., 108, No. 3, 709–719 (2009).
F. Szöllȍsi, “Complex Hadamard matrices of order 6: a four-parameter family,” J. London Math. Soc., 85, No. 3, 616–632 (2012).
J. Thompson, “A conjugacy theorem for E 8,” J. Algebra, 38, No. 2, 525–530 (1976).
W. Tadej and K. Zyczkowski, “Defect of a unitary matrix,” Linear Algebra Appl., 429, 447–481 (2008).
Author information
Authors and Affiliations
Corresponding author
Additional information
Published in Zapiski Nauchnykh Seminarov POMI, Vol. 437, 2015, pp. 35–61.
Rights and permissions
About this article
Cite this article
Bondal, A., Zhdanovskiy, I. Orthogonal Pairs and Mutually Unbiased Bases. J Math Sci 216, 23–40 (2016). https://doi.org/10.1007/s10958-016-2885-z
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10958-016-2885-z