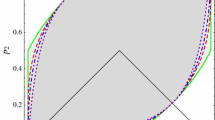
A bound for the remainder in the Esseen expansion is obtained in the case of Bernoulli random variables. The bound consists of two parts, uniform and non-uniform. The uniform part depends only on n and p, and the non-uniform part depends also on x. This bound is compared with other known bounds. It is shown how this result can be applied to the problem of the absolute constant in the Berry–Esseen inequality.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
S. V. Nagaev and V. I. Chebotarev, “On the bound of proximity of the binomial distribution to the normal one,” Theory Probab. Appl., 56, No. 2, 213–239 (2012).
C.-G. Esseen, “A moment inequality with an application to the central limit theorem,” Scand. Actuar. J., 3–4, 160–170 (1956).
V. M. Zolotarev, “An absolute estimate of the remainder in the central limit theorem,” Teor. Veroyatn. Primen., 11, No. 1, 108–119 (1966).
V. M. Zolotarev, “A sharpening of the inequality of Berry–Esseen,” Z. Wahrscheinlichkeitstheor. verw. Geb., 8, 332–342 (1967).
I.G. Shevtsova, “On the smoothing inequality,” Dokl. Akad. Nauk, 430, No. 5, 600–602 (2010).
H. Prawitz, “Limits for a Distributions, if the Characteristic Function is given in a Finite Domain,” Skand. Aktuar. J., 55, 138–154 (1972).
C.-G. Esseen, “Fourier analysis of distribution function. A muthematical study of the Laplace–Gaussian law,” Acta Math., 77, 1–125 (1945).
B. V. Gnedenko and A.N. Kolmogorov, Limit Distributions for Sums of Independent Random Variables, Gos. Izd. Tekhn.-Teor. Lit., Moscow, Leningrad (1949).
H. Bergstr¨om, “On asymptotic expansions of probability functions,” Skand. Aktuar. J., 1–2, 1–34 (1951).
A.M. Zubkov and A.A. Serov, “A complete proof of universal inequalities for distribution function of binomial law,” Theory Probab. Appl., 57, No. 3, 539–544 (2013).
D. Alfers and H. Dinges, “A normal approximation for Beta and Gamma tail probabilities,” Z. Wahrscheinlichkeitstheor. Verw. Geb., 65, 399–420 (1984).
J. V. Uspensky, Introduction to Mathematical Probability, McGraw Hill, New York (1937).
I. G. Shevtsova, Optimization of the structure of the moment bounds for accuracy of normal approximation for the distributions of sums of independent random variables, Dissertation for the degree of Doctor of Physico–Mathematical Sciences, Moscow State University, Moscow (2013).
W. Feller. “Generalization of a probability limit theorem of Cram´er,” Trans. Am. Math. Soc., 54, No. 3, 361–372 (1943).
C. L´enart, “On certain theorems of Berry and a limit theorem of Feller,” Mat. ˇ Casopis, 18, No. 1, 59–75 (1968).
V.V. Senatov, “About non-uniform bounds of approximation accuracy,” Theory Probab. Appl., 59, No. 2, 276–312 (2013).
A.C. Berry, “The accuracy of the Gaussian approximation to the sum of independent variates”, Trans. Am. Math. Soc., 49, 122–136 (1941).
Author information
Authors and Affiliations
Corresponding author
Additional information
Proceedings of the XXXII International Seminar on Stability Problems for Stochastic Models, Trondheim, Norway, June 16–21, 2014.
Rights and permissions
About this article
Cite this article
Nagaev, S.V., Chebotarev, V.I. & Zolotukhin, A.Y. A Non-Uniform Bound of the Remainder Term in the Central Limit Theorem for Bernoulli Random Variables. J Math Sci 214, 83–100 (2016). https://doi.org/10.1007/s10958-016-2759-4
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10958-016-2759-4