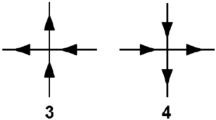
We consider the five-vertex model on an M ×2N lattice with fixed boundary conditions of special type. We discuss a determinantal formula for the partition function in application to description of various enumerations of N × N × (M − N) boxed plane partitions. It is shown that at the free-fermion point of the model, this formula reproduces the MacMahon formula for the number of boxed plane partitions, while for generic weights (outside the free-fermion point), it describes enumerations with the weight depending on the cumulative number of jumps along vertical (or horizontal) rows. Various representations for the partition function which describes such enumerations are obtained.
Similar content being viewed by others
References
L. A. Takhtajan and L. D. Faddeev, “Quantum inverse scattering method and the Heisenberg XYZ model,” Usp. Mat. Nauk, 34, 13–63 (1979).
V. E. Korepin, N. M. Bogoliubov, and A. G. Izergin, Quantum Inverse Scattering Method and Correlation Functions, Cambridge Univ. Press, Cambridge (1993).
P. P. Kulish, “Quantum difference nonlinear Schrödinger equation,” Lett. Math. Phys., 5, 191–197 (1981).
V. S. Gerdjikov, M. I. Ivanov, and P. P. Kulish, “Expansions over the squared solutions and difference evolution equations,” J. Math. Phys., 25, 25–34 (1984).
N. M. Bogoliubov, R. K. Bullough, and G. D. Pang, “Exact solution of a q-boson hopping model,” Phys. Rev. B, 47, 11495–11498 (1993).
N. M. Bogoliubov and P. P. Kulish, “Exactly solvable models of quantum nonlinear optics,” Zap. Nauchn. Semin. POMI, 398, 26–54 (2012).
N. M. Bogoliubov and T. Nasar, “On the spectrum of the non-Hermitian phase-difference model,” Phys. Lett. A, 234, 345-350 (1997).
V. E. Korepin, “Calculations of norms of Bethe wave functions,” Commun. Math. Phys., 86, 391–418 (1982).
A. G. Izergin, “Partition function of the six-vertex model in a finite volume,” Dokl. Akad. Nauk SSSR, 297, 331–334 (1987).
A. G. Izergin, D. A. Coker, and V. E. Korepin, “Determinant formula for the six-vertex model,” J. Phys. A, 25, 4315–4334 (1992).
G. Kuperberg, “Another proof of the alternating-sign matrix conjecture,” Int. Res. Math. Notices, 1996, 139–150 (1996).
D. M. Bressoud, Proofs and Confirmations: The Story of the Alternating Sign Matrix Conjecture, Cambridge Univ. Press, Cambridge (1999).
N. M. Bogoliubov, “Boxed plane partitions as an exactly solvable boson model,” J. Phys. A, 38, 9415–9430 (2005).
N. M. Bogoliubov, “Four-vertex model and random tilings,” Teor. Mat. Fiz., 155, 25–38 (2008).
N. M. Bogoliubov and C. Malyshev, “Correlation functions of XX0 Heisenberg chain, q-binomial determinants, and random walks,” Nucl. Phys. B, 879, 268–291 (2014).
N. M. Bogoliubov, “Scalar products of vectors of states in totally asymmetric exactly solvable models on a ring,” Zap. Nauchn. Semin. POMI, 398, 5–25 (2012).
F. Colomo and A. G. Pronko, “The arctic curve of the domain-wall six-vertex model,” J. Stat. Phys., 138, 662–700 (2010).
F. Colomo and A. G. Pronko, “The limit shape of large alternating-sign matrices,” SIAM J. Discrete Math., 24, 1558–1571 (2010).
F. Colomo and A. G. Pronko, “Third-order phase transition in random tilings,” Phys. Rev. E, 88, 042125 (2013).
F. Colomo and A. G. Pronko, “Thermodynamics of the six-vertex model in an L-shaped domain,” Comm. Math. Phys., 339, 699–728 (2015).
N. M. Bogoliubov, “Five-vertex model with fixed boundary conditions,” Algebra Analiz, 21, 58–78 (2009).
R. J. Baxter, Exactly Solved Models in Statistical Mechanics, Academic Press, San Diego, CA (1982).
G. E. Andrews, The Theory of Partitions, Addison-Wesley Publishing (1976).
V. S. Kapitonov and A. G. Pronko, “Five-vertex model and boxed plane partitions,” Zap. Nauchn. Semin. POMI, 360, 162–179 (2008).
V. S. Kapitonov and A. G. Pronko, “Weighted enumerations of boxed plane partitions and inhomogeneous five-vertex model,” Zap. Nauchn. Semin. POMI, 398, 125–144 (2012).
H. Cohn, M. Larsen, and J. Propp, “The shape of a typical boxed plane partition,” New York J. Math., 4, 137–165 (1998).
I. G. Macdonald, Symmetric Functions and Hall Polynomials, 2nd ed., Oxford Univ. Press, Oxford (1995).
A. G. Pronko, “On the emptiness formation probability in the free-fermion six-vertex model with domain wall boundary conditions,” Zap. Nauchn. Semin. POMI, 398, 179–208 (2012).
A. Erdelyi, Higher Transcendental Functions, Vol. 1, McGraw-Hill, New York (1953).
K. Okamoto, “Studies on the Painlevé equations. I. Sixth Painlevé equation PVI,” Ann. Mat. Pura Appl., 146, 337–381 (1987).
P. J. Forrester and N. S. Witte, “Application of the τ -function theory of Painlevé equations to random matrices: PVI, the JUE, CyUE, cJUE and scaled limits,” Nagoya Math. J., 174, 29–114 (2004).
Author information
Authors and Affiliations
Corresponding author
Additional information
Dedicated to Petr Petrovich Kulish in connection with his 70th birthday
Translated from Zapiski Nauchnykh Seminarov POMI, Vol. 433, 2015, pp. 204–223.
Rights and permissions
About this article
Cite this article
Pronko, A.G. The Five-Vertex Model and Enumerations of Plane Partitions. J Math Sci 213, 756–768 (2016). https://doi.org/10.1007/s10958-016-2737-x
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10958-016-2737-x