Skip to main content
SpringerLink
Log in

Antiplane deformation by concentrated factors of bounded bodies with cracks and rigid inclusions

  • Published:
Journal of Mathematical Sciences Aims and scope Submit manuscript

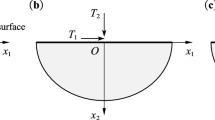
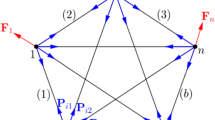
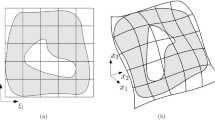
We propose two approaches to the solution of problems of antiplane deformation of bounded bodies with thin-walled defects by concentrated factors. The first is a numerical approach based on the boundary element method, in which the Volterra approach was developed to take into account the action of screw dislocations, and special tip boundary elements were introduced to determine the stress intensity factors. The second is an analytic-numerical method of direct full cutting, in which bounded bodies are modeled by using a space with a system of inhomogeneities contacting with each other, and, at the contact points, certain a priori unknown concentrated forces and dislocations act, which enables us to increase substantially the accuracy of computations for a small size of the resultant system of equation. Specific numerical examples for a body (bar) with a square cross-section containing a strip crack or rigid inclusion under the action of concentrated forces and screw dislocations have been considered.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. V. V. Bozhydarnyk and H. T. Sulym, Elements of the Theory of Plasticity and Strength [in Ukrainian], Svit, Lviv (1999).

  2. V. V. Bozhydarnyk and H. T. Sulym, Elements of the Theory of Elasticity [in Ukrainian], Svit, Lviv (1994).

  3. K. V. Vasil’ev and H. T. Sulym, “Direct cutting method for simulating the stress-strain state of isotropic layered environments with thin inhomogeneities under antiplane deformation,” Mashynoznavstvo, No. 11–12, 10–17 (2006).

  4. K. V. Vasil’ev and H. T. Sulym, “Solution of integral equations of problems of layered environments with arbitrary oriented strip inhomogeneities by the collocation method,” Visn. L’viv. Univ., Ser. Prykl. Mat. Informat., Issue 15, 157–169 (2009).

  5. K. Vasil’ev, Ya. Pasternak, and H. Sulym, “Antiplane deformation of a body square in plan with an internal thin inhomogeneity,” Visn. L’viv. Univ., Ser. Mekh.-Mat., Issue 73, 165–176 (2010).

  6. V. V. Panasyuk, Mechanics of Quasibrittle Fracture of Materials [in Russian], Naukova Dumka, Kiev (1991).

    Google Scholar 

  7. M. P. Savruk and A. M. Osechko, “Longitudinal shear of an infinite body with a system of polygonal cracks,” Fiz.-Khim. Mekh. Mater., 39, No. 5, 49–58 (2003); English translation: Mater. Sci., 39, No. 5, 658–671 (2003).

    Google Scholar 

  8. G. T. Sulym, “Antiplane problem for a system of linear inclusions in an isotropic environment,” Prikl. Mat. Mekh., 45, No. 2, 308–318 (1981).

    Google Scholar 

  9. H. T. Sulym, Fundamentals of the Mathematical Theory of Thermoelastic Equilibrium of Deformable Solid Bodies with Thin Inclusions [in Ukrainian], NTSh, Lviv (2007).

  10. E. E. Gdoutos, “Failure of a composite with a rigid fiber inclusion,” Acta Mech., 39, No. 3–4, 251–262 (1981).

    Article  Google Scholar 

  11. E. E. Gdoutos, Fracture Mechanics, Springer, Dordrecht (2005).

    MATH  Google Scholar 

  12. E. Pan and B. Amadei, “Fracture mechanics analysis of 2D anisotropic media with a new formulation of the boundary element method,” Int. J. Fracture, 77, 161–174 (1996).

    Article  Google Scholar 

  13. Ia. Pasternak, “Coupled 2D electric and mechanical fields in piezoelectric solids containing cracks and thin inhomogeneities,” Eng. Anal. Bound. Elem., 35, No. 4, 678–690 (2011).

    Article  MathSciNet  MATH  Google Scholar 

  14. Ia. M. Pasternak and H. T. Sulym, “Thin inclusions theory integral equations numerical solution using the boundary element method procedure,” in: Proc. of the Int. Conf. “Integral Equations–2010” (August 25–27, 2010, Lviv), PAIS, Lviv (2010), pp. 104–108.

  15. A. Portela, M. H. Aliabadi, and D. P. Rooke, “The dual boundary element method: effective implementation for crack problems,” Int. J. Numer. Meth. Eng., 33, 1269–1287 (1992).

    Article  MATH  Google Scholar 

  16. W. Wei-Liang, “Dual boundary element method applied to antiplane crack problems,” Math. Probl. Eng., ID 132980 (2009); doi: 10.1155/2009/132980.

  17. X. S. Zhang, “A tearing mode crack located anywhere in a finite rectangular sheet,” Eng. Fract. Mech., 33, No. 4, 509–516 (1989).

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Lutsk National Technical University, Lutsk, Ukraine

    Ia. M. Pasternak

  2. Pidstryhach Institute for Applied Problems of Mechanics and Mathematics, Ukrainian National Academy of Sciences, Lviv, Ukraine

    K. V. Vasil’ev & H. T. Sulym

  3. Franko Lviv National University, Lviv, Ukraine

    H. T. Sulym

Authors
  1. Ia. M. Pasternak
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. K. V. Vasil’ev
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. H. T. Sulym
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

Translated from Matematychni Metody ta Fizyko-Mekhanichni Polya, Vol. 55, No. 1, pp. 72–83, January–March, 2012.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Pasternak, I.M., Vasil’ev, K.V. & Sulym, H.T. Antiplane deformation by concentrated factors of bounded bodies with cracks and rigid inclusions. J Math Sci 190, 710–724 (2013). https://doi.org/10.1007/s10958-013-1282-0

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10958-013-1282-0

Keywords

Search

Navigation