Skip to main content
SpringerLink
Log in

Justification of the fast multipole method for the stokes system in the case of the interior diriclet problem

  • Published:
Journal of Mathematical Sciences Aims and scope Submit manuscript

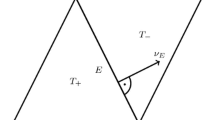
We provide all necessary theoretical statements concerning the hydrodynamical double layer potential, which enable the application of an adaptive version of the fast multipole method of Greengard and Rokhlin to the interior Dirichlet problem of the Stokes system and present numerical experiments confirming these theoretical statements. Bibliography: 26 titles. Illustrations: 3 figures.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. J. Carrier, L. Greengard, and V. Rokhlin, “A fast adaptive multipole algorithm for particle simulations,” SIAM J. Sci. Statist. Comput. 9, No. 4, 669–686 (1988).

    Article  MathSciNet  MATH  Google Scholar 

  2. F. Ethridge and L. Greengard, “A new fast multipole accelerated Poisson solver in two dimensions,” SIAM J. Sci. Comput. 23, No. 3, 741–760 (2001).

    Article  MathSciNet  MATH  Google Scholar 

  3. L. Greengard and V. Rokhlin, “The rapid evaluation of potential fields in three dimensions,” In: Vortex Methods, 121–141, Lect. Notes Math. 1360, Springer, Berlin (1988).

    Chapter  Google Scholar 

  4. L. Greengard and V. Rokhlin, “A new version of the fast multipole method for the Laplace equation in three dimensions,” Acta Numerica 6, 229 (1997).

    Article  MathSciNet  Google Scholar 

  5. R. Coifman, V. Rokhlin, and S. Wandzur, “The fast multipole method for the wave equation,” A pedestrian prescription, IEEE Antennas and Propagation Magazine (1993).

  6. M. Fischer, U. Gauger, and L. Gaul, “A multipole Galerkin boundary element method for acoustics,” Eng. Anal. Bound. Elem. 28, 155–162 (2004).

    Article  MATH  Google Scholar 

  7. L. Greengard, V. Rokhlin, et al. “Accelerating fast multipole methods for the Helmholz equation at low frequencies,” Comp. Sci. Eng. 5, 32–38 (1998).

    Google Scholar 

  8. L. Greengard, V. Rokhlin, et al. “A wideband fast multipole method for the Helmholz equation in three dimensions,” J. Comp. Phys. 216, 300–325 (2007).

    MathSciNet  Google Scholar 

  9. E. Darve, “The fast multipole method I: error analysis and asymptotic complexity,” SIAM J. Numer. Anal. 38 , 98–128 (2000).

    Article  MathSciNet  MATH  Google Scholar 

  10. E. Darve, “The fast multipole method: numerical implementation,” J. Comp. Phys. 160 , 195–240 (2000).

    Article  MathSciNet  MATH  Google Scholar 

  11. J.-M. Song and W. C. Chew, “Multilevel fast multipole algorithm for electromagnetic scattering by large complex objects,” IEEE Trans. Antennas Propag. textbf45(10) 1488–1496 (1997).

    Article  Google Scholar 

  12. G. Of, “A fast multipole boundary element method for the symmetric boundary integral formulation in linear elastostatics,” Comp. Fluid Solid Mech. 540–543 (2003).

  13. G. Of, O. Steinbach, and W. Wendland, “Application of a fast multipole Galerkin boundary element method in linear elastostatics,” Comput. Visual. Sci. 8, 201–209 (2005).

    Article  MathSciNet  Google Scholar 

  14. Y. Zhenhan, W. Haitao, W. Pengbo, and L. Ting, Some Applications of Fast Multipole Boundary Element Method, Preprint, Tsinghua University, Beijing (2004).

  15. G. C. Hsiao, “Integral representation of solutions for two-dimensional viscous flow problems,” Integral Equ. Operator Theory 5, 533–547 (1982).

    Article  MATH  Google Scholar 

  16. G. C. Hsiao and R. Kress, “On an integral equation for the two-dimensional exterior Stokes problem,” Appl. Numer. Math. 1, No. 1, 77–93 (1985).

    Article  MathSciNet  MATH  Google Scholar 

  17. M. Kohr and W. Wendland, “Variational boundary integral equations for the Stokes system,” Appl. Anal. 85, No. 1,, 1343–1372 (2006).

    Article  MathSciNet  MATH  Google Scholar 

  18. O. A. Ladyzhenskaya, The Mathematical Theory of Viscous Incompressible Flow, Gordon and Breach, New York (1969).

    MATH  Google Scholar 

  19. F. K. G. Odquist, “Über die Randwertaufgaben in der Hydrodynamik zäher Flüssigkeiten,” Math. Z. 32, 329–375 (1930).

    Article  MathSciNet  MATH  Google Scholar 

  20. W. Varnhorn, The Stokes Equations, Akademie-Verlag, Berlin (1994).

    MATH  Google Scholar 

  21. L. Greengard, M. C. Kropinski, and A. Mayo, “Integral equation methods for Stokes flow and isotropic elasticity in the plane,” J. Comp. Phys. 125, 403–414 (1996).

    Article  MathSciNet  MATH  Google Scholar 

  22. J. Gomez B. Peault et al. “A multipole direct and indirect BEM for 2D cavity flow at low Reynolds number,” Eng. Anal. Boundary Elem. 19, 17–31 (1997).

    Article  Google Scholar 

  23. B. N. Khoromskij and G. Wittum, Numerical Solution of Elliptic Differential Equations by Reduction to the Interface, Springer, Berlin (2004).

    MATH  Google Scholar 

  24. A. N. Popov, “Application of potential theory to the solution of a Linearized System of Navier–Stokes Equations in the two-dimensional case,” In: Proceedings of the Steklov Institute of Mathematics 116, pp. 167–186, Am. Math. Soc., Providence, RI (1973).

    Google Scholar 

  25. L. Greengard and V. Rokhlin, “A fast algorithm for particle simulations,” J. Comp. Phys. 135, 280–292 (1997).

    Article  MathSciNet  MATH  Google Scholar 

  26. V. Rokhlin, “Rapid solution of integral equations of classical potential theory,” J. Comp. Phys. 60, 187 (1985).

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Institute of Mathematics, Zurich University, 190, Winterthurerstrasse, Zurich, CH-8057, Switzerland

    T. Samrowski

Authors
  1. T. Samrowski
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to T. Samrowski.

Additional information

Translated from Problems in Mathematical Analysis 60, September 2011, pp. 65–76.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Samrowski, T. Justification of the fast multipole method for the stokes system in the case of the interior diriclet problem. J Math Sci 178, 637–650 (2011). https://doi.org/10.1007/s10958-011-0575-4

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10958-011-0575-4

Keywords

Search

Navigation