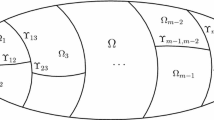
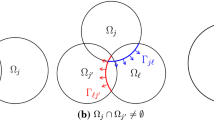
Based on the variational formulation and penalty method, we have considered the Neumann parallel scheme of the domain decomposition method for the solution of problems of one-sided contact between three-dimensional elastic bodies. We have shown the existence and uniqueness of a solution of the variational problem with penalty and convergence in the penalty parameter. The convergence of this scheme has been proved, and the optimal value of iteration parameter has been determined.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
R. Glowinski, J. L. Lions, and R. Tremolières, Numerical Analysis of Variational Inequalities [Russian translation], Mir, Moscow (1979).
A. Ya. Grigorenko, I. I. Dyyak, and I. I. Prokopyshin, “Domain decomposition methods for the solution of problems of frictionless contact between multilayer elastic bodies,” Prikl. Mekh. (to be published).
A. S. Kravchuk, “Statement of the problem of contact between several deformable bodies as a problem of nonlinear programming,” Prikl. Mat. Mekh., 42, No. 3, 467–473 (1978).
V. I. Kuz’menko, “On the variational approach to the theory of contact problems for nonlinearly-elastic layered bodies,” Prikl. Mat. Mekh., 43, No. 5, 893–901 (1979).
J. L. Lions, Some Methods for the Solution of Nonlinear Boundary-Value Problems [Russian translation], Mir, Moscow (1972).
I. I. Vorovich and V. M. Aleksandrov (editors), Mechanics of Contact Interactions [in Russian], Fizmatlit, Moscow (2001).
I. Prokopyshyn, “Parallel schemes of the domain decomposition method for contact problems of the theory of elasticity without friction,” in: Bulletin of the Lviv University, Ser. “Applied Mathematics and Informatics” [in Ukrainian], Issue 14 (2008), pp. 123–133.
K. Rektorys, Variational Methods in Mathematics, Science and Engineering [Russian translation], Mir, Moscow (1985).
J. Céa, Optimization. Theory and Algorithms [Russian translation], Mir, Moscow (1973).
P. Avery and C. Farhat, “The FETI family of domain decomposition methods for inequality-constrained quadratic programming: Application to contact problems with conforming and nonconforming interfaces,” Comput. Meth. Appl. Mech. Eng., 198, 1673–1683 (2009).
G. Bayada, J. Sabil, and T. Sassi, “A Neumann–Neumann domain decomposition algorithm for the Signorini problem,” Appl. Math. Lett., 17, No. 10, 1153–1159 (2004).
J. Daněk, “Domain decomposition method for contact problems with small range contact,” J. Math. Comput. Simulation, 61, No. 3–6, 359–373 (2003).
C. Eck and B. I. Wohlmuth, “Convergence of contact–Neumann iteration for solution of two-body contact problems,” Math. Models Meth. Appl. Sci., 13, No. 7, 1103–1118 (2003).
S. Hueber and B. I. Wohlmuth, “A primal-dual active set strategy for non-linear multibody contact problems,” Comput. Meth. Appl. Mech. Eng., 194, 3147–3166 (2005).
A. M. Khludnev and V. A. Kovtunenko, Analysis of Cracks in Solids, WIT Press, Southampton (2000).
N. Kikuchi and J. T. Oden, Contact Problem in Elasticity: A Study of Variational Inequalities and Finite Element Methods, SIAM, Philadelphia (1988).
R. Krause and B. Wohlmuth, “A Dirichlet–Neumann type algorithm for contact problems with friction,” Comput. Visual. Sci., 5, No. 3, 139–148 (2002).
P. Wriggers, Computational Contact Mechanics, Springer (2006).
Author information
Authors and Affiliations
Additional information
Translated from Matematychni Metody ta Fizyko-Mekhanichni Polya, Vol. 52, No. 3, pp. 78–89, July–September, 2009.
Rights and permissions
About this article
Cite this article
Dyyak, I.I., Prokopyshyn, I.I. Convergence of the Neumann parallel scheme of the domain decomposition method for problems of frictionless contact between several elastic bodies. J Math Sci 171, 516–533 (2010). https://doi.org/10.1007/s10958-010-0154-0
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10958-010-0154-0