Connecting measures by means of branched transportation networks at finite cost

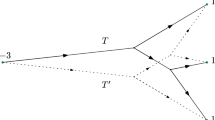
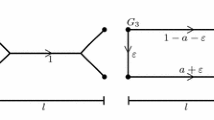
We study the couples finite Borel measures φ ₀ and φ ₁ with compact support in $\mathbb{R}^n$ which can be transported to each other at a finite W ^α cost, where

$$ W^{\alpha } \left( {\varphi_0, \varphi_1 } \right): = \inf \left\{ {\mathbb{M}^{\alpha} \left( T \right):\partial T = \varphi_0 - \varphi_1} \right\},\quad \alpha \in \left[ {0,1} \right], $$

the infimum is taken over real normal currents of finite mass and $\mathbb{M}^{\alpha } \left( T \right)$ denotes the α-mass of T. Besides the class of α-irrigable measures (i.e., measures which can be transported to a Dirac measure with the appropriate total mass at a finite W ^α cost), two other important classes of measures are studied, which are called in the paper purely α-nonirrigable and marginally α-nonirrigable and are in a certain sense complementary to each other. For instance, purely α-nonirrigable and Ahlfors-regular measures are, roughly speaking, those having sufficiently high dimension. One shows that for φ ₀ to be transported to φ ₁ at finite W ^α cost their naturally defined purely α-nonirrigable parts have to coincide. Bibliography: 19 titles.