Abstract
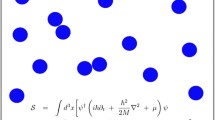
We consider a quantum field-theoretical model which describes spatially-nonhomogeneous, one-dimensional, repulsive Bose gas in an external harmonic potential. The two-point correlation function is calculated in the framework of functional integration. The corresponding functional integrals are estimated by means of stationary phase approximation. Asymptotic estimates are obtained in the limit as the temperature tends to zero while the volume occupied by the quasi-condensate increases. A power-law behavior is established for the correlation function in this limit. It is shown that the power-law behavior is governed by the critical exponent depending on spatial arguments. Bibliography 32 titles.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
F. Dalfovo, S. Giorgini, L. P. Pitaevskii, and S. Stringari, Rev. Mod. Phys., 71, 463 (1999).
C. J. Pethic and H. Smith, Bose-Einstein Condensation in Dilute Gases, Cambridge Univ. Press (2002).
T. Donner, S. Ritter, T. Bourdel, A. Öttl, M. Köhl, and T. Esslinger, Science, 315, 1556 (2007).
D. M. Gangardt and G. V. Shlyapnikov, Phys. Rev. Lett., 90, 010401 (2003).
K. V. Kheruntsyan, D. M. Gangardt, P. D. Drummond, and G. V. Shlyapnikov, Phys. Rev. A, 71, 053615 (2005).
C. Gils, L. Pollet, A. Vernier, F. Herbert, G. G. Batrouni, and M. Troyer, “Quantum Monte-Carlo study of a 1D phase-fluctuating condensate,” arXiv:cond-mat/0701441 (2007).
V. E. Korepin, N. M. Bogoliubov, and A. G. Izergin, Quantum Inverse Scattering Method and Correlation Functions, Cambridge Univ. Press (1993).
N. M. Bogoliubov, R. K. Bullough, V. S. Kapitonov, C. Malyshev, and J. Timonen, Europhys. Lett., 55, 755 (2001).
N. M. Bogoliubov, C. Malyshev, R. K. Bullough, and J. Timonen, Phys. Rev. A, 69, 023619 (2004).
N. M. Bogoliubov and C. Malyshev, St.Petersburg Math. J., 17, 63 (2006).
V. N. Popov, Functional Integrals in Quantum Field Theory and Statistical Physics, D. Reidel, Dordrecht (1983).
L. S. Schulman, Techniques and Applications of Path Integration, J. Wiley & Sons, New York (1981).
V. N. Popov, Functional Integrals and Collective Excitations, Cambridge Univ. Press (1987, 1990).
V. N. Popov and V. S. Yarunin, Collective Effects in Quantum Statistics of Radiation and Matter, Kluwer, Dordrecht (1988).
H. Kleinert, Path Integrals in Quantum Mechanics, Statistics, Polymer Physics, and Financial Markets, World Scientific, Singapore (1990, 1995, 2004).
V. N. Popov, J. Soviet Math., 46, 1619 (1989).
C. Itzykson and J.-B. Zuber, Quantum Field Theory, McGraw-Hill, New York (1980).
M. Naraschewski and D. M. Stamper-Kurn, Phys. Rev. A, 58, 2423 (1998).
S. Stringari, Phys. Rev. A, 58, 2385 (1998).
V. N. Popov, Teor. Mat. Fiz., 11, 354 (1972).
A. Erdélyi, W. Magnus, F. Oberhettinger, and F. G. Tricomi, Higher Transcendental Functions, McGraw-Hill, New York (1953).
E. Elizalde and A. Romeo, Rev. Math. Phys., 1, 113 (1989).
P. Di Francesco, P. Mathieu, and D. Sénéchal, Conformal Field Theory, Springer, New York (1997).
E. W. Hobson, The Theory of Spherical and Ellipsoidal Harmonics, Cambridge Univ. Press (1931).
Author information
Authors and Affiliations
Corresponding author
Additional information
__________
Translated from Zapiski Nauchnykh Seminarov POMI, Vol. 347, 2007, pp. 56–74.
Rights and permissions
About this article
Cite this article
Bogoliubov, N.M., Malyshev, C. Calculation of the asymptotics of the two-point correlation function for one-dimensional Bose gas. J Math Sci 151, 2829–2839 (2008). https://doi.org/10.1007/s10958-008-9001-y
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10958-008-9001-y