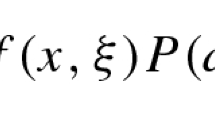Skip to main content
SpringerLink
Log in

Sequential Importance Sampling Algorithms for Dynamic Stochastic Programming

  • Published:
Journal of Mathematical Sciences Aims and scope Submit manuscript

Abstract

This paper gives a comprehensive treatment of EVPI-based sequential importance sampling algorithms for dynamic (multistage) stochastic programming problems. Both theory and computational algorithms are discussed. Under general assumptions it is shown that both an expected value of perfect information (EVPI) process and the corresponding marginal EVPI process (the supremum norm of the conditional expectation of its generalized derivative) are nonanticipative nonnegative supermartingales. These processes are used as importance criteria in the class of sampling algorithms treated in the paper. When their values are negligible at a node of the current sample problem scenario tree, scenarios descending from the node are replaced by a single scenario at the next iteration. On the other hand, high values lead to increasing the number of scenarios descending from the node. Both the small sample and asymptotic properties of the sample problem estimates arising from the algorithms are established, and the former are evaluated numerically in the context of a financial planning problem. Finally, current and future research is described. Bibliography: 49 titles.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

REFERENCES

  1. K. Back and S. R. Pliska, “The shadow price of information in continuous-time decision problems,” Stochastics, 22, 151–186 (1987).

    MathSciNet  Google Scholar 

  2. B. Bereanu, “On stochastic linear programming II: Distribution problems. Non-stochastic technology matrix,” Rev. Roumaine Math. Pures Appl., 11, 713–725 (1966).

    MATH  MathSciNet  Google Scholar 

  3. B. Bereanu, “On stochastic linear programming: Distribution problems. Stochastic technology matrix,” Z. Wahrscheinlichkeitstheor. Verw. Geb., 8, 148–152 (1967).

    Article  MATH  MathSciNet  Google Scholar 

  4. P. Billingsley, Probability and Measure, 2nd edition, Wiley, New York (1980).

    Google Scholar 

  5. J. R. Birge, M. A. H. Dempster, H. I. Gassmann, E. A. Gunn, A. J. King, and S. Wallace, “A standard input format for multiperiod stochastic linear programs,” Committee on Algorithms Newsletter, 17, 1–20 (1987).

    Google Scholar 

  6. M. J. Brennan, E. S. Schwartz, and R. Lagnado, “Strategic asset allocation,” J. Econom. Dynam. Control, 21, 1377–1403 (1997).

    Article  MathSciNet  Google Scholar 

  7. Z. Chen, G. Consigli, M. A. H. Dempster, and N. Hicks Pedron, “Towards sequential sampling algorithms for dynamic portfolio management,” in: [49], pp. 197–211.

  8. X. Corvera Poire, Model Generation and Sampling Algorithms for Dynamic Stochastic Programming. Ph.D. Thesis, Department of Mathematics, University of Essex (1995).

  9. X. Corvera Poire, STOCHGEN User's Manual, Department of Mathematics, University of Essex (1995).

  10. J. W. Daniel, The Approximate Minimization of Functionals, Prentice-Hall, Englewood Cliffs, New Jersey (1971).

    Google Scholar 

  11. G. B. Dantzig and P. W. Glynn, “Parallel processors for planning under uncertainty,” Ann. Oper. Res., 22, 1–21 (1990).

    Article  MathSciNet  Google Scholar 

  12. G. B. Dantzig and G. Infanger, “Large-scale stochastic linear programs: Importance sampling and Benders decomposition,” Technical Report SOL 91-4, Department of Operations Research, Stanford University, Stanford, California (1991).

    Google Scholar 

  13. G. B. Dantzig and A. Madansky, “On the solution of two-stage linear programs under uncertainty,” in: Proceedings of the Fourth Symposium on Mathematical Statistics and Probability, Vol. I, University of California, Berkeley (1961), pp. 165–176.

    Google Scholar 

  14. M. H. A. Davis, M. A. H. Dempster, and R. J. Elliott, “On the value of information in controlled diffusion processes,” in: [33], pp. 125–138.

  15. M. A. H. Dempster (ed.), Stochastic Programming, Academic Press, London (1980).

    Google Scholar 

  16. M. A. H. Dempster, “The expected value of perfect information in the optimal evolution of stochastic systems,” in: Stochastic Differential Systems, M. Arato, D. Vermes, and A. V. Balikrishnan (eds.), Springer, Berlin (1981), pp. 25–40.

    Google Scholar 

  17. M. A. H. Dempster, “On stochastic programming: II. Dynamic problems under risk,” Stochastics, 25, 15–42 (1988).

    MATH  MathSciNet  Google Scholar 

  18. M. A. H. Dempster and R. T. Thompson, “EVPI-based importance sampling solution procedures for multistage stochastic linear programmes on parallel MIMD architectures,” Ann. Oper. Res., 90, 161–184 (1999).

    Article  MathSciNet  Google Scholar 

  19. D. Dentcheva and W. Romisch, “Differential stability of two-stage stochastic programs,” Preprint No. 96-36, Institute of Mathematics, Humboldt University, Berlin (1996).

    Google Scholar 

  20. O. Fiedler and W. Romisch, “Stability in multistage stochastic programming,” Ann. Oper. Res., 56, 79–93 (1995).

    Article  MathSciNet  Google Scholar 

  21. H. I. Gassmann, “MSLiP: A computer code for the multistage stochastic linear programming problem,” Math. Program., 47, 407–423 (1990).

    Article  MATH  MathSciNet  Google Scholar 

  22. N. Hicks Pedron, Model-Based Asset Management: A Comparative Study, Ph.D. Thesis, Judge Institute of Management Studies, University of Cambridge (1998).

  23. J. L. Higle and S. Sen, “Stochastic decomposition: An algorithm for two stage linear programs with recourse,” Math. Oper. Res., 16, 650–669 (1991).

    MathSciNet  Google Scholar 

  24. J. L. Higle and S. Sen, Stochastic Decomposition: A Statistical Method for Large Scale Stochastic Linear Programming, Kluwer Academic Publishers, Dordrecht (1996).

    Google Scholar 

  25. G. Infanger, Planning under Uncertainty: Solving Large-Scale Stochastic Linear Programs, Boyd & Fraser, Danvers, Massachusetts (1994).

    Google Scholar 

  26. A. J. King, Asymptotic Behaviour of Solutions in Stochastic Optimization: Nonsmooth Analysis and the Derivation of Non-Normal Limit Distributions, Ph.D. Thesis, Department of Mathematics, University of Washington (1986).

  27. A. J. King, “Generalized delta theorems for multivalued mappings and measurable selections,” Math. Oper. Res., 14, 720–736 (1989).

    MATH  MathSciNet  Google Scholar 

  28. A. J. King, “Martingales and duality in contingent claims analysis: The discrete case,” Research Report RC21153, IBM Research Division, T. J. Watson Research Center, Yorktown Heights, New York (1998).

    Google Scholar 

  29. A. J. King and R. T. Rockafellar, “Asymptotic theory for solutions in statistical estimation and stochastic programming,” Math. Oper. Res., 18, 148–162 (1993).

    MathSciNet  Google Scholar 

  30. M. Lane and P. Hutchinson, “A model for managing a certificate of deposit portfolio under uncertainty,” in: [15], pp. 473–493.

  31. W. K. Mak, D. P. Morton, and R. K. Wood, “Monte Carlo bounding techniques for determining solution quality in stochastic programs,” Research Report, Department of Computer Science, University of Texas at Austin (1997).

  32. H. M. Markowitz, Portfolio Selection, Efficient Diversification of Investments, 2nd edition, Blackwell, Oxford (1987).

    Google Scholar 

  33. E. Mayer-Wolf, E. Merzbach, and A. Schwartz, Stochastic Analysis, Academic Press, New York (1991).

    Google Scholar 

  34. V. I. Norkin, G. C. Pflug, and A. Ruszcynski, “A branch and bound method for stochastic global optimization,” Working Paper WP-96-065, International Institute for Applied Systems Analysis, Laxenburg, Austria (1996).

    Google Scholar 

  35. P. Olsen, “Discretizations of multistage stochastic programming problems,” Math. Program. Studies, 6, 111–124 (1976).

    MATH  MathSciNet  Google Scholar 

  36. G. Ch. Pflug, Optimization of Stochastic Models: The Interface Between Simulation and Optimization, Kluwer, Boston (1996).

    Google Scholar 

  37. A. Prekopa, “Laws of large numbers for random linear programs,” Math. Systems Theory, 6, 277–288 (1972).

    MATH  MathSciNet  Google Scholar 

  38. S. T. Rachev, Probability Metrics and the Stability of Stochastic Models, Wiley, New York (1991).

    Google Scholar 

  39. H. Raiffa, Decision Analysis, Addison-Wesley, Reading, Massachusetts (1968).

    Google Scholar 

  40. R. T. Rockafellar and R. J.-B. Wets, “Nonanticipativity and L1-martingales in stochastic optimization problems,” Math. Program. Studies, 6, 170–186 (1976).

    MathSciNet  Google Scholar 

  41. R. T. Rockafellar and R. J.-B. Wets, “A Lagrangian finite generation technique for solving linear-quadratic problems in stochastic programming,” Math. Program. Studies, 28, 63–93 (1986).

    MathSciNet  Google Scholar 

  42. W. Romisch, “Quantitative stability of stochastic programs,” Presented at 16th International Symposium on Mathematical Programming, Lausanne (1997).

  43. R. Y. Rubinstein and A. Shapiro, Discrete Event Systems: Sensitivity Analysis and Stochastic Optimization by the Score Function Method, Wiley, New York (1993).

    Google Scholar 

  44. G. Salinetti and R. J.-B. Wets, “On the distribution of measurable multifunctions (random sets), normal integrands, stochastic processes and stochastic infima,” Math. Oper. Res., 11, 385–419 (1986).

    MathSciNet  Google Scholar 

  45. A. Shapiro, “Asymptotic analysis of stochastic programs,” Ann. Oper. Res., 30, 169–186 (1991).

    Article  MATH  MathSciNet  Google Scholar 

  46. A. Shapiro, “Asymptotic behaviour of optimal solutions in stochastic programming,” Math. Oper. Res., 18, 829–845 (1993).

    MATH  MathSciNet  Google Scholar 

  47. A. Shapiro, “Simulation-based optimization: Convergence analysis and statistical inference,” Commun. Stat., Stochastic Models, 12, 425–454 (1996).

    MATH  Google Scholar 

  48. R. T. Thompson, MSLiP-OSL 8.3 User's Guide, Judge Institute of Management Studies, University of Cambridge (1997).

  49. C. Zopounidis (ed.), Operational Tools in the Management of Financial Risks, Kluwer, Dordrecht (1997).

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Centre for Financial Research, Judge Institute of Management Studies, University of Cambridge, Cambridge, UK

    M. A. H. Dempster

  2. Cambridge Systems Associates Limited, Cambridge, UK

    M. A. H. Dempster

Authors
  1. M. A. H. Dempster
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

__________

Published in Zapiski Nauchnykh Seminarov POMI, Vol. 312, 2004, pp. 94–129.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Dempster, M.A.H. Sequential Importance Sampling Algorithms for Dynamic Stochastic Programming. J Math Sci 133, 1422–1444 (2006). https://doi.org/10.1007/s10958-006-0058-1

Download citation

  • Received:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10958-006-0058-1

Keywords

Search

Navigation