Skip to main content
SpringerLink
Log in

A Strong Convergence Theorem for Solving an Equilibrium Problem and a Fixed Point Problem Using the Bregman Distance

  • Published:
Journal of Optimization Theory and Applications Aims and scope Submit manuscript

Abstract

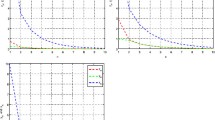
In this paper, using the Bregman distance, we introduce a new projection-type algorithm for finding a common element of the set of solutions of an equilibrium problem and the set of fixed points. Then the strong convergence of the sequence generated by the algorithm will be established under suitable conditions. Finally, using MATLAB software, we present a numerical example to illustrate the convergence performance of our algorithm.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1

Similar content being viewed by others

References

  1. Agarwal, R.P., O’Regan, D., Sahu, D.R.: Fixed Point Theory for Lipschitzian-Type Mappings With Applications, vol. 6. Springer, New York (2009)

    MATH  Google Scholar 

  2. Ambrosetti, A., Prodi, G.: A Primer of Nonlinear Analysis. Cambridge University Press, Cambridge (1993)

    MATH  Google Scholar 

  3. Anh, P.N.: A hybrid extragradient method for pseudomonotone equilibrium problems and fixed point problems. Bull. Malays. Math. Sci. Soc 36(1), 107–116 (2013)

    MATH  MathSciNet  Google Scholar 

  4. Bauschke, H.H., Borwein, J.M.: On projection algorithms for solving convex feasibility problems. SIAM Rev. 38, 367–426 (1996)

    Article  MATH  MathSciNet  Google Scholar 

  5. Bauschke, H.H., Borwein, J.M., Combettes, P.L.: Essential smoothness, essential strict convexity, and Legendre functions in Banach spaces. Commun. Contemp. Math. 3, 615–647 (2001)

    Article  MATH  MathSciNet  Google Scholar 

  6. Bregman, L.M.: A relaxation method for finding the common point of convex sets and its application to the solution of problems in convex programming. USSR Comput. Math. Math. Phys. 7, 200–217 (1967)

    Article  MathSciNet  Google Scholar 

  7. Bonnans, J.F., Shapiro, A.: Perturbation Analysis of Optimization Problems. Springer, New York (2000)

    Book  MATH  Google Scholar 

  8. Butnariu, D., Iusem, A.N., Zalinescu, C.: On uniform convexity, total convexity and convergence of the proximal point and outer Bregman projection algorithms in Banach spaces. J. Convex Anal. 10, 35–61 (2003)

    MATH  MathSciNet  Google Scholar 

  9. Butnariu, D., Iusem, A.N.: Totally Convex Functions for Fixed Points Computation and Infinite Dimensional Optimization. Kluwer Academic Publishers, Dordrecht (2000)

    Book  MATH  Google Scholar 

  10. Butnariu, D., Resmerita, E.: Bregman distances, totally convex functions and a method for solving operator equations in Banach spaces. Abstr. Appl. Anal. Art. ID 84919, 1–39 (2006)

    MATH  Google Scholar 

  11. Censor, Y., Reich, S.: Iterations of paracontractions and firmly nonexpansive operators with applications to feasibility and optimization. Optimization 37, 323–339 (1996)

    Article  MATH  MathSciNet  Google Scholar 

  12. Cioranescu, I.: Geometry of Banach Spaces, Duality Mappings and Nonlinear Problems. Kluwer Academic Publishers, Dordrecht (1990)

    Book  MATH  Google Scholar 

  13. Combettes, P.L., Hirstoaga, S.A.: Equilibrium programming in Hilbert spaces. J. Nonlinear Convex Anal. 6, 117–136 (2005)

    MATH  MathSciNet  Google Scholar 

  14. Eskandani, G.Z., Raeisi, M., Rassias, T.M.: A hybrid extragradient method for solving pseudomonotone equilibrium problems using Bregman distance. J. fixed point theory appl. 20, 132 (2018). https://doi.org/10.1007/s11784-018-0611-9

    Article  MATH  MathSciNet  Google Scholar 

  15. Hieu, D.V., Muu, L.D., Anh, P.K.: Parallel hybrid extragradient methods for pseudmonotone equilibrium problems and nonexpansive mappings. Numer. Algorithms 73, 197–217 (2016)

    Article  MATH  MathSciNet  Google Scholar 

  16. Hiriart-Urruty, J.-B., Lemarchal, C.: Grundlehren der mathematischen Wissenschaften 306. In Convex Analysis and Minimization Algorithms II. Springer, Berlin (1993)

  17. Hussain, A., Ali, D., Karapinar, E.: Stability data dependency and errors estimation for a general iteration method. Alex. Eng. J. 60, 703–710 (2021). https://doi.org/10.1016/j.aej.2020.10.002

    Article  Google Scholar 

  18. Jolaoso, L.O., Taiwo, A., Alakoya, T.O.: A strong convergence theorem for solving pseudo-monotone variational inequalities using projection methods. J. Optim. Theory Appl. 185, 744–766 (2020). https://doi.org/10.1007/s10957-020-01672-3

    Article  MATH  MathSciNet  Google Scholar 

  19. Kohsaka, F., Takahashi, W.: Proximal point algorithm with Bregman functions in Banach spaces. J. Nonlinear Convex Anal. 6, 505–523 (2005)

    MATH  MathSciNet  Google Scholar 

  20. Mainge, P.E.: Strong convergence of projected subgradient methods for nonsmooth and nonstrictly convex minimization. Set Val. Anal. 16, 899–912 (2008)

    Article  MATH  MathSciNet  Google Scholar 

  21. Marino, G., Scardamaglia, B., Karapinar, E.: Strong convergence theorem for strict pseudo-contractions in Hilbert spaces. J. Inequal. Appl. 2016, 134 (2016). https://doi.org/10.1186/s13660-016-1072-6

    Article  MATH  MathSciNet  Google Scholar 

  22. Naraghirad, E., Yao, J.C.: Bregman weak relatively nonexpansive mappings in Banach spaces. Fixed Point Theory Appl. (2013). https://doi.org/10.1186/1687-1812-2013-141

    Article  MATH  MathSciNet  Google Scholar 

  23. Reem, D., Reich, S., De Pierro, A.: Re-examination of Bregman functions and new properties of their divergences. Optimization 68, 279–348 (2019)

    Article  MATH  MathSciNet  Google Scholar 

  24. Reich, S.: A weak convergence theorem for the alternating method with Bregman distances. In: Kartsatos, A. (ed.) Theory and Applications of Nonlinear Operators of Accretive and Monotone Type, pp. 313–318. Marcel Dekker, NewYork (1996)

    Google Scholar 

  25. Reich, S., Sabach, S.: A strong convergence theorem for proximal type- algorithm in reflexive Banach spaces. J. Nonlinear Convex Anal. 10, 471–485 (2009)

    MATH  MathSciNet  Google Scholar 

  26. Reich, S., Sabach, S.: Two strong convergence theorems for Bregman strongly nonexpansive operators in reflexive Banach spaces. Nonlinear Anal. Theory Methods Appl. 73, 122–135 (2010)

    Article  MATH  MathSciNet  Google Scholar 

  27. Sabach, S.: Products of finitely many resolvents of maximal monotone mappings in reflexive banach spaces. SIAM J. Optim. 21, 1289–1308 (2011)

    Article  MATH  MathSciNet  Google Scholar 

  28. Shahzad, N., Zegeye, H.: Convergence theorem for common fixed points of a finite family of multi-valued Bregman relatively nonexpansive mappings. Fixed Point Theory Appl. (2014). https://doi.org/10.1186/1687-1812-2014-152

    Article  MATH  MathSciNet  Google Scholar 

  29. Tada, A., Takahashi, W.: Strong convergence theorem for an equilibrium problem and a nonexpansive mapping. In: Takahashi, W., Tanaka, T. (eds.) Nonlinear Analysis Convex Analysis. Yokohama Publishers, Yokohama (2006)

    Google Scholar 

  30. Takahashi, W.: Nonlinear Functional Analysis. Yokohama Publishers, Yokohama (2000)

    MATH  Google Scholar 

  31. Thong, D.V., Dung, V.T., Cho, Y.J.: A new strong convergence for solving split variational inclusion problems. Numer. Algor. 86, 565–591 (2021). https://doi.org/10.1007/s11075-020-00901-0

    Article  MATH  MathSciNet  Google Scholar 

  32. Tiel, J.V.: Convex Analysis: An Introductory Text. Wiley, New York (1984)

    MATH  Google Scholar 

  33. Xu, H.K.: Another control condition in an iterative method for nonexpansive mappings. Bull. Austral. Math. Soc 65, 109–113 (2002)

    Article  MATH  MathSciNet  Google Scholar 

  34. Yao, J.C.: Variational inequalities with generalized monotone operators. Math. Oper. Res. 19, 691–705 (1994)

    Article  MATH  MathSciNet  Google Scholar 

  35. Zălinescu, C.: Convex Analysis in General Vector Spaces. World Scientific Publishing, Singapore (2002)

    Book  MATH  Google Scholar 

  36. Zhao, X., K\(\ddot{\text{o}}\)bis, M.A., Yao, Y,: A projected subgradient method for nondifferentiable Quasiconvex multiobjective optimization problems. J. Optim. Theory Appl. (2021). https://doi.org/10.1007/s10957-021-01872-5

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Payame Noor University, P. O. Box 19395-4697, Tehran, Iran

    Mostafa Ghadampour

  2. Department of Mathematics, Lorestan University, Khoramabad, Lorestan, Iran

    Ebrahim Soori

  3. Department of Mathematics, Texas A &M University-Kingsville, 700 University Blvd., MSC 172, Kingsville, TX, USA

    Ravi P. Agarwal

  4. School of Mathematics, Statistics, National University of Ireland, Galway, Ireland

    Donal O’Regan

Authors
  1. Mostafa Ghadampour
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ebrahim Soori
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Ravi P. Agarwal
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Donal O’Regan
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ebrahim Soori.

Additional information

Communicated by Firdaus E. Udwadia.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ghadampour, M., Soori, E., Agarwal, R.P. et al. A Strong Convergence Theorem for Solving an Equilibrium Problem and a Fixed Point Problem Using the Bregman Distance. J Optim Theory Appl 195, 854–877 (2022). https://doi.org/10.1007/s10957-022-02110-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10957-022-02110-2

Keywords

Mathematics Subject Classification

Search

Navigation