Abstract
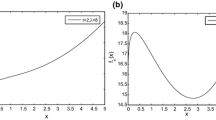
The matrix rank minimization problem is widely applied in many fields such as control, signal processing and system identification. However, the problem is NP-hard in general and is computationally hard to directly solve in practice. In this paper, we provide a new approximation function of the matrix rank function, and the corresponding approximation problems can be used to approximate the matrix rank minimization problem within any level of accuracy. Furthermore, the successive projected gradient method, which is designed based on the monotonicity and the Fréchet derivative of these new approximation function, can be used to solve the matrix rank minimization this problem by using the projected gradient method to find the stationary points of a series of approximation problems. Finally, the convergence analysis and the preliminary numerical results are given.
Similar content being viewed by others
References
Mesbahi, M., Papavassilopoulos, G.P.: On the rank minimization problem over a positive semidefinite linear matrix inequality. IEEE Trans. Autom. Control 42, 239–243 (1997)
Candès, E.J., Tao, T.: The power of convex relaxation: near-optimal matrix completion. IEEE Trans. Inf. Theory 56, 2053–2080 (2010)
Candès, E.J., Recht, B.: Exact matrix completion via convex optimization. Found. Comput. Math. 9, 712–772 (2009)
Amit, Y., Fink, M., Srebro, M., Ullman, S.: Uncovering shared structures in multiclass classification. In: Proceedings of the Twenty-fourth International Conference on Machine Learning (2007)
Trosset, M.W.: Distance matrix completion by numerical optimization. Comput. Optim. Appl. 17, 11–22 (2000)
Linial, N., London, E., Rabinovich, Y.: The geometry of graphs and some of its algorithmic applications. Combinatorica 15, 215–245 (1995)
Dattorro, J.: In: Convex Optimization and Euclidean Distance Geometry. MEBOO (2009)
Ames, B., Vavasis, S.: Nuclear norm minimization for the planted clique and biclique problems. Technical Report, University of Waterloo, Canada (2009)
Sun, W.Y., Yuan, Y.X.: Optimization Theory and Methods: Nonlinear Programming. Springer, Berlin (2006)
Zhao, Y.B., Fukushima, M.: Rank-one solutions for homogeneous linear matrix equations over the positive semidefinite cone. Technical Report, University of Birmingham (2010)
Candès, E.J., Romberg, J., Tao, T.: Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information. IEEE Trans. Inf. Theory 52, 489–509 (2006)
Recht, B., Fazel, M., Parrilo, P.A.: Guaranteed minimum-rank solutions of linear matrix equations via nuclear norm minimization. SIAM Rev. 52, 471–501 (2010)
Fazel, M.: Matrix rank minimization with applications. PhD Thesis, Stanford University (2002)
Lu, Z., Monteiro, R.D.C., Yuan, M.: Convex optimization methods for dimension reduction and coefficient estimation in multivariate linear regression. Preprint (2009). arXiv:0904.0691
Ma, S.Q., Goldfarb, D., Chen, L.F.: Fixed point and Bregman iterative methods for matrix rank minimization. Math. Program. 128, 321–353 (2011)
Zhao, Y.B.: Approximation theory of matrix rank minimization and its application to quadratic equations. Linear Algebra Appl. 437, 77–93 (2012)
Bi, S.J., Pan, S.H.: Approximation of rank function and its application to the nearest low-rank correlation matrix. Optimization Online (2011). http://www.optimization-online.org/DB-FILE/2011/07/3094.pdf
Sun, D.F., Sun, J.: Semismooth matrix-valued functions. Math. Oper. Res. 27, 150–169 (2002)
Tseng, P.: Merit functions for semi-definite complementarity problems. Math. Program. 83, 159–185 (1998)
Sun, D.F.: The strong second order sufficient condition and constraint nondegeneracy in nonlinear semidefinite programming and their implications. Math. Oper. Res. 31, 761–776 (2006)
Goldstein, A.A.: Convex programming in Hilbert space. Bull. Am. Math. Soc. 7(0), 709–710 (1964)
Levitin, E.S., Polyak, B.T.: Constrained minimization problems. USSR J. Comput. Math. Phys. 6, 1–50 (1966)
Calamai, P.H., More, J.J.: Projected gradient methods for linearly constrained problems. Math. Program. 39, 93–116 (1987)
Dunn, J.C.: Global and asymptotic convergence rate estimates for a class of projected gradient processes. SIAM J. Control Optim. 19, 368–400 (1981)
Zhang, C., Chen, X.J.: Smoothing projected gradient method and its application to stochastic linear complementarity problems. SIAM J. Optim. 20, 627–649 (2009)
Helmberg, C.: Semidefinite programming for combinatorial optimization. Semidefinite programming home page (2000). http://www.zib.de/helmberg/semidef.html
Liu, Y.J., Sun, D.F., Toh, K.C.: An implementable proximal point algorithmic framework for nuclear norm minimization. Math. Program. 133, 399–436 (2012)
Acknowledgements
This work was supported by the National Natural Science Foundations of China (11301080, 11071041, 11171159), the Foundation of the Education Department of Fujian Province (JB12040) and the Project of Nonlinear analysis and its applications (IRTL1206).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Li, C. A New Approximation of the Matrix Rank Function and Its Application to Matrix Rank Minimization. J Optim Theory Appl 163, 569–594 (2014). https://doi.org/10.1007/s10957-013-0477-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10957-013-0477-3