Skip to main content
SpringerLink
Log in

Projected Subgradient Minimization Versus Superiorization

  • Published:
Journal of Optimization Theory and Applications Aims and scope Submit manuscript

Abstract

The projected subgradient method for constrained minimization repeatedly interlaces subgradient steps for the objective function with projections onto the feasible region, which is the intersection of closed and convex constraints sets, to regain feasibility. The latter poses a computational difficulty, and, therefore, the projected subgradient method is applicable only when the feasible region is “simple to project onto.” In contrast to this, in the superiorization methodology a feasibility-seeking algorithm leads the overall process, and objective function steps are interlaced into it. This makes a difference because the feasibility-seeking algorithm employs projections onto the individual constraints sets and not onto the entire feasible region.

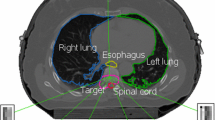
We present the two approaches side-by-side and demonstrate their performance on a problem of computerized tomography image reconstruction, posed as a constrained minimization problem aiming at finding a constraint-compatible solution that has a reduced value of the total variation of the reconstructed image.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

References

  1. Ruszczyński, A.: Nonlinear Optimization. Princeton University Press, Princeton (2006)

    MATH  Google Scholar 

  2. Nesterov, Y.: Introductory Lectures on Convex Optimization. Kluwer Academic, Doredrecht (2004)

    Book  MATH  Google Scholar 

  3. Shor, N.Z.: Minimization Methods for Non-Differentiable Functions. Springer, Berlin (1985)

    Book  MATH  Google Scholar 

  4. Poljak, B.T.: A general method of solving extremum problems. Sov. Math. Dokl. 8, 593–597 (1967)

    Google Scholar 

  5. Polyak, B.T.: Minimization of unsmooth functionals. USSR Comput. Math. Math. Phys. 9, 14–29 (1969)

    Article  Google Scholar 

  6. Beck, A., Teboulle, M.: Mirror descent and nonlinear projected subgradient methods for convex optimization. Oper. Res. Lett. 31, 167–175 (2003)

    Article  MATH  MathSciNet  Google Scholar 

  7. Butnariu, D., Davidi, R., Herman, G.T., Kazantsev, I.G.: Stable convergence behavior under summable perturbations of a class of projection methods for convex feasibility and optimization problems. IEEE J. Sel. Top. Signal Process. 1, 540–547 (2007)

    Article  Google Scholar 

  8. Censor, Y., Elfving, T., Herman, G.T.: Averaging strings of sequential iterations for convex feasibility problems. In: Butnariu, D., Censor, Y., Reich, S. (eds.) Inherently Parallel Algorithms in Feasibility and Optimization and Their Applications, pp. 101–114. Elsevier, Amsterdam (2001)

    Chapter  Google Scholar 

  9. Censor, Y., Segal, A.: On the string averaging method for sparse common fixed point problems. Int. Trans. Oper. Res. 16, 481–494 (2009)

    Article  MATH  MathSciNet  Google Scholar 

  10. Censor, Y., Segal, A.: On string-averaging for sparse problems and on the split common fixed point problem. Contemp. Math. 513, 125–142 (2010)

    Article  MathSciNet  Google Scholar 

  11. Censor, Y., Tom, E.: Convergence of string-averaging projection schemes for inconsistent convex feasibility problems. Optim. Methods Softw. 18, 543–554 (2003)

    Article  MATH  MathSciNet  Google Scholar 

  12. Penfold, S.N., Schulte, R.W., Censor, Y., Bashkirov, V., McAllister, S., Schubert, K.E., Rosenfeld, A.B.: Block-iterative and string-averaging projection algorithms in proton computed tomography image reconstruction. In: Censor, Y., Jiang, M., Wang, G. (eds.) Biomedical Mathematics: Promising Directions in Imaging, Therapy Planning and Inverse Problems, pp. 347–367. Medical Physics, Madison (2010)

    Google Scholar 

  13. Censor, Y., Davidi, R., Herman, G.T.: Perturbation resilience and superiorization of iterative algorithms. Inverse Probl. 26, 065008 (2010)

    Article  MathSciNet  Google Scholar 

  14. Davidi, R., Herman, G.T., Censor, Y.: Perturbation-resilient block-iterative projection methods with application to image reconstruction from projections. Int. Trans. Oper. Res. 16, 505–524 (2009)

    Article  MATH  MathSciNet  Google Scholar 

  15. Herman, G.T., Davidi, R.: Image reconstruction from a small number of projections. Inverse Probl. 24, 045011 (2008)

    Article  MathSciNet  Google Scholar 

  16. Nikazad, T., Davidi, R., Herman, G.: Accelerated perturbation-resilient block-iterative projection methods with application to image reconstruction. Inverse Probl. 28, 035005 (2012)

    Article  MathSciNet  Google Scholar 

  17. Penfold, S.N., Schulte, R.W., Censor, Y., Rosenfeld, A.B.: Total variation superiorization schemes in proton computed tomography image reconstruction. Med. Phys. 37, 5887–5895 (2010)

    Article  Google Scholar 

  18. Aharoni, R., Censor, Y.: Block-iterative projection methods for parallel computation of solutions to convex feasibility problems. Linear Algebra Appl. 120, 165–175 (1989)

    Article  MATH  MathSciNet  Google Scholar 

  19. Bauschke, H.H., Borwein, J.M.: On projection algorithms for solving convex feasibility problems. SIAM Rev. 38, 367–426 (1996)

    Article  MATH  MathSciNet  Google Scholar 

  20. Bauschke, H.H., Combettes, P.L.: Convex Analysis and Monotone Operator Theory in Hilbert Spaces. Springer, New York (2011)

    Book  MATH  Google Scholar 

  21. Censor, Y., Chen, W., Combettes, P.L., Davidi, R., Herman, G.T.: On the effectiveness of projection methods for convex feasibility problems with linear inequality constraints. Comput. Optim. Appl. 51, 1065–1088 (2012)

    Article  MATH  MathSciNet  Google Scholar 

  22. Censor, Y., Zenios, S.A.: Parallel Optimization: Theory, Algorithms, and Applications. Oxford University Press, New York (1997)

    MATH  Google Scholar 

  23. Cegielski, A.: Iterative Methods for Fixed Point Problems in Hilbert Spaces. Lecture Notes in Mathematics, vol. 2057. Springer, Berlin (2012)

    MATH  Google Scholar 

  24. Herman, G.T., Garduño, E., Davidi, R., Censor, Y.: Superiorization: an optimization heuristic for medical physics. Med. Phys. 39, 5532–5546 (2012)

    Article  Google Scholar 

  25. Jin, W., Censor, Y., Jiang, M.: A heuristic superiorization-like approach to bioluminescence tomography. In: International Federation for Medical and Biological Engineering (IFMBE) Proceedings, vol. 39, pp. 1026–1029 (2012)

    Google Scholar 

  26. Luo, S., Zhou, T.: Superiorization of EM algorithm and its application in single-photon emission computed tomography (SPECT). Inverse Problems and Imaging. Accepted for publication

  27. Bauschke, H.H., Koch, V.R.: Projection methods: swiss army knives for solving feasibility and best approximation problems with halfspaces. In: Reich, S., Zaslavski, A. (eds.) Proceedings of the Workshop “Infinite Products of Operators and Their Applications”, Haifa, 2012 (2013). Accepted for publication https://people.ok.ubc.ca/bauschke/Research/c16.pdf

    Google Scholar 

  28. Helou Neto, E.S., De Pierro, Á.R.: Incremental subgradients for constrained convex optimization: a unified framework and new methods. SIAM J. Optim. 20, 1547–1572 (2009)

    Article  MATH  MathSciNet  Google Scholar 

  29. Helou Neto, E.S., De Pierro, Á.R.: On perturbed steepest descent methods with inexact line search for bilevel convex optimization. Optimization 60, 991–1008 (2011)

    Article  MATH  MathSciNet  Google Scholar 

  30. Nedić, A.: Random algorithms for convex minimization problems. Math. Program., Ser. B 129, 225–253 (2011)

    Article  MATH  Google Scholar 

  31. Ram, S.S., Nedić, A., Veeravalli, V.: Incremental stochastic subgradient algorithms for convex optimization. SIAM J. Optim. 20, 691–717 (2009)

    Article  MATH  MathSciNet  Google Scholar 

  32. Nurminski, E.A.: The use of additional diminishing disturbances in Fejer models of iterative algorithms. Comput. Math. Math. Phys. 48, 2154–2161 (2008). Original Russian text: Nurminski, E.A.: Ž. Vyčisl. Mat. Mat. Fiz. 48, 2121–2128 (2008)

    Article  MathSciNet  Google Scholar 

  33. Nurminski, E.A.: Fejer processes with diminishing disturbances. Dokl. Math. 78, 755–758 (2008). Original Russian text: Nurminski, E.A.: Dokl. Akad. Nauk SSSR 422, 601–604 (2008)

    Article  MATH  MathSciNet  Google Scholar 

  34. Nurminski, E.A.: Envelope stepsize control for iterative algorithms based on Fejer processes with attractants. Optim. Methods Softw. 25, 97–108 (2010)

    Article  MATH  MathSciNet  Google Scholar 

  35. Nurminski, E.A.: Fejer algorithms with an adaptive step. Comput. Math. Math. Phys. 51, 741–750 (2011). Original Russian text: Nurminski, E.A.: Ž. Vyčisl. Mat. Mat. Fiz. 51, 791–801 (2011)

    Article  MathSciNet  Google Scholar 

  36. Sidky, E.Y., Kao, C., Pan, X.: Image reconstruction in circular cone-beam computed tomography by constrained, total-variation minimization. Phys. Med. Biol. 53, 4777–4807 (2008)

    Article  Google Scholar 

  37. Herman, G.T.: Fundamentals of Computerized Tomography: Image Reconstruction from Projections, 2nd edn. Springer, Berlin (2009)

    Book  Google Scholar 

  38. Combettes, P.L., Pesquet, J.C.: Image restoration subject to a total variation constraint. IEEE Trans. Image Process. 13, 1213–1222 (2004)

    Article  Google Scholar 

  39. Nesterov, Y.E.: A method for solving the convex programming problem with convergence rate O(1/k 2). Sov. Math. Dokl. 27, 372–376 (1983)

    MATH  Google Scholar 

  40. Güler, O.: Complexity of smooth convex programming and its applications. In: Pardalos, P.M. (ed.) Complexity of Numerical Optimization, pp. 180–202. World Scientific, Singapore (1993)

    Chapter  Google Scholar 

  41. Davidi, R., Herman, G.T., Klukowska, J.: SNARK09: A programming system for the reconstruction of 2D images from 1D projections (2009). http://www.dig.cs.gc.cuny.edu/software/snark09/

  42. Klukowska, J., Davidi, R., Herman, G.T.: SNARK09—A software package for reconstruction of 2D images from 1D projections. Comput. Methods Programs Biomed. 110, 424–440 (2013)

    Article  Google Scholar 

Download references

Acknowledgements

We thank the editor and reviewer for their constructive comments. We would like to acknowledge the generous support by Dr. Ernesto Gomez and Dr. Keith Schubert in allowing us to use the GPU cluster at the Department of Computer Science and Engineering at California State University San Bernardino. We are also grateful to Joanna Klukowska for her advice on using optimized compilation for speeding up SNARK09. This work was supported by the United States–Israel Binational Science Foundation (BSF) Grant No. 200912, the U.S. Department of Defense Prostate Cancer Research Program Award No. W81XWH-12-1-0122, the National Science Foundation Award No. DMS-1114901, the U.S. Department of Army Award No. W81XWH-10-1-0170, and by Grant No. R01EB013118 from the National Institute of Biomedical Imaging and Bioengineering and the National Science Foundation. The contents of this publication is solely the responsibility of the authors and does not necessarily represent the official views of the National Institute of Biomedical Imaging and Bioengineering or the National Institutes of Health.

Author information

Authors and Affiliations

  1. Department of Mathematics, University of Haifa, Mt. Carmel, 3190501, Haifa, Israel

    Yair Censor & Luba Tetruashvili

  2. Department of Radiation Oncology, Stanford University, Stanford, CA, 94305, USA

    Ran Davidi

  3. Department of Computer Science, The Graduate Center, City University of New York, New York, NY, 10016, USA

    Gabor T. Herman

  4. Department of Radiation Medicine, Loma Linda University Medical Center, Loma Linda, CA, 92354, USA

    Reinhard W. Schulte

Authors
  1. Yair Censor
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ran Davidi
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Gabor T. Herman
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Reinhard W. Schulte
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Luba Tetruashvili
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yair Censor.

Additional information

Communicated by Masao Fukushima.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Censor, Y., Davidi, R., Herman, G.T. et al. Projected Subgradient Minimization Versus Superiorization. J Optim Theory Appl 160, 730–747 (2014). https://doi.org/10.1007/s10957-013-0408-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10957-013-0408-3

Keywords

Search

Navigation