The Phase Diagram for a Multispecies Left-Permeable Asymmetric Exclusion Process

Abstract

We study a multispecies generalization of a left-permeable asymmetric exclusion process (LPASEP) in one dimension with open boundaries. We determine all phases in the phase diagram using an exact projection to the LPASEP solved by us in a previous work. In most phases, we observe the phenomenon of dynamical expulsion of one or more species. We explain the density profiles in each phase using interacting shocks. This explanation is corroborated by simulations.

Appendix A: The Even mLPASEP

We explain the salient features of the phase diagram of the even mLPASEP focusing on the aspects that make the analysis more complicated than that for the odd mLPASEP.

The computation of the generalized phase diagram for the even mLPASEP requires us to project to the single-species ASEP [22] which we review briefly. The ASEP involves only particles and vacancies, denoted by 1 and $\overline{1}$ respectively. The boundary transitions, in accord with our definitions in Eq. (5) and (4), have the following rates:

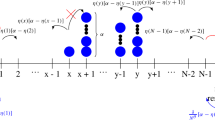
The relevant left and right boundary parameters are $\lambda = \kappa _{\alpha _{1}, \gamma '_{0}}^{+}$ and $b = \kappa _{\beta , \delta }^{+}$ respectively, where $\kappa ^\pm _{u,v}$ is defined in (7). With this notation, the phase diagram formally looks exactly like Fig. 1 with the same nomenclature for the phases: phase $\overline{\mathbb {1}}$ (MC), 0 (LD) and $\mathbb {1}$ (HD). The currents and densities of species 1 for all three phases are also identical to those in Table 1. The density profiles for ASEP can also be understood by appealing to shocks. Since this is reviewed by Blythe and Evans in [2], we only illustrate the shock picture for the coexistence line $b=\lambda >1$ in Fig. 9, where the shock has zero mean velocity. In the LD (resp. HD) phase, the shock has positive (resp. negative) velocity and is pinned to the right (resp. left).

Fig. 9

The shock picture for ASEP on the co-existence line $b=\lambda >1$

Fig. 10

Time-average densities in four species mLPASEP for species $\overline{2}$ (red circles), $\overline{1}$ (magenta diamonds), 0 (green boxes), 1 (blue crosses) and 2 (black triangles) for a phase $\overline{\mathbb {2}}$ ($\lambda _1 \simeq 0.23 ,\lambda _2 \simeq 0.84, b \simeq 0.65$), b phase $\overline{\mathbb {1}}$ ($\lambda _1 \simeq 0.44, \lambda _2 \simeq 2.65, b \simeq 0.75$), c phase 0 ($\lambda _1 \simeq 2.27, \lambda _2 \simeq 6.5, b \simeq 0.92$), d phase $\mathbb {1}$ ($\lambda _1 \simeq 1.17, \lambda _2 \simeq 6.45, b \simeq 3.09$), e phase $\mathbb {2}$ ($\gamma _1 \simeq 0.12 , q=0.41, \beta =0.15,\delta =0.86, \lambda _1 \simeq 1.17, \lambda _2 \simeq 6.45, b \simeq 9.28$), f 0$-\mathbb {1}$ co-existence line ($\lambda _1 = 3, \lambda _2 \simeq 7.18, b = 3$), and g$\mathbb {1}-\mathbb {2}$ co-existence line ($\lambda _1 \simeq 1.34, \lambda _2 = 6, b = 6$). For all simulations, we fix the lattice size to be 1000 (Color figure online)

Fig. 11

The shock picture for the even mLPASEP on the 0$-\mathbb {1}$ co-existence line

The phase diagrams for the even mLPASEP with 2r species and the odd mLPASEP with $(2r+1)$ species have identical structure as depicted in Fig. 3. The main difference between the two is that the 1-colouring projects the even mLPASEP to the ASEP so that the boundary parameters are $\lambda _{1}=\kappa ^{+}_{\theta _{1}, \gamma '_{0}}$ and $b=\kappa ^{+}_{\beta , \delta }$. All other k-colourings continue to project the even mLPASEP to the LPASEP with boundary parameters $\lambda _{k} = \theta _{k}/\phi '_{k}$ and $b= \kappa ^{+}_{\beta , \delta }$., where $\theta _{k} = \sum _{i=k}^{r} \alpha _{i}$ and $\phi '_{i} = \sum _{i=1}^{k-1}\left( \alpha _{i} + \alpha _{\overline{i}} \right)$ were defined in Sect. 2.2.

Taking into account all possible colourings, there are $r+1$ relevant boundary parameters, namely, $\lambda _{1}, \ldots , \lambda _{r}$ and b. Again, the inequalities $\lambda _{1}< \lambda _{2}< \cdots < \lambda _{r}$ are satisfied. Because of these relations among $\lambda _{i}$’s, we arrive at the same phase diagram in Fig. 3 which shows all $2r+1$ phases in the even mLPASEP. In all phases except phase 0, the densities of all species have the same expression in the even mLPASEP as given in Table 2. In phase 0, the densities of 1 and $\overline{1}$ are $(f(\lambda _{1}) - f(\lambda _{2}))$ and $(\overline{f}(\lambda _{1}) - f(\lambda _{2}))$ respectively. We illustrate the density profiles with simulations for the 4-species even mLPASEP in Fig. 10.

The shock picture in the even mLPASEP is identical to that in the odd mLPASEP in all coexistence lines except the 0$-\mathbb {1}$ boundary.

On this coexistence line, 1’s and $\overline{1}$’s form a shock with zero drift as shown in Fig. 11. The shock is pinned to the right (resp. left) boundary in phase 0 (resp. $\mathbb {1}$). In phase $\overline{\mathbb {1}}$, the density of these two species become equal and the height of the shock goes to zero as the system approaches this phase along the 0$-\mathbb {1}$ coexistence line. We have performed simulations showing instantaneous density profiles for the even mLPASEP with four species on the 0$-\mathbb {1}$ boundary and the results exactly match with the theoretical prediction.