Abstract
We consider the dynamical problem of an antiferromagnetic spin system on a two-dimensional square lattice \(\varepsilon \mathbb {Z}^2\) with nearest-neighbour and next-to-nearest neighbour interactions. The key features of the model include the interaction between spatial scale \(\varepsilon \) and time scale \(\tau \), and the incorporation of interfacial boundaries separating regions with microstructures. By employing a discrete-time variational scheme, a limit continuous-time evolution is obtained for a crystal in \(\mathbb {R}^2\) which evolves according to some motion by crystalline curvatures. In the case of anti-phase boundaries between striped patterns, a striking phenomenon is the appearance of some “non-local” curvature dependence velocity law reflecting the creation of some defect structure on the interface at the discrete level.






























Similar content being viewed by others
Notes
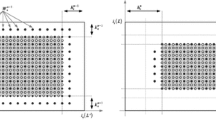
A bisectric direction has slope \(\pm 1\). A bisectric segment is a segment along the bisectric direction.
Note that there is a difference in the definition of the number of layers moving in for the bisectric segments between the \(e_1\)-\(e_2\)-interface in Sect. 4 and the current \(e_1\)-\(-e_1\)-interface. In the former case, the number is measured along the normal bisectric direction while here it is measured along the horizontal direction. This is simply for arithmetic convenience.
References
Alicandro, R., Braides, A., Cicalese, M.: Phase and anti-phase boundaries in binary discrete systems: a variational viewpoint. Netw. Heterog. Media 1, 85–107 (2006)
Allen, S., Cahn, J.: A microscopic theory for antiphase boundary motion and its application to antiphase domain coarsening. Acta Metall. 27, 1084–1095 (1979)
Almgren, F., Taylor, J.E.: Flat flow is motion by crystalline curvature for curves with crystalline energies. J. Differ. Geom. 42, 1–22 (1995)
Almgren, F., Taylor, J.E., Wang, L.: Curvature driven flows: a variational approach. SIAM J. Control Optim. 50, 387–438 (1983)
Ambrosio, L., Gigli, N., Savaré, G.: Gradient Flows in Metric Spaces and in the Space of Probability Measures. Lectures in Mathematics ETH. Zürich. Birkhhäuser, Basel (2008)
Ansini, N., Braides, A., Chiadò Piat, V.: Gradient theory of phase transitions in composite media. Proc. Royal Soc. Edin 133A, 265–296 (2003)
Braides, A.: \(\Gamma \)-convergence for Beginners. Oxford University Press, Oxford (2002)
Braides, A.: Local Minimization, Variational Evolution and Gamma-Convergence. Lecture Notes in Mathematics, vol. 2094. Springer Verlag, Berlin (2014)
Braides, A., Cicalese, M.: Interfaces, modulated phases and textures in lattice systems (to appear in Arch. Ration. Mech. Anal)
Braides, A., Gelli, M.S., Novaga, M.: Motion and pinning of discrete interfaces. Arch. Ration. Mech. Anal. 95, 469–498 (2010)
Braides, A., Scilla, G.: Motion of discrete interfaces in periodic media. Interfaces Free Bound. 15, 451–476 (2013)
Braides, A., Solci, M.: Motion of discrete interfaces through mushy layers. J. Nonlinear Sci. 26, 1031–1053 (2016)
Caffarelli, L.A., de la Llave, R.: Interfaces of ground states in ising models with periodic coefficients. J. Stat. Phys. 118, 687–719 (2005)
Cahn, J.W., Van Vleck, E.S.: Quadrijunctions do not stop two-dimensional grain growth. Scipta Mater. 34, 909–912 (1996)
Cahn, J.W., Van Vleck, E.S.: On the co-existence and stability of trijunctions and quadrijunctions in a simple model. Acta Mater. 47(18), 4627–4639 (1999)
Chen, X.: Generation and propagation of interfaces for reaction-diffusion equations. J. Diff. Equ. 96, 116–141 (1992)
De Masi, A., Ferrai, P.A., Lebowitz, J.L.: Rigorous derivation of reaction-diffusion equations with fluctuations. Phys. Rev. Lett. 55(19), 1947–1949 (1985)
De Masi, A., Ferrai, P.A., Presutti, E.: Reaction-diffusion equations for interacting particle systems. J. Stat. Phys. 44(3/4), 589–644 (1986)
De Masi, A., Orlandi, E., Presutti, E., Triolo, L.: Glauber evolution with the Kac potentials. I. Mesoscopic and macroscopic limits, interface dynamics. Nonlinearity 7(3), 633–696 (1994)
de Mottoni, P., Schatzman, M.: Geometric evolution of developed interfaces. Trans. Am. Math. Soc. 347, 1533–1589 (1995)
Evans, L.C., Soner, H.M., Souganidis, P.E.: Phase transitions and generalized motion by mean curvature. Commun. Pure Appl. Math. 45, 1097–1123 (1992)
Giacomin, G., Lebowitz, J.L.: Phase segregation dynamics in particle systems with long range interactions. I. Macroscopic limits. J. Stat. Phys. 87(1–2), 37–61 (1997)
Giacomin, G., Lebowitz, J.L.: Phase segregation dynamics in particle systems with long range interactions. II. Interface motion. SIAM J. Appl. Math. 58(6), 1707–1729 (1998)
Giuliani, A., Lieb, E.H., Seiringer, R.: Formation of stripes and slabs near the ferromagnetic transition. Commun. Math. Phys. 331, 333–350 (2014)
Giuliani, A., Seiringer, R.: Periodic striped ground states in Ising models with competing interactions. arXiv:1509.00057 (to appear in Comm. Math. Phys)
Glauber, R.J.: Time-dependent statistics of the Ising model. J. Math. Phys. 4(2), 294–307 (1963)
Ilmanen, T.: Convergence of the Allen–Cahn equation to Brakke’s motion by mean curvature. J. Differ. Geom. 38, 417–461 (1993)
Katsoulakis, M.K., Souganidis, P.E.: Interacting particle systems and generalized evolution of fronts. Arch. Ration. Mech. Anal. 127(2), 133–157 (1994)
Katsoulakis, M.K., Souganidis, P.E.: Generalized motion by mean curvature as a macroscopic limit of stochastic Ising models with long range interactions and Glauber dynamics. Commun. Math. Phys. 169(1), 61–97 (1995)
Katsoulakis, M.K., Souganidis, P.E.: Stochastic Ising models and anisotropic front propagation. J. Stat. Phys. 87(1–2), 63–89 (1997)
Kawasaki, K.: Diffusion constant near the critical point for time-dependent ising models. I. Phys. Rev. 145(1), 224–230 (1966)
Kawasaki, K.: Diffusion constant near the critical point for time-dependent ising models. II. Phys. Rev. 148(1), 375–381 (1966)
Kinderlehrer, D., Liu, C.: Evolution of grain boundaries. Math. Models Methods Appl. Sci. 11, 713–729 (2001)
Luckhaus, S., Sturzenhecker, T.: Implicit time discretization for the mean curvature flow. Calc. Var. 3, 253–271 (1995)
Magni, A., Mantegazza, C., Novaga, M.: Motion by curvature of planar networks II. Ann. Sc. Norm. Super. Pisa Cl. Sci. 15, 117–144 (2016)
Mantegazza, C., Novaga, M., Tortorelli, V.M.: Motion by curvature of planar networks. Ann. Sc. Norm. Super. Pisa Cl. Sci. 3, 235–324 (2004)
Modica, L.: The gradient theory of phase transitions and the minimal interface criterion. Arch. Ration. Mech. Anal. 98, 123–142 (1987)
Sandier, E., Serfaty, S.: Gamma-convergence of gradient flows with applications to Ginzburg–Landau. Commun. Pure Appl. Math. 57(12), 1627–1672 (2004)
Sternberg, P.: The effect of a singular perturbation on nonconvex variational problems. Arch. Ration. Mech. Anal. 101, 209–260 (1988)
Taylor, J.E.: Motion of curves by crystalline curvature, including triple junctions and boundary points. Proc. Symp. Pure Math. Differ. Geom. 51(part 1), 417–438 (1993)
Taylor, J.E., Cahn, J., Handwerker, C.: Geometric models of crystal growth. Acta Metall. Mater. 40, 1443–1474 (1992)
Taylor, J.E., Cahn, J., Handwerker, C.: Mean curvature and weighted mean curvature. Acta Metall. Mater. 40, 1475–1485 (1992)
Taylor, J.E.: A variational approach to crystalline triple-junction motion. J. Stat. Phys. 95(5–6), 1221–1244 (1999)
Acknowledgments
The authors would like to thank the hospitality of the Institute for Mathematics and Its Applications (IMA), Minnesota, it was where this project started. The second author was supported by the DFG Collaborative Research Center TRR 109 Discretization in Geometry and Dynamics. The third author also appreciates the hosting by the Dipartimento di Matematica, Università degli Studi di Roma Tor Vergata of his several visits which facilitated the completion of this project.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Braides, A., Cicalese, M. & Yip, N.K. Crystalline Motion of Interfaces Between Patterns. J Stat Phys 165, 274–319 (2016). https://doi.org/10.1007/s10955-016-1609-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10955-016-1609-6