Abstract
Consider a quantum system S weakly interacting with a very large but finite system B called the heat bath, and suppose that the composite S∪B is in a pure state Ψ with participating energies between E and E+δ with small δ. Then, it is known that for most Ψ the reduced density matrix of S is (approximately) equal to the canonical density matrix. That is, the reduced density matrix is universal in the sense that it depends only on S’s Hamiltonian and the temperature but not on B’s Hamiltonian, on the interaction Hamiltonian, or on the details of Ψ. It has also been pointed out that S can also be attributed a random wave function ψ whose probability distribution is universal in the same sense. This distribution is known as the “Scrooge measure” or “Gaussian adjusted projected (GAP) measure”; we regard it as the thermal equilibrium distribution of wave functions. The relevant concept of the wave function of a subsystem is known as the “conditional wave function.” In this paper, we develop analogous considerations for particles with spin. One can either use some kind of conditional wave function or, more naturally, the “conditional density matrix,” which is in general different from the reduced density matrix. We ask what the thermal equilibrium distribution of the conditional density matrix is, and find the answer that for most Ψ the conditional density matrix is (approximately) deterministic, in fact (approximately) equal to the canonical density matrix.
Similar content being viewed by others
Notes
By a GONB we mean that which is provided by a unitary isomorphism
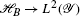 for some measure space
for some measure space 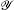 containing the y; this includes the possibility of a continuous basis such as the position basis.
containing the y; this includes the possibility of a continuous basis such as the position basis.This factor, \(\mathcal{N}=\|\varPsi(\cdot ,Y)\|\), will fail to be well defined if Ψ(⋅,Y) fails to be square-integrable. However, the Y for which this happens form a set of measure zero because ∫dy ∥Ψ(⋅,y)∥2=∫dy∫dx |Ψ(x,y)|2<∞. The factor \(\mathcal{N}\) could be zero, but since Y has distribution density ∥Ψ(⋅,y)∥2, also this case occurs with probability zero.
If
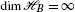 , we can also admit a GONB. Since we assume here that
, we can also admit a GONB. Since we assume here that 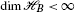 , every GONB is an ONB.
, every GONB is an ONB.The point here is that we can change the order of the quantifiers (“for most y” etc.) without changing the content of the statement; this was not possible as long as the notion of “most y” depended on Ψ.
Actually, we use here more than just large
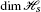 ; we use that among the eigenvalues of \(\rho_{\beta}^{S}\otimes\rho_{\beta}^{s}\) are not just a few dominating ones while all others are negligible, but that many of them are of comparable size; that is the case since H
s
has a reasonable distribution of eigenvalues.
; we use that among the eigenvalues of \(\rho_{\beta}^{S}\otimes\rho_{\beta}^{s}\) are not just a few dominating ones while all others are negligible, but that many of them are of comparable size; that is the case since H
s
has a reasonable distribution of eigenvalues.
References
Billingsley, P.: Probability and Measure, 3rd edn. Wiley, New York (1995)
Dürr, D., Goldstein, S., Tumulka, R., Zanghì, N.: On the role of density matrices in Bohmian mechanics. Found. Phys. 35, 449–467 (2005). http://arxiv.org/abs/quant-ph/0311127
Dürr, D., Goldstein, S., Zanghì, N.: Quantum equilibrium and the origin of absolute uncertainty. J. Stat. Phys. 67, 843–907 (1992). http://arxiv.org/abs/quant-ph/0308039
Gaspard, P., Nagaoka, M.: Non-Markovian stochastic Schrödinger equation. J. Chem. Phys. 111(13), 5676–5690 (1999)
Gemmer, J., Mahler, G., Michel, M.: Quantum Thermodynamics: Emergence of Thermodynamic Behavior within Composite Quantum Systems. Springer, Berlin (2004)
Goldstein, S., Lebowitz, J.L., Mastrodonato, C., Tumulka, R., Zanghì, N.: Universal probability distribution for the wave function of an open quantum system. Preprint http://arxiv.org/abs/1104.5482 (2011)
Goldstein, S., Lebowitz, J.L., Tumulka, R., Zanghì, N.: Canonical typicality. Phys. Rev. Lett. 96, 050403 (2006). http://arxiv.org/abs/cond-mat/0511091
Goldstein, S., Lebowitz, J.L., Tumulka, R., Zanghì, N.: On the distribution of the wave function for systems in thermal equilibrium. J. Stat. Phys. 125, 1193–1221 (2006). http://arxiv.org/abs/quant-ph/0309021
Jozsa, R., Robb, D., Wootters, W.K.: Lower bound for accessible information in quantum mechanics. Phys. Rev. A 49, 668–677 (1994)
Popescu, S., Short, A.J., Winter, A.: The foundations of statistical mechanics from entanglement. Preprint http://arxiv.org/abs/quant-ph/0511225 (2005)
Popescu, S., Short, A.J., Winter, A.: Entanglement and the foundation of statistical mechanics. Nat. Phys. 21(11), 754–758 (2006)
Reimann, P.: Typicality of pure states randomly sampled according to the Gaussian adjusted projected measure. J. Stat. Phys. 132(5), 921–935 (2008). http://arxiv.org/abs/0805.3102
Tolman, R.C.: The Principles of Statistical Mechanics. Oxford University Press, London (1938)
Tumulka, R., Zanghì, N.: Smoothness of wave functions in thermal equilibrium. J. Math. Phys. 46, 112104 (2005). http://arxiv.org/abs/math-ph/0509028
Acknowledgements
R.T. was supported by grant no. 37433 from the John Templeton Foundation.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Pandya, V., Tumulka, R. Spin and the Thermal Equilibrium Distribution of Wave Functions. J Stat Phys 154, 491–502 (2014). https://doi.org/10.1007/s10955-013-0849-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10955-013-0849-y




 for some measure space
for some measure space 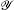 containing the y; this includes the possibility of a continuous basis such as the position basis.
containing the y; this includes the possibility of a continuous basis such as the position basis.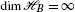 , we can also admit a GONB. Since we assume here that
, we can also admit a GONB. Since we assume here that 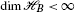 , every GONB is an ONB.
, every GONB is an ONB.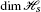 ; we use that among the eigenvalues of
; we use that among the eigenvalues of