Phase Equilibria of Ternary Liquid–Liquid Systems (Water + C1–C4 Monocarboxylic Acids + Dibutyl Ether) at Three Different Temperatures: Modeling with A-UNIFAC

Abstract

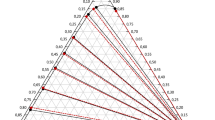
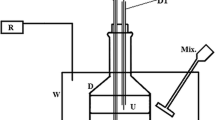
Liquid–liquid equilibrium (LLE) data for the ternary systems composed of water, C1–C4 monocarboxylic acids, and dibutyl ether were determined at three different temperatures (293.15, 303.15, and 313.15 K) and atmospheric pressure. The experimental solubility curves and mutual solubilities of (water + dibutyl ether) were determined by the cloud-point method, whereas the tie-lines of conjugate phases were obtained via GC analysis. The examined C1–C4 monocarboxylic acids are valuable components for estimating the effect of acid structure on LLE. The separation factor calculated from experimental LLE data is indicative of the ability of the solvent to effectively recover the acid. Equilibrium distribution of C1–C4 acids is better for more structured propionic and butyric acids as compared to less structured formic and acetic acids, and the general ranking with respect to the separation factor (S) follows the order: C4 > C3 > C2 > C1, and T_293.15 < T_303.15 ≤ T_313.15. The LLE data were predicted with the group-contribution method A-UNIFAC with the newly estimated parameters, which shows an appropriate consistency with the experimental data.

Appendix: A-UNIFAC

Mengarelli et al. [35] modified the original UNIFAC model presented by Fredenslund et al. [55] to take into account the associative effects in the calculation of activity coefficients. This model called A-UNIFAC adds an associative (assoc) term based on Wertheim's theory [39] to the original combinatorial (comb) and residual (res) expressions [40], and applies an approach to group contributions [56].

The non-ideal behavior is described as the sum of three independent contributions to the excess Gibbs energy function:

$$G^{{\text{E}}} \, = \,G^{{{\text{comb}}}} \, + \,G^{{{\text{res}}}} \, + \,G^{{{\text{asso}}c}}$$

(2)

which in terms of the activity coefficient of a compound i in a multicomponent solution is:

$$\gamma \, = \,\gamma ^{{{\text{comb}}}} \gamma ^{{{\text{res}}}} \gamma ^{{{\text{assoc}}}}$$

(3)

The combinatorial and residual contributions are the same as in the UNIFAC model [55]. The associative contribution to the activity coefficient γ_assoc is derived from the association residual Helmholtz energy [57,58,59], which is function of the fraction of non-bonded sites in the solution, $X^{{A_{k} }}$ and in pure component i, $X_{i}^{{A_{k} }}$. It can be written as:

$$\ln \gamma_{i}^\text{assoc} = \sum\limits_{k = 1}^{NGA} {\left\{ {\nu_{k}^{i} \sum\limits_{{A_{k} }}^{{}} {\left[ {\ln \left( {\frac{{X^{{A_{k} }} }}{{X_{i}^{{A_{k} }} }}} \right) + \frac{{X_{i}^{{A_{k} }} - X^{{A_{k} }} }}{2}} \right]} + \sum\limits_{{A_{k} }}^{{}} {\left( {\frac{1}{{X^{{A_{k} }} }} - \frac{1}{2}} \right)N_{k} \left( {\frac{{\partial X^{{A_{k} }} }}{{\partial n_{i} }}} \right)_{{T,P,n_{j} }} } } \right\}}$$

(4)

where N_k is the number of moles of associating group k, $\nu_{k}^{i}$ is the number of associative groups of type k present in the compound i and the last term is the partial derivative of $X^{{A_{k} }}$ with regards to the number of moles n_i of this compound. The summation is extended to all NGA associating groups and A_k associating sites.

The fraction of non-bonded sites, $X^{{A_{k} }}$ and the fraction non-bonded sites in the pure component i, $X_{i}^{{A_{k} }}$ are functions of the associating group density in the mixture $\rho_{j}$ and in the pure component i $(\rho_{j} )_{i}$, respectively, together with the association strength $\mathop \Delta \nolimits^{{A_{k} B_{j} }}$ between site A of group k and site B of group j. These expressions, respectively, are:

$$X^{{A_{k} }} = \left[ {1 + \sum\limits_{j = 1}^{NGA} {\sum\limits_{{B_{j} }}^{{}} {\rho_{j}^{{}} X^{{B_{j} }} \Delta^{{A_{k} B_{j} }} } } } \right]^{ - 1}$$

(5)

$$X_{i}^{{A_{k} }} = \left[ {1 + \sum\limits_{j = 1}^{NGA} {\sum\limits_{{B_{j} }}^{{}} {(\rho_{j} )_{i} X_{i}^{{B_{j} }} \Delta^{{A_{k} B_{j} }} } } } \right]^{ - 1}$$

(6)

where the sum is extended to all the NGA associative groups and B_j active sites of each group.

The density of the associative group j in the mixture $\rho_{j}$ and in the pure component i $(\rho_{j} )_{i}$ are dimensionless and are calculated through the standardized Van der Waals volumes r_i of each component of the mixture:

$$\rho _{j} = {{\sum\limits_{{i = 1}}^{{NC}} {\nu _{j}^{i} x_{i} } } \mathord{\left/ {\vphantom {{\sum\limits_{{i = 1}}^{{NC}} {\nu _{j}^{i} x_{i} } } {\sum\limits_{{i = 1}}^{{NC}} {r_{i} x_{i} } }}} \right. \kern-\nulldelimiterspace} {\sum\limits_{{i = 1}}^{{NC}} {r_{i} x_{i} } }}$$

(7)

and

$$(\rho_{j} )_{i} = {{\nu_{j}^{i} } \mathord{\left/ {\vphantom {{\nu_{j}^{i} } {r_{i} }}} \right. \kern-\nulldelimiterspace} {r_{i} }}$$

(8)

where NC is the total number of components of the mixture, $\nu_{j}^{i}$ is the number of times that the associative group j is present in the molecule i and x_i represents the molar fractions of the component i in the mixture.

The association strength $\mathop \Delta \nolimits^{{A_{k} B_{j} }}$ is a function of the temperature and the energy $\mathop \varepsilon \nolimits^{{A_{k} B_{j} }}$(K) and volume $\mathop \kappa \nolimits^{{A_{k} B_{j} }}$ (cm³·mol^–1) of association, respectively, are represented by a model of association potential of the square-well type:

$$\mathop \Delta \nolimits^{{A_{k} B_{j} }} = \mathop \kappa \nolimits^{{A_{k} B_{j} }} \left[ {\exp \left( {\mathop \varepsilon \nolimits^{{A_{k} B_{j} }} /kT} \right) - 1} \right]$$

(9)

The evaluation of $\gamma_{i}^{{{\text{assoc}}}}$ in Eq. 3 requires the calculation of partial derivatives of the fraction of non-bonded groups. However, Michelsen and Hendriks [60] applied a minimization procedure that simplifies calculations by avoiding such derivatives. Appling this approach, then Eq. 3 is reduced to:

$$\text{ln}\gamma_{i}^{{{\text{assoc}}}} = \sum\limits_{k = 1}^{NGA} {\left\{ {\nu_{k}^{i} \sum\limits_{{A{}_{k}}}^{{}} {\left[ {\text{ln}\left( {\frac{{X^{{A_{k} }} }}{{X_{i}^{{A_{k} }} }}} \right) + \frac{{X_{i}^{{A_{k} }} - 1}}{2}} \right]} + r_{i} \rho_{k} \sum\limits_{{A_{k} }}^{{}} {\left( {\frac{{1 - X^{{A_{k} }} }}{2}} \right)} } \right\}}$$

(10)

The final expression of $\gamma_{i}^{{{\text{assoc}}}}$ in a conventional procedure depends on the amount and type of association sites and species present in the solution with a computation of problem-dependent association effects. However, with the generalized procedure proposed by Tan et al. [61] it is possible to calculate the fraction of non-bonded molecules applicable to all associating systems, regardless of the number and type of associating sites and the number of components in the mixture.