Limiting Partial Molar Volumes (V ^∞₂₃ ) in Solvent (1) − [Solute (2) + Solute (3)] Systems and the Effects of Ionic Hydration on V ^∞₂₃

Abstract

Ionic hydration and electrostriction are very important phenomena in various fields such as medical science, biochemistry, and chemical engineering. The present study is the first to focus on these parameters at infinite dilution. Limiting partial molar volumes (V ^∞₂₃ ) in a solvent (1) − [solute (2) + solute (3)] system were measured at several solute compositions x₃ [= n₃/(n₂ + n₃)] at 30.00 ± 0.05 °C. When the mixed solutes (2 and 3) only slightly ionized, V ^∞₂₃ were observed on the additivity line. This result was attributed to the fact that only solvent (1) molecules can exist around an isolated solute (2) molecule or an isolated solute (3) molecule at infinite dilution. However, V ^∞₂₃ in water − [pyridine + fatty acid (acetic acid, propionic acid, or butyric acid)] systems negatively deviate from the additivity line. By measuring electrical conductivity (κ) and mixing enthalpy (ΔH_mix), the negative deviations of V ^∞₂₃ from the additivity line were attributed to the ionic hydration of pyridine and the fatty acid. As a result, by measuring V ^∞₂₃ at several solute compositions, the electrostriction in water − [pyridine + fatty acid] systems was observed. Conversely, V ^∞₃ in all 14 [solvent (1) + solvent (2)] − solute (3) systems deviated in complicated ways from the additivity line. Unfortunately, we could not clarify the reason behind this deviation because numerous factors had to be considered. Thus, it was confirmed that the behavior of $V_{3}^{\infty }$ is much more complicated than that of V ^∞₂₃ . The solvents used to study V ^∞₂₃ and $V_{3}^{\infty }$ are as follows: water, pyridine, acetic acid, propionic acid, butyric acid, benzene, acetone, chloroform, methanol, ethanol, DMF, carbon tetrachloride, isobutylamine, isobutyl alcohol, n-heptane, and n-octane.

1 Introduction

Recently, we experimentally studied the effects of the vol% of voids (i.e., empty spaces) in a solvent and the repulsive solute–solvent interactions, on limiting partial molar volumes ($V_{2}^{\infty }$) in solvent (1) − solute (2) systems at infinite dilution [1]. In the present paper, we experimentally studied the behavior of V ^∞₂₃ in solvent (1) − [solute (2) + solute (3)] systems at an infinite dilution. Furthermore, for comparison, the behavior of $V_{3}^{\infty }$ in [solvent (1) + solvent (2)] − solute (3) systems has been investigated.

Generally, $V_{2}^{\infty }$ in solvent (1) − solute (2) systems is defined by Eq. 1 at an infinite dilution.

$$ V_{2}^{\infty } \equiv \left( {\frac{\partial V}{{\partial n_{2} }}} \right)_{{T,P,n_{1} }} $$

(1)

where V is the volume of the system, n₁ and n₂ denote the numbers of moles of solvent (1) and solute (2), respectively, and T and P denote the temperature (K) and pressure (Pa), respectively. In Eq. 1, $V_{2}^{\infty }$ is the limiting value when n₂ approaches zero. That is, $V_{2}^{\infty } \equiv \mathop {\lim }\limits_{{n_{2} \to 0}} V_{2}.$ Therefore, $V_{2}^{\infty }$ corresponds to the volume increment of the system when 1 mol of solute (2) is dissolved in a large amount of solvent (1) under constant temperature and pressure.

V ^∞₂₃ in solvent (1) − [solute (2) + solute (3)] systems can be expressed by Eq. 2 at infinite dilution.

$$ V_{23}^{\infty } \equiv \left( {\frac{\partial V}{{\partial n_{23} }}} \right)_{{T,P, n_{1} }} $$

(2)

where V is the volume of the system, n₁ and n₂₃ are the mole number of solvent (1) and the mixed solutes (2 and 3), respectively. $V_{23}^{\infty }$ corresponds to the volume increment of the system when 1 mol of the mixed solutes (2 and 3) is dissolved in a large amount of solvent (1) under constant temperature and pressure. In Eq. 2, $V_{23}^{\infty }$ is the limit value when n₂₃ approaches zero. That is, $V_{23}^{\infty } \equiv \mathop {\lim }\limits_{{n_{23} \to 0}} V_{23}.$Therefore, $V_{23}^{\infty }$ at infinite dilution will reflect the volume occupied by a single hypothetical mixed molecule with average properties. Thus, it can be considered that $V_{23}^{\infty }$ reflects the volume occupied by one isolated solute (2) molecule or by one isolated solute (3) molecule at an infinite dilution.

In this study, $V_{23}^{\infty }$ in each solvent (1) − [solute (2) + solute (3)] system were measured at several solute compositions (x₃) at 30.00 ± 0.05 °C. Here x₃ can be expressed as follows:

$$ x_{3} = \frac{{n_{3} }}{{n_{2} + n_{3} }} $$

(3)

where n₂ and n₃ are mole numbers of solute (2) and solute (3), respectively.

When the mixed solutes (2 and 3) are slightly ionized, $V_{23}^{\infty }$ values were observed on the additivity line. However, $V_{23}^{\infty }$ in water − [pyridine + fatty acid] systems deviated negatively from the additivity line. As pyridine and fatty acids are a weak organic base and a weak organic acid, respectively, they are expected to ionize according to the acid–base chemistry in water at an infinite dilution. Therefore, the reason for the negative deviation of $V_{23}^{\infty }$ from the additivity line was investigated by measuring the electrical conductivity (κ) and mixing enthalpy (ΔH_mix).

For comparison, $V_{3}^{\infty }$ in each [solvent (1) + solvent (2)] − solute (3) system was measured at several solvent compositions (x₂) at 30.00 ± 0.05 °C. Here, V ^∞₃ and x₂ can be expressed by Eqs. 4 and 5, respectively.

$$ V_{3}^{\infty } = \left( {\frac{\partial V}{{\partial n_{3} }}} \right)_{{T,P,n_{12} }} $$

(4)

$$ {x_{2}} = \frac{n_{2}}{n_{1} + n_{2}}.$$

(5)

2 Experimental

2.1 Chemicals

Organic solvents of JIS special grade (purity: ≥ 99%) purchased from Kanto Chemical Co., Inc. and ion-exchanged water purchased from Kishida Chemical Co., Ltd. were used without further purification. Experimental samples were prepared by weight.

2.2 Calculation of V ^∞₂₃

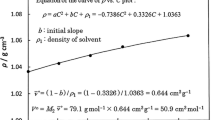
V ^∞₂₃ /cm³·mol⁻¹ values were calculated using an equation of the approximation curve of ρ vs. C plot, where ρ/g·cm⁻³ is the density of the solution and C/g·cm⁻³ is the mass concentration of the solute. Here, the approximation curve of ρ vs. C plot was calculated by the least-squares method. The instrument used for density measurements was a Lipkin–Davison type pycnometer with a capacity of 5 cm³. The volume scale of the pycnometer was calibrated using degassed ion-exchanged water with an apparent density of 0.99449 g·cm⁻³, i.e., 0.99565 g·cm⁻³ subtracted by air density 0.00116 g·cm⁻³. $V_{23}^{\infty }$ in each solvent (1) − [solute (2) + solute (3)] system was determined at several x₃ at 30.00 ± 0.05 °C.

Detailed methods for measuring ρ and calculating $V_{23}^{\infty }$ are presented in previous research [1]. For example, the extrapolation procedure and the graph (ρ vs. C plot) for calculating $V_{2}^{\infty }$ in the acetic acid (1) − pyridine (2) system are given in Fig. 1 of the previous paper [1]. In this graph, $V_{2}^{\infty }$ in the acetic acid (1) − pyridine (2) system is given as 50.9 cm³·mol⁻¹.

Fig. 1

Dependence of $V_{23}^{\infty }$ in solvent (1) − [solute (2) + solute (3)] systems, where the mixed solutes (2 and 3) only slightly ionized, on x₃ at 30.00 ± 0.05 °C. Here, x₃ is the solute composition expressed by the following equation: x₃ = n₃/(n₂ + n₃), where n₂ and n₃ are mole numbers of solute (2) and solute (3), respectively

The measurement precision of $V_{23}^{\infty }$ was estimated to be within 1% by referring to both the $V_{2}^{\infty }$ values reported by several other researchers [2] and the reproducibility of $V_{2}^{\infty }$ of water in 23 different solvents where $V_{2}^{\infty }$ of water in the respective solvent was measured twice by us [1].

2.3 Measurement of Electrical Conductivity (κ)

κ/mS·cm⁻¹ values of a solution comprising solvent (1) (95 wt%) and [solute (2) + solute (3)] (5 wt%) were measured at several x₃ at 30 °C using a conductivity meter (ECTestr 11) purchased from the AS ONE Corporation. The operation of this instrument was extremely simple because the κ values are directly shown. The κ data can be considered to be approximately the values at infinite dilution because of the small value of 5 wt% of [solute (2) + solute (3)]. The precision of the used conductivity meter was 1 μS·cm⁻¹.

2.4 Measurement of Mixing Enthalpy (ΔH _mix)

Mixing enthalpy (ΔH_mix)/kJ·mol⁻¹ values were measured by mixing 5 g of [solute (2) + solute (3)] into 95 g of solvent (1) at several x₃ at 27 °C. Here, ΔH_mix corresponds to the dissolution enthalpy of the mixed solutes (2 and 3), when 1 mol of them is dissolved into a large amount of solvent (1). The detailed method for measuring ΔH_mix is presented in a previous study [1]. A schematic of the apparatus used for measuring ΔH_mix is shown in Fig. 2 of our previous paper [1]. As shown in this figure, all ΔH_mix were measured in a measurement room with temperature of 27 °C. Thus, the measurement temperature of H_mix was unfortunately different from those of V ^∞₂₃ , V ^∞₃ and κ. The measurement precision of ΔH_mix was estimated to be ± 5% by referring to both the ΔH_mix values reported by several other researchers [3] and the reproducibility of the ΔH_mix values obtained by us [1].

Fig. 2

Dependence of $V_{23}^{\infty }$ in water − [pyridine + fatty acid] systems on x₃ at 30.00 ± 0.05 °C

3 Results and Discussion

The numerical results of $V_{23}^{\infty }$/cm³·mol⁻¹, $- \Delta V_{23}^{\infty }$/cm³·mol⁻¹, κ/mS·cm⁻¹, ΔH_mix/kJ·mol⁻¹, and $V_{3}^{\infty }$/cm³·mol⁻¹ are presented in Tables 1, 2, 3, 4, and 5, respectively.

Table 1 Numerical results of $V_{23}^{\infty }$ in solvent (1) − [solute (2) + solute (3)] systems at several x₃ [= n₃/(n₂ + n₃)] at 30.00 ± 0.05 °C (refer to Figs. 1 and 2)

Table 2 Numerical results of $- \Delta V_{23}^{\infty }$ in water (1) − [pyridine (2) + fatty acid (3)] systems at several x₃ at 30.00 ± 0.05 °C (refer to Fig. 3)

Table 3 Numerical results of κ of a solution comprising of water (1) (95 wt%) and [pyridine (2) + fatty acid (3)] (5 wt%), at several x₃ at 30 °C (refer to Fig. 4)

Table 4 Numerical results of ΔH_mix measured by mixing 5 g of [solute (2) + solute (3)] into 95 g of solvent (1) at several x₃ at 27 °C (refer to Figs. 5 and 6)

Table 5 Numerical results of $V_{3}^{\infty }$ in [solvent (1) + [solvent (2)] − solute (3) systems at several x₂ [= n₂/(n₁ + n₂)] at 30.00 ± 0.05 °C (refer to Figs. 7 (a), (b), and (c))

3.1 Dependence of $V_{23}^{\infty }$ on x ₃

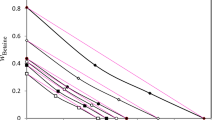
Figure 1 shows the variation of $V_{23}^{\infty }$ in solvent (1) − [solute (2) + solute (3)] systems, where the mixed solutes (2 and 3) can hardly ionize, on x₃ at 30.00 ± 0.05 °C. Here, by measuring κ, we were able to determine that the mixed solutes (2 and 3) were only slightly ionized. All $V_{23}^{\infty }$ values in Fig. 1 were observed on the additivity line, which means the line connecting the point of $V_{23}^{\infty }$ value at x₃ = 0 and the point of $V_{23}^{\infty }$ value at x₃ = 1. These experimental results can be explained as follows. Only solvent (1) molecules can exist around an isolated solute (2) molecule or an isolated solute (3) molecule at infinite dilution. In theory, even if x₃ is changed, the volume occupied by one isolated solute (2) molecule or one isolated solute (3) molecule at infinite dilution should not change. As a result, all $V_{23}^{\infty }$ in Fig. 1 were observed on the additivity line.

However, as shown in Fig. 2, $V_{23}^{\infty }$ in water − [pyridine + fatty acid (acetic acid, propionic acid, or butyric acid)] systems deviated negatively from the additivity line. By measuring the κ and ΔH_mix values, we attempted to clarify the reason why $V_{23}^{\infty }$ deviated from the additivity line.

3.2 Dependences of $- \Delta V_{23}^{\infty }$ and κ on x ₃ (in the Case of Water − [Pyridine + Fatty Acid] Systems)

Figures 3 and 4 show the dependence of $- \Delta V_{23}^{\infty }$ and κ on x₃, respectively, in the case of water − [pyridine + fatty acid] systems. Here, $- \Delta V_{23}^{\infty }$/cm³·mol⁻¹ is the magnitude of the negative deviation of $V_{23}^{\infty }$ from the additivity line. The κ values are considered to be almost proportional to the number of ions. It was found from Figs. 3 and 4 that the shape of the approximation curve of $- \Delta V_{23}^{\infty }$ was substantially similar to the curve of κ. All approximation curves of $- \Delta V_{23}^{\infty }$ and κ had a maximum at x₃ ≈ 0.5. The $- \Delta V_{23}^{\infty }$ values at x₃ = 0 and 1 were naturally zero. The κ values at x₃ = 0 and 1 were nearly zero and very small, respectively.

Fig. 3

Dependence of $- \Delta V_{23}^{\infty }$ on x₃ at 30.00 ± 0.05 °C in the case of water − [pyridine + fatty acid] systems. Here, $- \Delta V_{23}^{\infty }$ is the magnitude of the negative deviation of $V_{23}^{\infty }$ from the additivity line

Fig. 4

Dependence of κ on x₃ at 30 °C in the case of water − [pyridine + fatty acid] systems

From the above experimental results, certain conclusions were drawn. At x₃ = 0.5, all pyridine and fatty acid molecules easily ionize in water, but at x₃ ≠ 0.5, the excess pyridine or fatty acid molecules are only slightly ionized. Therefore, $- \Delta V_{23}^{\infty }$ was proportional to the number of ions of pyridine and the fatty acid. Furthermore, $- \Delta V_{23}^{\infty }$ caused by one pyridine ion is nearly equal to that caused by one fatty acid ion. Therefore, it was concluded from the results of $- \Delta V_{23}^{\infty }$ and κ that negative deviations of $V_{23}^{\infty }$ from the additivity line resulted from the ionization of pyridine and the fatty acid.

The $- \Delta V_{23}^{\infty }$:$V_{23}^{\infty }$ ratio at x₃ = 0.5, calculated from Figs. 2 and 3, is 8.6% (for acetic acid), 8.6% (for propionic acid), and 7.0% (for butyric acid). These large values indicate that the negative deviations of $V_{23}^{\infty }$ from the additivity line are considerable. Here, the relatively small value of 7.0% (butyric acid) may be due to the smallest κ value and the largest van der Waals volume of butyric acid.

3.3 Dependence of ΔH _mix on x ₃

As shown in Fig. 5, ΔH_mix were observed on the additivity line in water − [solute (2) + solute (3)] systems, where the mixed solutes (2 and 3) only slightly ionized. However, as shown in Fig. 6, ΔH_mix deviated negatively from the additivity line in water − [pyridine + fatty acid] systems. Here, ΔH_mix corresponds to the dissolution enthalpy of the mixed solutes (2 and 3), namely pyridine and the fatty acid, when 1 mol of the mixed solutes (2 and 3) was dissolved into a large amount of water, as mentioned in Sect. 2.

Fig. 5

Dependence of ΔH_mix on x₃ at 27 °C in the case of water − [solute (2) + solute (3)] systems, where the mixed solutes (2 and 3) could hardly ionize

Fig. 6

Dependence of ΔH_mix on x₃ at 27 °C in the case of water − [pyridine + fatty acid] systems

Generally, as ΔH_mix decreases, the attractive interaction between solute and solvent molecules increases [1]. Therefore, the above experimental results indicate that $V_{23}^{\infty }$ negatively deviated from the additivity line because of the strong attractive ion–H₂O interaction (i.e., ionic hydration). Generally, ionic hydration breaks the water structure and therefore decreases the distance between the ion and H₂O molecule [4,5,6,7,8,9]. Hence, it can be concluded that ionic hydration largely decreased the volume of the aqueous solution.

From the measurement results of κ and ΔH_mix, it was concluded that the negative deviation of $V_{23}^{\infty }$ from the additivity line resulted from the ionic hydration of pyridine and the fatty acid. Therefore, by measuring $V_{23}^{\infty }$ at several x₃ values, we can observe electrostriction [4,5,6,7,8,9] in water − [pyridine + fatty acid] systems. Here, electrostriction is generally a phenomenon where the volume of a solid or liquid in an electric field (E) decreases in proportion to E².

3.4 Behavior of $V_{3}^{\infty }$ in [Solvent (1) + Solvent (2)] − Solute (3) Systems

For comparison, the behavior of $V_{3}^{\infty }$ in [solvent (1) + solvent (2)] − solute (3) systems was evaluated using a method similar to that used herein. In this case, however, $V_{3}^{\infty }$ in each ternary system was measured at several solvent compositions (x₂ = n₂/(n₁ + n₂)). The 14 systems examined include: [methanol + DMF]–carbon tetrachloride, [isobutylamine + isobutyl alcohol]–water, [water + acetone]–methanol, [methanol + acetone] − benzene, [water + pyridine] − methanol, [chloroform + n-heptane] − acetone, [water + pyridine] − acetic acid, [acetone + n-octane]–benzene, [benzene + n-heptane]–acetone, and [ethanol + chloroform]–benzene, among others.

$V_{3}^{\infty }$ in all 14 systems deviate in a complex manner from the additivity line. For example, the behaviors of $V_{3}^{\infty }$ in [methanol + DMF]–carbon tetrachloride, [isobutylamine + isobutyl alcohol]–water, and [water + acetone]–methanol systems are shown in Fig. 7a, b, and c, respectively. However, we could not clarify the reasons why $V_{3}^{\infty }$ deviated in these ways from the additivity line because the following factors had to be considered: (a) the preferential solvation of solute (3); (b) the coordination number of the solute (3) molecule; (c) the packing density of the mixed solvent (1 and 2) molecules around the solute (3) molecule; and (d) the voids (i.e., empty spaces) in the mixed solvents (1 and 2). Therefore, it was confirmed that the variation of $V_{3}^{\infty }$ is much more complicated than that of $V_{23}^{\infty } .$

Fig. 7

Dependence of $V_{3}^{\infty }$ in [solvent (1) + solvent (2)] − solute (3) systems on x₂ at 30.00 ± 0.05 °C. Here, x₂ is the solvent composition expressed by the following equation: x₂ = n₂/(n₁ + n₂), where n₁ and n₂ are mole numbers of solvent (1) and solvent (2), respectively

4 Conclusion

Ionic hydration and electrostriction are very important phenomena in fields including medical science, biochemistry and chemical engineering. The present research about $V_{23}^{\infty }$ focused on these parameters at infinite dilution. Thus, we were able to obtain clear information about these parameters at infinite dilution, as described below.

The $V_{23}^{\infty }$ values in solvent (1) − [solute (2) + solute (3)] systems, where the mixed solutes (2 and 3) only slightly ionized, were observed on the additivity line. This result indicated that only solvent (1) molecules can exist around an isolated solute (2) molecule or an isolated solute (3) molecule at infinite dilution. Therefore, even if x₃ is changed at infinite dilution, the volume occupied by one isolated solute (2) molecule or one isolated solute (3) molecule must not change. Consequently, all $V_{23}^{\infty }$ values were observed on the additivity line.

However, $V_{23}^{\infty }$ in water − [pyridine + fatty acid (acetic acid, propionic acid, or butyric acid)] systems negatively deviate from the additivity line. From the measurement results of κ and ΔH_mix, the negative deviations of $V_{23}^{\infty }$ from the additivity line were attributed to the ionic hydration of pyridine and the fatty acid. Therefore, by measuring $V_{23}^{\infty }$ at several x₃ values, we can observe electrostriction in water − [pyridine + fatty acid] systems.

Conversely, $V_{3}^{\infty }$ in all 14 [solvent (1) + solvent (2)] − solute (3) systems deviated in complex ways from the additivity line. However, we could not clarify the reasons for this because numerous factors had to be considered. Thus, it was confirmed that the behavior of $V_{3}^{\infty }$ is much more complicated than that of $V_{23}^{\infty }.$ We intend to consider the behavior of $V_{3}^{\infty }$ in each [solvent (1) + solvent (2)] − solute (3) system in more detail by experiment and theory in the future.