Skip to main content
SpringerLink
Log in

A Study on Magnetic Force Characteristics Between Two Cuboidal Permanent Magnets

  • Original Paper
  • Published:
Journal of Superconductivity and Novel Magnetism Aims and scope Submit manuscript

Abstract

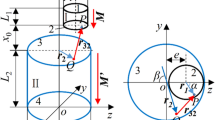
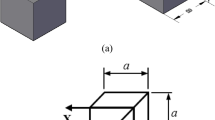
Cuboidal permanent magnets (PMs) are commonly used as elementary magnets for most magnetic systems that work by superposition of magnetic forces. This paper proposed a new method that combines the analytical model with the numerical calculation method to calculate the magnetic forces between two cuboidal PMs with parallel and perpendicular magnetization directions. The assumption was that the magnets were ideal with constant and homogeneous magnetizations. The method was also valid for other magnetization directions and any reference points in space, only needed to rotate the coordinate system and give corresponding distance expressions. An important result was that this method had the advantages of high accuracy and low computational cost, enabling rapid studies of the magnetic force characteristics related to magnet positions, geometric dimensions, and magnetic properties, which were easy to calculate by mathematical software, requiring very little running time. Meanwhile, the calculation results have been validated by comparison with the finite element simulation and experimental measurement. The effects of relative positions, dimensions, and magnetic properties on magnetic force characteristics between the two cuboidal PMs have been studied and discussed. Moreover, the improved magnetization distribution on the PM’s surface was made taking the PM’s relative permeability into account, and corresponding results have been given. These results indicated that the proposed method could help for a fast design and optimization of many PM devices that rely on magnetic forces, such as magnetic bearings, magnetic suspensions, magnetic actuators, etc.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15

Similar content being viewed by others

References

  1. Shetye, S.B., Agashe, J.S., Arnold, D.P.: Investigation of microscale magnetic forces for magnet array self-assembly. IEEE Trans. Magn. 43, 2713–2715 (2007). https://doi.org/10.1109/TMAG.2007.893707

    Article  ADS  Google Scholar 

  2. Abbes, M., Belharet, K., Mekki, H., Poisson, G.: Permanent magnets based actuator for microrobots navigation. IEEE Int. Conf. Intell. Robots Syst. 7062–7067 (2019). https://doi.org/10.1109/IROS40897.2019.8968558

  3. Kim, S.H., Shin, K.S., Hashi, S., Ishiyama, K.: A pushing force mechanism of magnetic spiral-type machine for wireless medical-robots in therapy and diagnosis. IEEE Trans. Magn. 49, 3488–3491 (2013). https://doi.org/10.1109/TMAG.2012.2237544

    Article  ADS  Google Scholar 

  4. Hou, M.T., Shen, H.M., Jiang, G.L., Lu, C.N., Hsu, I.J., Yeh, J.A.: A rolling locomotion method for untethered magnetic microrobots. Appl. Phys. Lett. 96, 94–97 (2010). https://doi.org/10.1063/1.3291112

    Article  Google Scholar 

  5. Mahoney, A.W., Abbott, J.J.: Managing magnetic force applied to a magnetic device by a rotating dipole field. Appl. Phys. Lett. 99, 1–4 (2011). https://doi.org/10.1063/1.3644021

    Article  Google Scholar 

  6. Zhou, R., Yan, M., Guo, Y., Jin, J., Sun, F., Zhang, X., Oka, K.: Suspension characteristics of a zero-power permanent magnetic suspension system with flux path control. Int. J. Appl. Electromagnet Mech 63, 187–198 (2020). https://doi.org/10.3233/JAE-209008

    Article  Google Scholar 

  7. Yang, J., Wen, Y., Li, P., Dai, X., Li, M.: A broadband vibration energy harvester using magnetoelectric transducer. IEEE SENSORS 2010 Conf. 1905–1909 (2010)

  8. Park, Y., Kim, H., Jang, H., Ham, S.H., Lee, J., Jung, D.H.: Efficiency improvement of permanent magnet BLDC with Halbach magnet array for drone. IEEE Trans. Appl. Supercond. 30, (2020). https://doi.org/10.1109/TASC.2020.2971672

  9. Hemeida, A., Hannon, B., Vansompel, H., Sergeant, P.: Comparison of three analytical methods for the precise calculation of cogging torque and torque ripple in axial flux PM machines. Math. Probl. Eng. 2016, (2016). https://doi.org/10.1155/2016/2171547

  10. Lubin, T., Rezzoug, A.: Steady-state and transient performance of axial-field eddy-current coupling. IEEE Trans. Industr. Electron. 62, 2287–2296 (2015). https://doi.org/10.1109/TIE.2014.2351785

    Article  Google Scholar 

  11. Mohammadi, S., Mirsalim, M., Vaez-Zadeh, S., Talebi, H.A.: Analytical modeling and analysis of axial-flux interior permanent-magnet couplers. IEEE Trans. Industr. Electron. 61, 5940–5947 (2014). https://doi.org/10.1109/TIE.2014.2311391

    Article  Google Scholar 

  12. Tian, M., Wang, X., Zhao, W., Yang, Y., Diao, J., Ma, X.: Analysis on a novel flux adjustable permanent magnet eddy current coupler with a double-layer permanent magnet rotor. IEEE Trans. Magn. 54, (2018). https://doi.org/10.1109/INTMAG.2018.8508584

  13. Jansen, J.W., Van Lierop, C.M.M., Lomonova, E.A., Vandenput, A.J.A.: Ironless magnetically levitated planar actuator. J. Appl. Phys. 103, 1–4 (2008). https://doi.org/10.1063/1.2832310

    Article  Google Scholar 

  14. Dieppedale, C., Desloges, B., Rostaing, H., Delamare, J., Cugat, O., Meunier-Carus, J.: Magnetic bistable micro-actuator with integrated permanent magnets. Proceedings of IEEE Sensors. 1, 493–496 (2004). https://doi.org/10.1109/icsens.2004.1426208

    Article  Google Scholar 

  15. Busch-Vishniac, I.J.: The case for magnetically driven microactuators. Sens. Actuators, A 33, 207–220 (1992). https://doi.org/10.1016/0924-4247(92)80168-3

    Article  Google Scholar 

  16. Allag, H., Yonnet, J.P.: 3-D analytical calculation of the torque and force exerted between two cuboidal magnets. IEEE Trans. Magn. 45, 3969–3972 (2009). https://doi.org/10.1109/TMAG.2009.2025047

    Article  ADS  Google Scholar 

  17. Akoun, G., Yonnet, J.P.: 3D analytical calculation of the forces exerted between two cuboidal magnets. IEEE Trans. Magn. 20, 1962–1964 (1984). https://doi.org/10.1109/TMAG.1984.1063554

    Article  ADS  Google Scholar 

  18. Rovers, J.M.M., Jansen, J.W., Lomonova, E.A., Ronde, M.J.C.: Calculation of the static forces among the permanent magnets in a halbach array. IEEE Trans. Magn. 45, 4372–4375 (2009). https://doi.org/10.1109/TMAG.2009.2021860

    Article  ADS  Google Scholar 

  19. Allag, H., Yonnet, J.P., Latreche, M.E.H.: Analytical calculation of the torque exerted between two perpendicularly magnetized magnets. J. Appl. Phys. 109, (2011). https://doi.org/10.1063/1.3535148

  20. Janssen, J.L.G., Paulides, J.J.H., Lomonova, E., Bölöni, F., Tounzi, A., Piriou, F.: Analytical calculation of interaction force between orthogonally magnetized permanent magnets. Sens. Lett. 7, 442–445 (2009). https://doi.org/10.1166/sl.2009.1049

    Article  Google Scholar 

  21. Allag, H., Yonnet, J.P., Fassenet, M., Latreche, M.E.: 3D analytical calculation of interactions between perpendicularly magnetized magnets-application to any magnetization direction. Sens. Lett. 7, 486–491 (2009). https://doi.org/10.1166/sl.2009.1094

    Article  Google Scholar 

  22. Yonnet, J.P., Allag, H.: Three-dimensional analytical calculation of permanent magnet interactions by “magnetic node” representation. IEEE Trans. Magn. 47, 2050–2055 (2011). https://doi.org/10.1109/TMAG.2011.2122339

    Article  ADS  Google Scholar 

  23. Lebedev, A.V., Lomonova, E.A., Van Leuven, P.G., Steinberg, J., Laro, D.A.H.: Analysis and initial synthesis of a novel linear actuator with active magnetic suspension. Conference Record - IAS Annual Meeting IEEE Industry Applications Society. 3, 2111–2118 (2004). https://doi.org/10.1109/ias.2004.1348758

    Article  Google Scholar 

  24. Lai, Y.C., Lee, Y.L., Yen, J.Y.: Design and servo control of a single-deck planar maglev stage. IEEE Trans. Magn. 43, 2600–2602 (2007). https://doi.org/10.1109/TMAG.2007.893530

    Article  ADS  Google Scholar 

  25. Lahdo, M., Strohla, T., Kovalev, S.: Repulsive magnetic levitation force calculation for a high precision 6-DoF magnetic levitation positioning system. IEEE Trans. Magn. 53, 2–7 (2017). https://doi.org/10.1109/TMAG.2016.2636124

    Article  Google Scholar 

  26. Furlani, E.P.: A formula for the levitation force between magnetic disks. IEEE Trans. Magn. 29, 4165–4169 (1993). https://doi.org/10.1109/20.280867

    Article  ADS  Google Scholar 

  27. Janssen, J.L.G., Paulides, J.J.H., Compter, J.C., Lomonova, E.A.: Three-dimensional analytical calculation of the torque between permanent magnets in magnetic bearings. IEEE Trans. Magn. 46, 1748–1751 (2010). https://doi.org/10.1109/TMAG.2010.2043224

    Article  ADS  Google Scholar 

  28. McCurrie, R.A.: Ferromagnetic Materials. Academic Press, London, U.K. (1994)

    Google Scholar 

  29. Jansen, J.W., Van Lierop, C.M.M., Lomonova, E.A., Vandenput, A.J.A.: Modeling of magnetically levitated planar actuators with moving magnets. IEEE Trans. Magn. 43, 15–25 (2007). https://doi.org/10.1109/TMAG.2006.886051

    Article  ADS  Google Scholar 

Download references

Funding

This work was supported by the Natural Science Foundation of Jilin Province (grant number 20170101060JC) and the Graduate Innovation Fund of Jilin University.

Author information

Authors and Affiliations

  1. Key Laboratory of CNC Equipment Reliability, Ministry of Education, School of Mechanical and Aerospace Engineering, Jilin University, Changchun, Jilin, 130022, China

    Chuan Qu, Yong-Chen Pei & Zhen-Xing Li

Authors
  1. Chuan Qu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yong-Chen Pei
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Zhen-Xing Li
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yong-Chen Pei.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Qu, C., Pei, YC. & Li, ZX. A Study on Magnetic Force Characteristics Between Two Cuboidal Permanent Magnets. J Supercond Nov Magn 34, 2441–2454 (2021). https://doi.org/10.1007/s10948-021-05927-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10948-021-05927-6

Keywords

Search

Navigation