Skip to main content
SpringerLink
Log in

A Modified Convective Formulation in Navier–Stokes Simulations

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

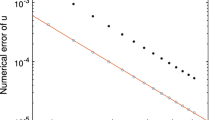
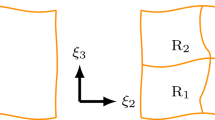
Abstract

For the discretization of the convective term in the Navier–Stokes equations, the commonly used convective formulation (CONV) does not preserve kinetic energy if the divergence constraint is only discretely enforced. In this paper, we apply the skew-symmetrization technique in Cockburn et al. (Math Comput 74(251):1067–1095, 2005. https://doi.org/10.1090/S0025-5718-04-01718-1) to conforming finite element methods, which restores energy conservation for CONV. The main idea is to replace the discrete advective velocity with an \(H({\text {div}})\)-conforming divergence-free one in CONV. We prove that the modified convective formulation also conserves linear momentum, helicity, 2D enstrophy and total vorticity under some appropriate senses. The popular CNLE (linearly extrapolated Crank–Nicolson) method also conserves them when this modified formulation is used. Under the assumption \(\varvec{u}\in L^{2}(0,T;\varvec{W}^{1,\infty }(\Omega )),\) it can be shown that the Gronwall constant does not explicitly depend on the Reynolds number in the error estimates. Numerical experiments show that the linearized and modified convective formulation has similar performance with the EMAC formulation and outperforms the usual skew-symmetric formulation (SKEW).

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

Data Availability

All data generated or analysed during this study are included in this manuscript. Partial work was completed during the first author’s visit at Weierstrass Institute, 10117 Berlin, Germany.

References

  1. Evans, J.A., Hughes, T.J.R.: Isogeometric divergence-conforming B-splines for the unsteady Navier-Stokes equations. J. Comput. Phys. 241, 141–167 (2013). https://doi.org/10.1016/j.jcp.2013.01.006

    Article  MathSciNet  MATH  Google Scholar 

  2. Charnyi, S., Heister, T., Olshanskii, M.A., Rebholz, L.G.: On conservation laws of Navier–Stokes Galerkin discretizations. J. Comput. Phys. 337, 289–308 (2017). https://doi.org/10.1016/j.jcp.2017.02.039

    Article  MathSciNet  MATH  Google Scholar 

  3. Arakawa, A.: Computational design for long-term numerical integration of the equations of fluid motion: two dimensional incompressible flow. Part I. J. Comput. Phys. 1, 119–143 (1966). https://doi.org/10.1016/0021-9991(66)90015-5

    Article  MATH  Google Scholar 

  4. Fix, G.J.: Finite element models for ocean circulation problems. SIAM J. Appl. Math. 29(3), 371–387 (1975). https://doi.org/10.1137/0129031

    Article  MathSciNet  MATH  Google Scholar 

  5. Abramov, R.V., Majda, A.J.: Discrete approximations with additional conserved quantities: deterministic and statistical behavior. Methods Appl. Anal. 10(2), 151–190 (2003). https://doi.org/10.4310/MAA.2003.v10.n2.a1

    Article  MathSciNet  MATH  Google Scholar 

  6. Rebholz, L.G.: An energy- and helicity-conserving finite element scheme for the Navier–Stokes equations. SIAM J. Numer. Anal. 45(4), 1622–1638 (2007). https://doi.org/10.1137/060651227

    Article  MathSciNet  MATH  Google Scholar 

  7. Palha, A., Gerritsma, M.: A mass, energy, enstrophy and vorticity conserving (MEEVC) mimetic spectral element discretization for the 2D incompressible Navier-Stokes equations. J. Comput. Phys. 328, 200–220 (2017). https://doi.org/10.1016/j.jcp.2016.10.009

    Article  MathSciNet  MATH  Google Scholar 

  8. Olshanskii, M.A., Rebholz, L.G.: Longer time accuracy for incompressible Navier–Stokes simulations with the EMAC formulation. Comput. Methods Appl. Mech. Engrg. 372, 113369 (2020). https://doi.org/10.1016/j.cma.2020.113369

    Article  MathSciNet  MATH  Google Scholar 

  9. John, V., Linke, A., Merdon, C., Neilan, M., Rebholz, L.G.: On the divergence constraint in mixed finite element methods for incompressible flows. SIAM Rev. 59(3), 492–544 (2017). https://doi.org/10.1137/15M1047696

    Article  MathSciNet  MATH  Google Scholar 

  10. Pastrana, D., Cajas, J.C., Lehmkuhl, O., Rodríguez, I., Houzeaux, G.: Large-eddy simulations of the vortex-induced vibration of a low mass ratio two-degree-of-freedom circular cylinder at subcritical reynolds numbers. Comput. Fluids 173, 118–132 (2018). https://doi.org/10.1016/j.compfluid.2018.03.016

    Article  MathSciNet  MATH  Google Scholar 

  11. Lehmkuhl, O., Houzeaux, G., Owen, H., Chrysokentis, G., Rodriguez, I.: A low-dissipation finite element scheme for scale resolving simulations of turbulent flows. J. Comput. Phys. 390, 51–65 (2019). https://doi.org/10.1016/j.jcp.2019.04.004

    Article  MathSciNet  MATH  Google Scholar 

  12. Owen, H., Chrysokentis, G., Avila, M., Mira, D., Houzeaux, G., Borrell, R., Cajas, J.C., Lehmkuhl, O.: Wall-modeled large-eddy simulation in a finite element framework. Int. J. Numer. Methods Fluids 92(1), 20–37 (2020). https://doi.org/10.1002/fld.4770

    Article  MathSciNet  Google Scholar 

  13. Ingram, R.: A new linearly extrapolated Crank-Nicolson time-stepping scheme for the Navier–Stokes equations. Math. Comput. 82(284), 1953–1973 (2013). https://doi.org/10.1090/S0025-5718-2013-02678-6

    Article  MathSciNet  MATH  Google Scholar 

  14. Layton, W., Manica, C.C., Neda, M., Rebholz, L.G.: Numerical analysis and computational testing of a high accuracy Leray-deconvolution model of turbulence. Numer. Methods Part. Differe. Eq. 24(2), 555–582 (2008). https://doi.org/10.1002/num.20281

    Article  MathSciNet  MATH  Google Scholar 

  15. Labovsky, A., Layton, W.J., Manica, C.C., Neda, M., Rebholz, L.G.: The stabilized extrapolated trapezoidal finite-element method for the Navier–Stokes equations. Comput. Methods Appl. Mech. Engrg. 198(9), 958–974 (2009). https://doi.org/10.1016/j.cma.2008.11.004

    Article  MathSciNet  MATH  Google Scholar 

  16. He, Y., Sun, W.: Stabilized finite element method based on the Crank-Nicolson extrapolation scheme for the time-dependent Navier–Stokes equations. Math. Comp. 76(257), 115–137 (2007). https://doi.org/10.1090/S0025-5718-06-01886-2

    Article  MathSciNet  MATH  Google Scholar 

  17. Charnyi, S., Heister, T., Olshanskii, M.A., Rebholz, L.G.: Efficient discretizations for the EMAC formulation of the incompressible Navier–Stokes equations. Appl. Numer. Math. 141, 220–233 (2019). https://doi.org/10.1016/j.apnum.2018.11.013

    Article  MathSciNet  MATH  Google Scholar 

  18. Cockburn, B., Kanschat, G., Schötzau, D.: A locally conservative LDG method for the incompressible Navier–Stokes equations. Math. Comput. 74(251), 1067–1095 (2005). https://doi.org/10.1090/S0025-5718-04-01718-1

    Article  MathSciNet  MATH  Google Scholar 

  19. Guzmán, J., Shu, C.-W., Sequeira, F.A.: H(div) conforming and DG methods for incompressible Euler’s equations. IMA J. Numer. Anal. 37, 1733–1771 (2017). https://doi.org/10.1093/imanum/drw054

    Article  MathSciNet  MATH  Google Scholar 

  20. Lederer, P.L., Lehrenfeld, C., Schöberl, J.: Hybrid discontinuous Galerkin methods with relaxed H(div)-conformity for incompressible flows. Part II. ESAIM Math. Model. Numer. Anal. 53(2), 503–522 (2019). https://doi.org/10.1051/m2an/2018054

    Article  MathSciNet  MATH  Google Scholar 

  21. Matthies, G., Tobiska, L.: Mass conservation of finite element methods for coupled flow-transport problems. Int. J. Comput. Sci. Math. 1(2/3/4), 293 (2007). https://doi.org/10.1504/IJCSM.2007.016537

    Article  MathSciNet  MATH  Google Scholar 

  22. Gmeiner, B., Waluga, C., Wohlmuth, B.: Local mass-corrections for continuous pressure approximations of incompressible flow. SIAM J. Numer. Anal. 52(6), 2931–2956 (2014). https://doi.org/10.1137/140959675

    Article  MathSciNet  MATH  Google Scholar 

  23. Linke, A.: On the role of the Helmholtz decomposition in mixed methods for incompressible flows and a new variational crime. Comput. Methods Appl. Mech. Engrg. 268, 782–800 (2014). https://doi.org/10.1016/j.cma.2013.10.011

    Article  MathSciNet  MATH  Google Scholar 

  24. Linke, A., Matthies, G., Tobiska, L.: Robust arbitrary order mixed finite element methods for the incompressible Stokes equations with pressure independent velocity errors. ESAIM Math. Model. Numer. Anal. 50(1), 289–309 (2016). https://doi.org/10.1051/m2an/2015044

    Article  MathSciNet  MATH  Google Scholar 

  25. Lederer, P.L., Linke, A., Merdon, C., Schöberl, J.: Divergence-free reconstruction operators for pressure-robust Stokes discretizations with continuous pressure finite elements. SIAM J. Numer. Anal. 55(3), 1291–1314 (2017). https://doi.org/10.1137/16M1089964

    Article  MathSciNet  MATH  Google Scholar 

  26. Allendes, A., Barrenechea, G.R., Naranjo, C.: A divergence-free low-order stabilized finite element method for a generalized steady state Boussinesq problem. Comput. Methods Appl. Mech. Engrg. 340, 90–120 (2018). https://doi.org/10.1016/j.cma.2018.05.020

    Article  MathSciNet  MATH  Google Scholar 

  27. Allendes, A., Barrenechea, G.R., Novo, J.: A divergence-free stabilized finite element method for the evolutionary Navier-Stokes equations. SIAM J. Sci. Comput. 43(6), 3809–3836 (2021). https://doi.org/10.1137/21M1394709

    Article  MathSciNet  MATH  Google Scholar 

  28. García-Archilla, B., John, V., Novo, J.: On the convergence order of the finite element error in the kinetic energy for high Reynolds number incompressible flows. Comput. Methods Appl. Mech. Engrg. 385, 114032 (2021). https://doi.org/10.1016/j.cma.2021.114032

    Article  MathSciNet  MATH  Google Scholar 

  29. Schroeder, P.W., Lehrenfeld, C., Linke, A., Lube, G.: Towards computable flows and robust estimates for inf-sup stable FEM applied to the time-dependent incompressible Navier-Stokes equations. SeMA 75(4), 629–653 (2018). https://doi.org/10.1007/s40324-018-0157-1

    Article  MathSciNet  MATH  Google Scholar 

  30. John, V., Knobloch, P., Novo, J.: Finite elements for scalar convection-dominated equations and incompressible flow problems: a never ending story? Comput. Visual Sci. 19(5–6), 47–63 (2018). https://doi.org/10.1007/s00791-018-0290-5

    Article  MathSciNet  MATH  Google Scholar 

  31. Bernardi, C., Raugel, G.: Analysis of some finite elements for the Stokes problem. Math. Comp. 44(169), 71–79 (1985). https://doi.org/10.2307/2007793

    Article  MathSciNet  MATH  Google Scholar 

  32. Girault, V., Raviart, P.-A.: Finite element methods for Navier–Stokes equations. Springer series in computational mathematics, vol. 5. Springer, Berlin (1986). https://doi.org/10.1007/978-3-642-61623-5

  33. Boffi, D., Brezzi, F., Fortin, M.: Mixed finite element methods and applications. Springer Series in Computational Mathematics, vol. 44. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-36519-5

  34. Olshanskii, M., Rebholz, L.G.: Note on helicity balance of the Galerkin method for the 3D Navier–Stokes equations. Comput. Methods Appl. Mech. Eng. 199(17), 1032–1035 (2010). https://doi.org/10.1016/j.cma.2009.11.015

    Article  MathSciNet  MATH  Google Scholar 

  35. Girault, V., Nochetto, R.H., Scott, L.R.: Max-norm estimates for Stokes and Navier–Stokes approximations in convex polyhedra. Numer. Math. 131(4), 771–822 (2015). https://doi.org/10.1007/s00211-015-0707-8

    Article  MathSciNet  MATH  Google Scholar 

  36. Olshanskii, M.A.: A low order Galerkin finite element method for the Navier–Stokes equations of steady incompressible flow: a stabilization issue and iterative methods. Comput. Methods Appl. Mech. Engrg. 191(47), 5515–5536 (2002). https://doi.org/10.1016/S0045-7825(02)00513-3

    Article  MathSciNet  MATH  Google Scholar 

  37. Olshanskii, M.A., Reusken, A.: Grad-div stabilization for Stokes equations. Math. Comput. 73, 1699–1718 (2004). https://doi.org/10.1090/S0025-5718-03-01629-6

    Article  MathSciNet  MATH  Google Scholar 

  38. de Frutos, J., García-Archilla, B., John, V., Novo, J.: Analysis of the grad-div stabilization for the time-dependent Navier–Stokes equations with inf-sup stable finite elements. Adv. Comput. Math. 44(1), 195–225 (2018). https://doi.org/10.1007/s10444-017-9540-1

    Article  MathSciNet  MATH  Google Scholar 

  39. John, V., Li, X., Merdon, C., Rui, H.: Inf-sup stabilized Scott–Vogelius pairs on general simplicial grids by Raviart–Thomas enrichment. arXiv: 2206.01242 (2022). https://doi.org/10.48550/ARXIV.2206.01242

  40. Li, Xu., Rui, H.: An EMA-conserving, pressure-robust and Re-semi-robust method with a robust reconstruction method for Navier-Stokes. ESAIM Math. Model. Numer. Anal. 57(2), 467–490 (2023). https://doi.org/10.1051/m2an/2022093

    Article  MathSciNet  MATH  Google Scholar 

  41. Linke, A., Merdon, C.: Pressure-robustness and discrete Helmholtz projectors in mixed finite element methods for the incompressible Navier-Stokes equations. Comput. Methods Appl. Mech. Engrg. 311, 304–326 (2016). https://doi.org/10.1016/j.cma.2016.08.018

    Article  MathSciNet  MATH  Google Scholar 

  42. Li, X., Rui, H.: A low-order divergence-free H(div)-conforming finite element method for Stokes flows. IMA J. Numer. Anal. 42(4), 3711–3734 (2021). https://doi.org/10.1093/imanum/drab080

    Article  MathSciNet  MATH  Google Scholar 

  43. Arnold, D.N., Qin, J.: Quadratic velocity/linear pressure Stokes elements. In: R. Vichnevetsky, D. Knight & G. Richter (eds). Advances in Computer Methods for Partial Differential Equations-VII, pp 28–34. IMACS, New Brunswick, NJ (1992)

  44. Gresho, P.: On the theory of semiimplicit projection methods for viscous incompressible flow and its implementation via a finite element method that also introduces a nearly consistent mass matrix, part 2: implementation. Int. J. Numer. Methods Fluids 11, 1 (1990). https://doi.org/10.1002/fld.1650110510

    Article  MathSciNet  Google Scholar 

  45. John, V., Liakos, A.: Time-dependent flow across a step: the slip with friction boundary condition. Int. J. Numer. Meth. Fluids 50(6), 713–731 (2006). https://doi.org/10.1002/fld.1074

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

We are very grateful to Ziyan Li from City University of Hong Kong for many valuable discussions on coding implementation.

Funding

This work was supported by the National Natural Science Foundation of China (Grant 12131014). The first author was also supported by the China Scholarship Council (Grant 202106220106).

Author information

Authors and Affiliations

  1. School of Mathematics, Shandong University, Jinan, 250100, China

    Xu Li & Hongxing Rui

Authors
  1. Xu Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Hongxing Rui
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Hongxing Rui.

Ethics declarations

Competing interests

The authors declare that they have no competing interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Li, X., Rui, H. A Modified Convective Formulation in Navier–Stokes Simulations. J Sci Comput 96, 69 (2023). https://doi.org/10.1007/s10915-023-02286-3

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10915-023-02286-3

Keywords

Mathematics Subject Classification

Search

Navigation