Skip to main content

Advertisement

SpringerLink
Log in

A High-Order Discrete Energy Decay and Maximum-Principle Preserving Scheme for Time Fractional Allen–Cahn Equation

  • Review
  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

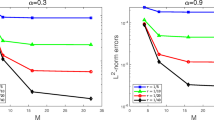
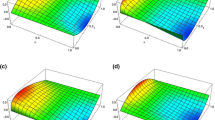
The shifted fractional trapezoidal rule (SFTR) with a special shift is adopted to construct a finite difference scheme for the time-fractional Allen–Cahn (tFAC) equation. Some essential key properties of the weights of SFTR are explored for the first time. Based on these properties, we rigorously demonstrate the discrete energy decay property and maximum-principle preservation for the scheme. Numerical investigations show that the scheme can resolve the intrinsic initial singularity of such nonlinear fractional equations as tFAC equation on uniform meshes without any correction. Comparison with the classic fractional BDF2 and L2-1\(_\sigma \) method further validates the superiority of SFTR in solving the tFAC equation. Experiments concerning both discrete energy decay and discrete maximum-principle also verify the correctness of the theoretical results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

Data Availability

The data that support the findings of this study are available from the corresponding author, upon reasonable request.

References

  1. Al-Maskari, M., Karaa, S.: The time-fractional Cahn-Hilliard equation: analysis and approximation. IMA J. Numer. Anal. 42(2), 1831–65 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  2. Alikhanov, A.A.: A new difference scheme for the time fractional diffusion equation. J. Comput. Phys. 280, 424–438 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  3. Allen, S.M., Cahn, J.W.: A microscopic theory for antiphase boundary motion and its application to antiphase domain coarsening. Acta Metall. 27(6), 1085–1095 (1979)

    Article  Google Scholar 

  4. Anderson, D.M., McFadden, G.B., Wheeler, A.A.: Diffuse-interface methods in fluid mechanics. Annu. Rev. Fluid Mech. 30(1), 139–165 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  5. Bu, W., Xiao, A., Zeng, W.: Finite difference/finite element methods for distributed-order time fractional diffusion equations. J. Sci. Comput. 72(1), 422–441 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  6. Chen, L., Zhang, J., Zhao, J., Cao, W., Wang, H., Zhang, J.: An accurate and efficient algorithm for the time-fractional molecular beam epitaxy model with slope selection. Comput. Phys. Commun. 245, 106842 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  7. Chen, S., Shen, J., Zhang, Z., Zhou, Z.: A spectrally accurate approximation to subdiffusion equations using the log orthogonal functions. SIAM J. Sci. Comput. 42(2), A849–A877 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  8. Du, Q., Yang, J., Zhou, Z.: Time-fractional Allen-Cahn equations: analysis and numerical methods. J. Sci. Comput. 85(2), 42 (2020)

  9. Gao, G., Sun, Z.: A compact finite difference scheme for the fractional sub-diffusion equations. J. Comput. Phys. 230(3), 586–595 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  10. Hou, D., Xu, C.: Highly efficient and energy dissipative schemes for the time fractional Allen-Cahn equation. SIAM J. Sci. Comput. 43(5), A3305–A3327 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  11. Hou, D., Xu, C.: A second order energy dissipative scheme for time fractional \(L^2\) gradient flows using SAV approach. J. Sci. Comput. 90(1), 25 (2022)

  12. Hou, D., Zhu, H., Xu, C.: Highly efficient schemes for time-fractional Allen-Cahn equation using extended SAV approach. Numer. Algorithm. 88, 1077–1108 (2021)

  13. Hou, T., Tang, T., Yang, J.: Numerical analysis of fully discretized Crank-Nicolson scheme for fractional-in-space Allen-Cahn equations. J. Sci. Comput. 72(3), 1214–1231 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  14. Huang, C., Stynes, M.: Optimal \(H^1\) spatial convergence of a fully discrete finite element method for the time-fractional Allen-Cahn equation. Adv. Comput. Math. 46(4), 63 (2020)

    Article  MATH  Google Scholar 

  15. Ji, B., Liao, H., Gong, Y., Zhang, L.: Adaptive linear second-order energy stable schemes for time-fractional Allen-Cahn equation with volume constraint. Commun. Nonlinear Sci. Numer. Simul. 90, 105366 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  16. Jia, J., Zhang, H., Xu, H., Jiang, X.: An efficient second order stabilized scheme for the two dimensional time fractional Allen-Cahn equation. Appl. Numer. Math. 165, 216–231 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  17. Jiang, S., Zhang, J., Zhang, Q., Zhang, Z.: Fast evaluation of the Caputo fractional derivative and its applications to fractional diffusion equations. Commun. Comput. Phys. 21(3), 650–678 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  18. Jin, B., Lazarov, R., Zhou, Z.: Numerical methods for time-fractional evolution equations with nonsmooth data: a concise overview. Comput. Methods Appl. Mech. Engrg. 346, 332–358 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  19. Jin, B., Li, B., Zhou, Z.: Numerical analysis of nonlinear subdiffusion equations. SIAM J. Numer. Anal. 56(1), 1–23 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  20. Kopteva, N.: Error analysis of the L1 method on graded and uniform meshes for a fractional-derivative problem in two and three dimensions. Math. Comp. 88(319), 2135–2155 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  21. Li, C., Yi, Q.: Finite difference method for two-dimensional nonlinear time-fractional subdiffusion equation. Fract. Calc. Appl. Anal. 21(4), 1046–1072 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  22. Li, D., Sun, W., Wu, C.: A novel numerical approach to time-fractional parabolic equations with nonsmooth solutions. Numer. Math. Theory Methods Appl. 14(2), 355–376 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  23. Li, D., Zhang, J., Zhang, Z.: Unconditionally optimal error estimates of a linearized Galerkin method for nonlinear time fractional reaction-subdiffusion equations. J. Sci. Comput. 76(2), 848–866 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  24. Li, M., Zhao, J., Huang, C., Chen, S.: Nonconforming virtual element method for the time fractional reaction-subdiffusion equation with non-smooth data. J. Sci. Comput. 81(3), 1823–1859 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  25. Li, M., Zhao, J., Huang, C., Chen, S.: Conforming and nonconforming VEMs for the fourth-order reaction-subdiffusion equation: a unified framework. IMA J. Numer. Anal. 42(3), 2238–300 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  26. Liao, H., Tang, T., Zhou, T.: A second-order and nonuniform time-stepping maximum-principle preserving scheme for time-fractional Allen-Cahn equations. J. Comput. Phys. 414, 109473 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  27. Liao, H., Tang, T., Zhou, T.: An energy stable and maximum bound preserving scheme with variable time steps for time fractional Allen-Cahn equation. SIAM J. Sci. Comput. 43(5), A3503–A3526 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  28. Liao, H., Zhu, X., Wang, J.: The variable-step L1 scheme preserving a compatible energy law for time-fractional Allen-Cahn equation. Numer. Math. Theor. Meth. Appl. 15(4), 1128–1146 (2022)

  29. Liu, F., Yang, C., Burrage, K.: Numerical method and analytical technique of the modified anomalous subdiffusion equation with a nonlinear source term. J. Comput. Appl. Math. 231(1), 160–176 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  30. Liu, H., Cheng, A., Wang, H., Zhao, J.: Time-fractional Allen-Cahn and Cahn-Hilliard phase-field models and their numerical investigation. Comput. Math. Appl. 76(8), 1876–1892 (2018)

    MathSciNet  MATH  Google Scholar 

  31. Liu, Y., Yin, B., Li, H., Zhang, Z.: The unified theory of shifted convolution quadrature for fractional calculus. J. Sci. Comput. 89(1), 18 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  32. Lubich, C.: Discretized fractional calculus. SIAM J. Math. Anal. 17(3), 704–719 (1986)

    Article  MathSciNet  MATH  Google Scholar 

  33. Mohebbi, A., Abbaszadeh, M., Dehghan, M.: A high-order and unconditionally stable scheme for the modified anomalous fractional sub-diffusion equation with a nonlinear source term. J. Comput. Phys. 240, 36–48 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  34. Quan, C., Tang, T., Yang, J.: How to define dissipation-preserving energy for time-fractional phase-field equations. CSIAM Tran. Appl. Math. 1(3), 478–490 (2020)

  35. Shao, D., Rappel, W.J., Levine, H.: Computational model for cell morphodynamics. Phys. Rev. Lett. 105(10), 108104 (2010)

    Article  Google Scholar 

  36. Shen, J., Tang, T., Yang, J.: On the maximum principle preserving schemes for the generalized Allen-Cahn equation. Commun. Math. Sci. 14(6), 1517–1534 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  37. Stynes, M.: Too much regularity may force too much uniqueness. Fract. Calc. Appl. Anal. 19(6), 1554–1562 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  38. Stynes, M., O’Riordan, E., Gracia, J.L.: Error analysis of a finite difference method on graded meshes for a time-fractional diffusion equation. SIAM J. Numer. Anal. 55(2), 1057–1079 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  39. Tang, T., Yu, H., Zhou, T.: On energy dissipation theory and numerical stability for time-fractional phase-field equations. SIAM J. Sci. Comput. 41(6), A3757–A3778 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  40. Xu, C., Prince, J.L.: Snakes, shapes, and gradient vector flow. IEEE Trans. Image Process. 7(3), 359–369 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  41. Yin, B., Liu, Y., Li, H.: Necessity of introducing non-integer shifted parameters by constructing high accuracy finite difference algorithms for a two-sided space-fractional advection-diffusion model. Appl. Math. Lett. 105, 106347 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  42. Yin, B., Liu, Y., Li, H., Zhang, Z.: Two families of second-order fractional numerical formulas and their applications to fractional differential equations. Fract. Calc. Appl. Anal. (2023). https://doi.org/10.1007/s13540-023-00172-1

  43. Yin, B., Liu, Y., Li, H., Zhang, Z.: Efficient shifted fractional trapezoidal rule for subdiffusion problems with nonsmooth solutions on uniform meshes. BIT Numer. Math. 62(2), 631–66 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  44. Zhang, H., Yang, X., Xu, D.: An efficient spline collocation method for a nonlinear fourth-order reaction subdiffusion equation. J. Sci. Comput. 85(1), 7 (2020)

  45. Zhao, J., Xiao, J., Ford, N.J.: Collocation methods for fractional integro-differential equations with weakly singular kernels. Numer. Algorithm. 65(4), 723–743 (2014)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The authors are grateful to two anonymous referees and editors for their valuable suggestions which improve the presentation of this work greatly.

Funding

This work is supported by the Natural Science Foundation of Inner Mongolia Autonomous Region of China (No. 2021BS01003 to G.Z.), NSF of China (Nos. 12171177 and 12011530058 to C.H., 12201322 to B.Y.).

Author information

Authors and Affiliations

  1. School of Mathematical Sciences, Inner Mongolia University, Hohhot, 010021, China

    Guoyu Zhang & Baoli Yin

  2. School of Mathematics and Statistics, Huazhong University of Science and Technology, Wuhan, 430074, China

    Chengming Huang

  3. Hubei Key Laboratory of Engineering Modeling and Scientific Computing, Huazhong University of Science and Technology, Wuhan, 430074, China

    Chengming Huang

  4. North-Caucasus Center for Mathematical Research, North-Caucasus Federal University, Stavropol, 355017, Russia

    Anatoly A. Alikhanov

Authors
  1. Guoyu Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Chengming Huang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Anatoly A. Alikhanov
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Baoli Yin
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Guoyu Zhang.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhang, G., Huang, C., Alikhanov, A.A. et al. A High-Order Discrete Energy Decay and Maximum-Principle Preserving Scheme for Time Fractional Allen–Cahn Equation. J Sci Comput 96, 39 (2023). https://doi.org/10.1007/s10915-023-02263-w

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10915-023-02263-w

Keywords

Search

Navigation