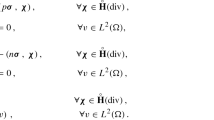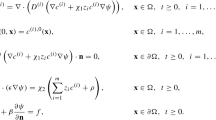Skip to main content
SpringerLink
Log in

Optimal Error Estimates of Coupled and Divergence-Free Virtual Element Methods for the Poisson–Nernst–Planck/Navier–Stokes Equations and Applications in Electrochemical Systems

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

In this article, we propose and analyze a fully coupled, nonlinear, and energy-stable virtual element method (VEM) for solving the coupled Poisson–Nernst–Planck (PNP) and Navier–Stokes (NS) equations. These equations model microfluidic and electrochemical systems that include the diffuse transport of charged species within incompressible fluids coupled through electrostatic forces. A mixed VEM is employed to discretize the NS equations whereas classical VEM in primal form is used to discretize the PNP equations. The stability, existence and uniqueness of solution of the associated VEM are proved by fixed point theory. The global mass conservation and electric energy decay of the scheme are also established. Also, we rigorously derive unconditionally optimal error estimates for both the electrostatic potential and ionic concentrations of PNP equations in the \(\textrm{L}^{2}\) and \(\textrm{H}^{1}\)-norms, as well as for the velocity and pressure of NS equations in the \(\textbf{L}^{2}\), \(\textbf{H}^1\)- and \(\textrm{L}^{2}\)-norms, respectively. Finally, several numerical experiments are presented to support the theoretical analysis of convergence and to illustrate the satisfactory performance of the method in simulating the onset of electrokinetic instabilities in ionic fluids, and studying how they are influenced by different values of ion concentration and applied voltage. These tests are relevant in applications of water desalination.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

Data Availability

Data sharing not applicable to this article as no datasets were generated or analysed during the current study.

References

  1. Ahmad, B., Alsaedi, A., Brezzi, F., Marini, L.D., Russo, A.: Equivalent projectors for virtual element methods. Comput. Math. Appl. 66(3), 376–391 (2013)

    MathSciNet  MATH  Google Scholar 

  2. Beirão da Veiga, L., Brezzi, F., Cangiani, A., Manzini, G., Marini, L.D., Russo, A.: Basic principles of virtual element methods. Math. Models Methods Appl. Sci. 23, 199–214 (2013)

    MathSciNet  MATH  Google Scholar 

  3. Beirão da Veiga, L., Brezzi, F., Marini, L.D., Russo, A.: The Hitchhiker’s guide to the virtual element method. Math. Models Methods Appl. Sci. 24(8), 1541–1573 (2014)

    MathSciNet  MATH  Google Scholar 

  4. Beirão da Veiga, L., Lovadina, C., Russo, A.: Stability analysis for the virtual element method. Math. Models Methods Appl. Sci. 27(13), 2557–2594 (2017)

    MathSciNet  MATH  Google Scholar 

  5. Beirão da Veiga, L., Lovadina, C., Vacca, G.: Divergence free virtual elements for the Stokes problem on polygonal meshes. ESAIM Math. Model. Numer. Anal. 51(2), 509–535 (2017)

    MathSciNet  MATH  Google Scholar 

  6. Beirão da Veiga, L., Lovadina, C., Vacca, G.: Virtual elements for the Navier–Stokes problem on polygonal meshes. SIAM J. Numer. Anal. 56(3), 1210–1242 (2018)

    MathSciNet  MATH  Google Scholar 

  7. Beirão da Veiga, L., Mora, D., Vacca, G.: The Stokes complex for virtual elements with application to Navier–Stokes flows. J. Sci. Comput. 81(2), 990–1018 (2019)

    MathSciNet  MATH  Google Scholar 

  8. Brenner, S.C., Guan, Q., Sung, L.Y.: Some estimates for virtual element methods. Comput. Methods Appl. Math. 17(4), 553–574 (2017)

    MathSciNet  MATH  Google Scholar 

  9. Brezzi, F., Falk, R.S., Marini, L.D.: Basic principles of mixed virtual element methods. ESAIM Math. Model. Numer. Anal. 48(4), 1227–1240 (2014)

    MathSciNet  MATH  Google Scholar 

  10. Bürger, R., Méndez, P.E., Ruiz-Baier, R.: On H(div)-conforming methods for double-diffusion equations in porous media. SIAM J. Numer. Anal. 57(3), 1318–1343 (2019)

    MathSciNet  MATH  Google Scholar 

  11. Cáceres, E., Gatica, G.N.: A mixed virtual element method for the pseudostress-velocity formulation of the Stokes problem. IMA J. Numer. Anal. 37(1), 296–331 (2017)

    MathSciNet  MATH  Google Scholar 

  12. Cangiani, A., Gyrya, V., Manzini, G.: The nonconforming virtual element method for the Stokes equations. SIAM J. Numer. Anal. 54(6), 3411–3435 (2016)

    MathSciNet  MATH  Google Scholar 

  13. Cangiani, A., Manzini, G., Sutton, O.J.: Conforming and nonconforming virtual element methods for elliptic problems. IMA J. Numer. Anal. 37(3), 1317–1354 (2017)

    MathSciNet  MATH  Google Scholar 

  14. Chen, L., Huang, J.: Some error analysis on virtual element methods. Calcolo 55(1), 23 (2018)

    MathSciNet  MATH  Google Scholar 

  15. Choi, H., Paraschivoiu, M.: Advanced hybrid-flux approach for output bounds of electroosmotic flows: adaptive refinement and direct equilibrating strategies. Microfluid. Nanofluid. 2(2), 154–170 (2005)

    Google Scholar 

  16. Cioffi, M., Boschetti, F., Raimondi, M.T., Dubini, G.: Modeling evaluation of the fluiddynamic microenvironment in tissue-engineered constructs: a micro-CT based model. Biotechnol. Bioeng. 93(3), 500–510 (2006)

    Google Scholar 

  17. Correa, C.I., Gatica, G.N., Ruiz-Baier, R.: New mixed finite element methods for the coupled Stokes/Poisson–Nernst–Planck equations in Banach spaces. CI\(^2\)MA preprint (2022). Available from https://www.ci2ma.udec.cl/publicaciones

  18. Correa, C.I., Gatica, G.N., Ruiz-Baier, R.: Banach spaces-based mixed finite element methods for the coupled Navier–Stokes and Poisson–Nernst–Planck equations. CI\(^2\)MA preprint (2023). Available from https://www.ci2ma.udec.cl/publicaciones

  19. Dehghan, M., Gharibi, Z.: Virtual element method for solving an inhomogeneous Brusselator model with and without cross-diffusion in pattern formation. J. Sci. Comput. 89(1), 16 (2021)

    MathSciNet  MATH  Google Scholar 

  20. Dreyer, W., Guhlke, C., Müller, R.: Overcoming the shortcomings of the Nernst–Planck model. Phys. Chem. Chem. Phys. 15(19), 7075–7086 (2013)

    Google Scholar 

  21. Druzgalski, C., Andersen, M., Mani, A.: Direct numerical simulation of electroconvective instability and hydrodynamic chaos near an ion-selective surface. Phys. Fluids 25, 110804 (2013)

    Google Scholar 

  22. Evans, L.C.: Partial Differential Equations, 2nd edn. American Mathematical Society, Providence (2010)

    MATH  Google Scholar 

  23. Fuhrmann, J., Guhlke, C., Merdon, C., Linke, A., Müller, R.: Induced charge electroosmotic flow with finite ion size and solvation effects. Electrochimica Acta 317, 778–785 (2019)

    MATH  Google Scholar 

  24. Fuhrmann, J., Guhlke, C., Linke, A., Merdon, C., Müller, R.: Models and numerical methods for electrolyte flows. In: Hintermüller, M., Rodrigues, J.F. (eds.) Topics in Applied Analysis and Optimisation, CIM Series in Mathematical Sciences, pp. 183–209. Springer, Berlin (2019)

    MATH  Google Scholar 

  25. Gao, H., He, D.: Linearized conservative finite element methods for the Nernst–Planck–Poisson equations. J. Sci. Comput. 72, 1269–1289 (2017)

    MathSciNet  MATH  Google Scholar 

  26. Gao, H., Sun, P.: A linearized local conservative mixed finite element method for Poisson–Nernst–Planck equations. J. Sci. Comput. 77, 793–817 (2018)

    MathSciNet  MATH  Google Scholar 

  27. Gatica, G.N., Munar, M., Sequeira, F.: A mixed virtual element method for the Navier–Stokes equations. Math. Models Methods Appl. Sci. 28(14), 2719–2762 (2018)

    MathSciNet  MATH  Google Scholar 

  28. Gross, A., Morvezen, A., Castillo, P., Xu, X., Xu, P.: Numerical investigation of the effect of two-dimensional surface waviness on the current density of ion-selective membranes for electrodialysis. Water 11(7), 1397 (2019)

    Google Scholar 

  29. Galama, O.: Ion exchange membranes in seawater applications: processes and characteristics. Ph.D Thesis (2015)

  30. Gharibi, Z., Dehghan, M., Abbaszadeh, M.: Numerical analysis of locally conservative weak Galerkin dual-mixed finite element method for the time-dependent Poisson–Nernst–Planck system. Comput. Math. Appl. 92, 88–108 (2021)

    MathSciNet  MATH  Google Scholar 

  31. He, Y.: A fully discrete stabilized finite-element method for the time-dependent Navier–Stokes problem. IMA J. Numer. Anal. 23, 665–691 (2003)

    MathSciNet  MATH  Google Scholar 

  32. He, W.-M., Guo, H.: Optimal maximum norm estimates for virtual element methods. SIAM J. Numer. Anal. 60(3), Article 3 (2022)

  33. He, M., Sun, P.: Error analysis of mixed finite element method for Poisson–Nernst–Planck system. Numer. Methods Partial Differ. Equ. 33, 1924–1948 (2017)

    MathSciNet  MATH  Google Scholar 

  34. He, M., Sun, P.: Mixed finite element analysis for the Poisson–Nernst–Planck/Stokes coupling. J. Comput. Appl. Math. 341, 61–79 (2018)

    MathSciNet  MATH  Google Scholar 

  35. Heywood, J.G., Rannacher, R.: Finite element approximation of the nonstationary Navier–Stokes problem. I. Regularity of solutions and second-order error estimates for spatial discretization. SIAM J. Numer. Anal. 19, 275–311 (1982)

    MathSciNet  MATH  Google Scholar 

  36. Hu, Y., Lee, J.S., Werner, C., Li, D.: Electrokinetically controlled concentration gradients in micro-chambers in microfluidic systems. Microfluid. Nanofluid. 2(2), 141–153 (2005)

    Google Scholar 

  37. Jerome, J.W.: Analytical approaches to charge transport in a moving medium. Transp. Theory Stat. Phys. 31, 333–366 (2002)

    MathSciNet  MATH  Google Scholar 

  38. Jerome, J.W.: Consistency of semiconductor modeling: an existence/stability analysis for the stationary Van Boosbroeck system. SIAM J. Appl. Math. 45, 565–590 (1985)

    MathSciNet  MATH  Google Scholar 

  39. Jerome, J.W.: The steady boundary value problem for charged incompressible fluids: PNP/Navier–Stokes systems. Nonlinear Anal. 74, 7486–7498 (2011)

    MathSciNet  MATH  Google Scholar 

  40. Jerome, J.W., Chini, B., Longaretti, M., Sacco, R.: Computational modeling and simulation of complex systems in bio-electronics. J. Comput. Electron. 7(1), 10–13 (2008)

    Google Scholar 

  41. Karatay, E., Druzgalski, C.L., Mani, A.: Simulation of chaotic electrokinetic transport: performance of commercial software versus custom-built direct numerical simulation codes. J. Colloid Interface Sci. 446, 67–76 (2015)

    Google Scholar 

  42. Kim, S., Khanwalea, M.A., Anand, R.K., Ganapathysubramanian, B.: Computational framework for resolving boundary layers in electrochemical systems using weak imposition of Dirichlet boundary conditions. Finite Elem. Anal. Des. 205, e103749 (2022)

    MathSciNet  Google Scholar 

  43. Linga, G., Bolet, A., Mathiesen, J.: Transient electrohydrodynamic flow with concentration-dependent fluid properties: modelling and energy-stable numerical schemes. J. Comput. Phys. 412, e109430 (2020)

    MathSciNet  MATH  Google Scholar 

  44. Liu, X., Chen, Z.: The nonconforming virtual element method for the Navier–Stokes equations. Adv. Comput. Math. 45(1), 51–74 (2019)

    MathSciNet  MATH  Google Scholar 

  45. Liu, Y., Shu, S., Wei, H., Yang, Y.: A virtual element method for the steady-state Poisson–Nernst–Planck equations on polygonal meshes. Comput. Math. Appl. 102, 95–112 (2021)

    MathSciNet  MATH  Google Scholar 

  46. Lu, B., Holst, M., McCammon, J., Zhou, Y.: Poisson–Nernst–Planck equations for simulating biomolecular diffusion–reaction processes I: finite element solutions. J. Comput. Phys. 229, 6979–6994 (2010)

    MathSciNet  MATH  Google Scholar 

  47. Mauri, A., Bortolossi, A., Novielli, G., Sacco, R.: 3D finite element modeling and simulation of industrial semiconductor devices including impact ionization. J. Math. Ind. 5, e18 (2015)

    MathSciNet  Google Scholar 

  48. Nirenberg, L.: An extended interpolation inequality. Ann. Scuola Norm. Sup. Pisa 20(3), 733–737 (1966)

    MathSciNet  MATH  Google Scholar 

  49. Park, J.-H., Jerome, J.W.: Qualitative properties of steady-state Poisson–Nernst–Planck systems: mathematical study. SIAM J. Appl. Math. 57(3), 609–630 (1997)

    MathSciNet  MATH  Google Scholar 

  50. Prohl, A., Schmuck, M.: Convergent discretizations for the Nernst–Planck–Poisson system. Numer. Math. 111, 591–630 (2009)

    MathSciNet  MATH  Google Scholar 

  51. Prohl, A., Schmuck, M.: Convergent finite element discretizations of the Navier–Stokes–Nernst–Planck–Poisson system. ESAIM Math. Model. Numer. Anal. 44, 531–571 (2010)

    MathSciNet  MATH  Google Scholar 

  52. Ryham, R.J.: An energetic variational approach to mathematical modeling of charged fluids: charge phases, simulation and well posedness. Doctoral dissertation, The Pennsylvania State University (2006)

  53. Schmuck, M.: Analysis of the Navier–Stokes–Nernst–Planck–Poisson system. Math. Models Methods Appl. Sci. 19(6), 993–1015 (2009)

    MathSciNet  MATH  Google Scholar 

  54. Vacca, G., Beirão da Veiga, L.: Virtual element methods for parabolic problems on polygonal meshes. Numer. Methods Partial Differ. Equ. 31(6), 2110–2134 (2015)

    MathSciNet  MATH  Google Scholar 

  55. Verma, N., Kumar, S.: Virtual element approximations for non-stationary Navier–Stokes equations on polygonal meshes. J. Appl. Anal. Comput., in press (2022)

  56. Wang, C., Bao, J., Pan, W., Sun, X.: Modeling electrokinetics in ionic liquids. Electrophoresis 00, 1–13 (2017)

    Google Scholar 

  57. Wang, G., Wang, F., He, Y.: A divergence-free weak virtual element method for the Navier–Stokes equation on polygonal meshes. Adv. Comput. Math. 47, e83 (2021)

    MathSciNet  Google Scholar 

  58. Wei, H., Huang, X., Li, A.: Piecewise divergence-free nonconforming virtual elements for Stokes problem in any dimensions. SIAM J. Numer. Anal. 59(3), 1835–1856 (2021)

    MathSciNet  MATH  Google Scholar 

  59. Xu, P., Capito, M., Cath, T.Y.: Selective removal of arsenic and monovalent ions from brackish water reverse osmosis concentrate. J. Hazard. Mater. 260, 885–891 (2013)

    Google Scholar 

  60. Xie, D., Lu, B.: An effective finite element iterative solver for a Poisson–Nernst–Planck ion channel model with periodic boundary conditions. SIAM J. Sci. Comput. 42(6), B1490–B1516 (2020)

    MathSciNet  MATH  Google Scholar 

  61. Yang, Y., Liu, Y., Shu, S.: Error analysis of virtual element methods for the time-dependent Poisson–Nernst–Planck equations. ArXiv preprint (2022). Available from arXiv:2207.07231

Download references

Acknowledgements

The authors are very grateful to the anonymous reviewers for carefully reading this paper and for their comments and suggestions, which have improved the paper.

Funding

The research of the third author has been partially supported by the Monash Mathematics Research Fund S05802-3951284, by the Australian Research Council through the Future Fellowship Grant FT220100496 and Discovery Project Grant DP22010316, and by the Ministry of Science and Higher Education of the Russian Federation within the framework of state support for the creation and development of World-Class Research Centers Digital biodesign and personalized healthcare No. 075-15-2022-304.

Author information

Authors and Affiliations

  1. Department of Applied Mathematics, Faculty of Mathematics and Computer Sciences, Amirkabir University of Technology (Tehran Polytechnic), No. 424, Hafez Ave., Tehran, 15914, Iran

    Mehdi Dehghan & Zeinab Gharibi

  2. School of Mathematics, Monash University, 9 Rainforest Walk, Melbourne, VIC, 3800, Australia

    Ricardo Ruiz-Baier

  3. World-Class Research Center “Digital Biodesign and Personalized Healthcare”, Sechenov First Moscow State Medical University, Moscow, Russia

    Ricardo Ruiz-Baier

  4. Universidad Adventista de Chile, Casilla 7-D, Chillan, Chile

    Ricardo Ruiz-Baier

Authors
  1. Mehdi Dehghan
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Zeinab Gharibi
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Ricardo Ruiz-Baier
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Mehdi Dehghan.

Ethics declarations

Conflict of interest

The authors have not disclosed any competing interests.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Dehghan, M., Gharibi, Z. & Ruiz-Baier, R. Optimal Error Estimates of Coupled and Divergence-Free Virtual Element Methods for the Poisson–Nernst–Planck/Navier–Stokes Equations and Applications in Electrochemical Systems. J Sci Comput 94, 72 (2023). https://doi.org/10.1007/s10915-023-02126-4

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10915-023-02126-4

Keywords

Mathematics Subject Classification

Search

Navigation