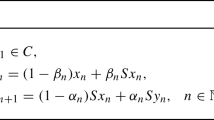Skip to main content
SpringerLink
Log in

Two Optimization Approaches for Solving Split Variational Inclusion Problems with Applications

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

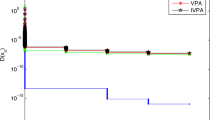
Using inertial effects, novel defined parameters and proximal-like algorithms with new variable stepsize rules, we propose two efficient optimization approaches for solving split variational inclusion problems in Hilbert spaces. Contrary with the work by Tang and Gibali (Numer Algorithms 83:305–331, 2020) and by Tan et al. (J Sci Comput 87:20, 2021), the proposed approaches do not require their stepsizes tending to zero and computing six values of the cost functions per iteration. These features can accelerate our methods. Weak and strong convergence of the introduced approaches are established without Lipschitz continuity of the cost functions and firm-nonexpansiveness of the proximal mappings. As applications, we mainly focus on the split feasibility and split minimization problems. Finally, several numerical experiments are provided for illustration and comparison.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

References

  1. Agarwal, R.P., Regan, D.O., Sahu, D.R.: Fixed Point Theory for Lipschitzian-Type Mappings with Applications. Topological Fixed Point Theory and Its Applications. Springer, New York, USA (2009)

    Google Scholar 

  2. Alvarez, F.: Weak convergence of a relaxed and inertial hybrid projection-proximal point algorithm for maximal monotone operators in Hilbert space. SIAM J. Optim. 14, 773–782 (2004)

    Article  MathSciNet  Google Scholar 

  3. Alvarez, F., Attouch, H.: An inertial proximal method for maximal monotone operators via discretization of a nonlinear oscillator with damping. Set-Valued Anal. 9, 3–11 (2001)

    Article  MathSciNet  Google Scholar 

  4. Aubin, J.P.: Optima and Equilibria: An Introduction to Nonlinear Analysis. Springer, Berlin (1993)

    Book  Google Scholar 

  5. Butnariu, D., Iusem, A.N.: Totally Convex Functions for Fixed Points Computation and Infinite Dimensional Optimization. Kluwer Academic Publishers, London (2000)

    Book  Google Scholar 

  6. Byrne, C.: Iterative oblique projection onto convex subsets and the split feasibility problem. Inverse Problems 16, 441–453 (2002)

    Article  Google Scholar 

  7. Byrne, C., Censor, Y., Gibali, A.: Weak and strong convergence of algorithms for the split common null point problem. J. Nonlinear Convex Anal 13, 759–775 (2011)

    MATH  Google Scholar 

  8. Censor, Y., Elfving, T.: A multiprojection algorithms using Bragman projection in a product space. Numer. Algorithms 8, 221–239 (1994)

    Article  MathSciNet  Google Scholar 

  9. Censor, Y., Elfving, T., Kopf, N., Bortfeld, T.: The multiple-sets split feasibility problem and its applications for inverse problems. Inv. Probl. 21, 2071–2084 (2005)

    Article  MathSciNet  Google Scholar 

  10. Censor, Y., Bortfeld, T., Martin, B., Trofmov, A.: A unifed approach for inversion problems in intensity-modulated radiation therapy. Phys. Med. Biol. 51, 2353–2365 (2006)

    Article  Google Scholar 

  11. Censor, Y., Gibali, A., Reich, S.: A von Neumann alternating method for finding common solutions to variational inequalities. Nonlinear Anal. 75, 4596–4603 (2012)

    Article  MathSciNet  Google Scholar 

  12. Censor, Y., Gibali, A., Reich, S., Sabach, S.: Common solutions to variational inequalities. Set Valued Var. Anal. 20, 229–247 (2012)

    Article  MathSciNet  Google Scholar 

  13. Censor, Y., Gibali, A., Reich, S.: Algorithms for the split variational inequality problem. Numer. Algorithm 59, 301–323 (2012)

    Article  MathSciNet  Google Scholar 

  14. Che, H., Li, M.: The conjugate gradient method for split variational inclusion and constrained convex minimization problems. Appl. Math. Comput. 290, 426–438 (2016)

    MathSciNet  MATH  Google Scholar 

  15. Chuang, C.S.: Algorithms with new parameter conditions for split variational inclusion problems in Hilbert spaces with application to split feasibility problem. Optimization 65, 859–876 (2016)

    Article  MathSciNet  Google Scholar 

  16. Chuang, C.S.: Hybrid inertial proximal algorithm for the split variational inclusion problem in Hilbert spaces with applications. Optimization 66, 777–792 (2017)

    Article  MathSciNet  Google Scholar 

  17. Combettes, P.L.: The convex feasibility problem in image recovery. In: Hawkes, P. (ed.) Advances in Imaging and Electron Physics, pp. 155–270. Academic Press, New York (1996)

    Google Scholar 

  18. Dang, Y.Z., Ang, M., Sun, J.: An inertial triple-projection algorithm for solving the split feasibility problem. J. Ind. Manag. Optim. (2022). https://doi.org/10.3934/jimo.2022019

  19. Gebrie, A.G., Bekele, B.: Viscosity self-adaptive method for generalized split system of variational inclusion problem. Bull. Iranian Math. Soc. (2020). https://doi.org/10.1007/s41980-020-00418-1

  20. He, H., Ling, C., Xu, H.K.: An implementable splitting algorithm for the \(\ell _{1}\)-norm regularized split feasibility problem. J. Sci. Comput. 67, 281–298 (2016)

    Article  MathSciNet  Google Scholar 

  21. Hieu, D.V.: Parallel extragradient-proximal methods for split equilibrium problems. Math. Model. Anal. 21, 478–501 (2016)

    Article  MathSciNet  Google Scholar 

  22. Hieu, D.V.: Two hybrid algorithms for solving split equilibrium problems. Int. J. Comput. Math. 95, 561–583 (2018)

    Article  MathSciNet  Google Scholar 

  23. Hieu, D.V.: Projection methods for solving split equilibrium problems. J. Ind. Manag. Optim. 16, 2331–2349 (2020)

    Article  MathSciNet  Google Scholar 

  24. Izuchukwu, C., Okeke, C.C., Isiogugu, F.O.: A viscosity iterative technique for split variational inclusion and fixed point problems between a Hilbert space and a Banach space. J. Fixed Point Theory Appl. 20, 157 (2018)

    Article  MathSciNet  Google Scholar 

  25. Kazmi, K.R., Rizvi, S.H.: An iterative method for split variational inclusion problem and fixed point problem for a nonexpansive mapping. Optim. Lett. 8, 1113–1124 (2014)

    Article  MathSciNet  Google Scholar 

  26. Kesornprom, S., Cholamjiak, P.: Proximal type algorithms involving linesearch and inertial technique for split variational inclusion problem in hilbert spaces with applications. Optimization (2019). https://doi.org/10.1080/02331934.2019.1638389

  27. Long, L.V., Thong, D.V., Dung, V.T.: New algorithms for the split variational inclusion problems and application to split feasibility problems. Optimization (2019). https://doi.org/10.1080/02331934.2019.1631821

  28. Maing\(\acute{e}\), P. E., Gobinddass, M. L.: Convergence of one-step projected gradient methods for variational inequalities. J. Optim. Theory Appl. 171, 146–168 (2016)

  29. Maing\(\acute{e}\), P.E.: Convergence theorems for inertial KM-type algorithms. J. Comput. Appl. Math. 219, 223–236 (2018)

  30. Majee, P., Nahak, C.: On inertial proximal algorithm for split variational inclusion problems. Optimization 67, 1701–1716 (2018)

    Article  MathSciNet  Google Scholar 

  31. Moudafi, A.: Split monotone variational inclusions. J. Optim. Theory Appl. 150, 275–283 (2011)

    Article  MathSciNet  Google Scholar 

  32. Nesterov, Y.: A method for solving the convex programming problem with convergence rate \(O(1/k^2)\). Dokl. Akad. Nauk SSSR 269, 543–547 (1983)

    MathSciNet  Google Scholar 

  33. Osilike, M.O., Aniagbosor, S.C.: Weak and strong convergence theorems for fixed points of asymptotically nonexpansive mappings. Math. Comput. Modell. 32, 1181–1191 (2000)

    Article  MathSciNet  Google Scholar 

  34. Polyak, B.T.: Some methods of speeding up the convergence of iteration methods. U. S. S. R. Comput. Math. Math. Phys. 4, 1–17 (1964)

    Article  Google Scholar 

  35. Sahu, D.R., Cho, Y.J., Dong, Q.L., Kashyap, M.R., Li, X.H.: Inertial relaxed CQ algorithms for solving a split feasibility problem in Hilbert spaces. Numer. Algorithms (2020). https://doi.org/10.1007/s11075-020-00999-2

  36. Shehu, Y., Gibali, A.: New inertial relaxed method for solving split feasibilities. Optim. Lett. 15, 2109–2126 (2021)

    Article  MathSciNet  Google Scholar 

  37. Shehu, Y., Iyiola, O.S.: Strong convergence result for proximal split feasibility problem in Hilbert spaces. Optimization 66, 2275–2290 (2017)

    Article  MathSciNet  Google Scholar 

  38. Sitthithakerngkiet, K., Deepho, J., Martinez-Moreno, J., Kuman, P.: Convergence analysis of a general iterative algorithm for finding a common solution of split variational inclusion and optimization problems. Numer. Algorithms 79, 801–824 (2018)

    Article  MathSciNet  Google Scholar 

  39. Taiwo, A., Alakoya, T.O., Mewomo, O.T.: Halpern-type iterative process for solving split common fixed point and monotone variational inclusion problem between Banach spaces. Numer. Algorithms (2020). https://doi.org/10.1007/s11075-020-00937-2

  40. Takahashi, W., Xu, H.K., Yao, J.C.: Iterative methods for generalized split feasibility problem in Hilbert spaces. Set Valued Var. Anal. 23, 205–221 (2015)

    Article  MathSciNet  Google Scholar 

  41. Tan, B., Qin, X., Yao, J.C.: Strong convergence of self-adaptive inertial algorithms for solving split variational inclusion problems with applications. J. Sci. Comput. 87, 20 (2021)

    Article  MathSciNet  Google Scholar 

  42. Tang, Y., Gibali, A.: New self-adaptive step size algorithms for solving split variational inclusion problems and its applications. Numer. Algorithms 83, 305–331 (2020)

    Article  MathSciNet  Google Scholar 

  43. Thong, D.V., Dung, V.T., Cho, Y.J.: A new strong convergence for solving split variational inclusion problems. Numer. Algorithms (2020). https://doi.org/10.1007/s11075-020-00901-0

  44. Tibshirani, R.: Regression shrinkage and selection via the Lasso. J. R. Stat. Soc. Ser. B 58, 267–288 (1996)

    MathSciNet  MATH  Google Scholar 

  45. Van Hieu, D., Reich, S., Anh, P.K., et al.: A new proximal-like algorithm for solving split variational inclusion problems. Numer. Algorithms (2021). https://doi.org/10.1007/s11075-021-01135-4

  46. Xu, H.K.: Iterative algorithm for nonlinear operators. J. London Math. Soc. 66, 240–256 (2002)

    Article  MathSciNet  Google Scholar 

Download references

Funding

The second author was supported by National Natural Science Foundation of China (Grant No. 11801430).

Author information

Authors and Affiliations

  1. Xidian University School of Mathematics and Statistics, Xi’an, 710126, Shaanxi, China

    Xiaojun Ma, Hongwei Liu & Xiaoyin Li

Authors
  1. Xiaojun Ma
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Hongwei Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Xiaoyin Li
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Xiaojun Ma.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ma, X., Liu, H. & Li, X. Two Optimization Approaches for Solving Split Variational Inclusion Problems with Applications. J Sci Comput 91, 58 (2022). https://doi.org/10.1007/s10915-022-01832-9

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10915-022-01832-9

Keywords

Mathematics Subject Classification

Search

Navigation