Skip to main content
SpringerLink
Log in

A Posteriori Error Estimates for Elliptic Eigenvalue Problems Using Auxiliary Subspace Techniques

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

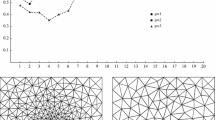
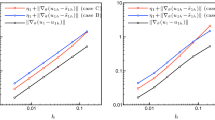
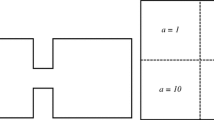
We propose an a posteriori error estimator for high-order p- or hp-finite element discretizations of selfadjoint linear elliptic eigenvalue problems that is appropriate for estimating the error in the approximation of an eigenvalue cluster and the corresponding invariant subspace. The estimator is based on the computation of approximate error functions in a space that complements the one in which the approximate eigenvectors were computed. These error functions are used to construct estimates of collective measures of error, such as the Hausdorff distance between the true and approximate clusters of eigenvalues, and the subspace gap between the corresponding true and approximate invariant subspaces. Numerical experiments demonstrate the practical effectivity of the approach.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

References

  1. Babuška, I., Suri, M.: On locking and robustness in the finite element method. SIAM J. Numer. Anal. 29(5), 1261–1293 (1992)

    Article  MathSciNet  Google Scholar 

  2. Bank, R.E., Grubišić, L., Ovall, J.S.: A framework for robust eigenvalue and eigenvector error estimation and ritz value convergence enhancement. Appl. Numer. Math. 66, 1–29 (2013). https://doi.org/10.1016/j.apnum.2012.11.004

    Article  MathSciNet  MATH  Google Scholar 

  3. Boffi, D., Gallistl, D., Gardini, F., Gastaldi, L.: Optimal convergence of adaptive FEM for eigenvalue clusters in mixed form. Math. Comp. 86(307), 2213–2237 (2017). https://doi.org/10.1090/mcom/3212

    Article  MathSciNet  MATH  Google Scholar 

  4. Cancés, E., Dusson, G., Maday, Y., Stamm, B., Vohralík, M.: Guaranteed a posteriori bounds for eigenvalues and eigenvectors: multiplicities and clusters. Math. Comput. (2020). https://doi.org/10.1090/mcom/3549

    Article  MathSciNet  MATH  Google Scholar 

  5. Friedrichs, K.: Spektraltheorie halbbeschränkter operatoren und anwendung auf die spektralzerlegung von differentialoperatoren. Math. Ann. 109(1), 465–487 (1934). https://doi.org/10.1007/BF01449150

    Article  MathSciNet  MATH  Google Scholar 

  6. Giani, S., Grubišić, L., Międlar, A., Ovall, J.S.: Robust error estimates for approximations of non-self-adjoint eigenvalue problems. Numer. Math. 133(3), 471–495 (2016). https://doi.org/10.1007/s00211-015-0752-3

    Article  MathSciNet  MATH  Google Scholar 

  7. Golub, G.H., Van Loan, C.F.: Matrix computations. In: Johns Hopkins Studies in the Mathematical Sciences, 4th edn. Johns Hopkins University Press, Baltimore, MD (2013)

    Google Scholar 

  8. Grisvard, P.: Elliptic problems in nonsmooth domains, monographs and studies in mathematics, vol. 24. Pitman (Advanced Publishing Program), Boston, MA (1985)

    MATH  Google Scholar 

  9. Grisvard, P.: Singularities in boundary value problems. In: Recherches en Mathématiques Appliquées [Research in Applied Mathematics], vol. 22. Masson, Paris (1992)

    Google Scholar 

  10. Grubišić, L.: A posteriori estimates for eigenvalue/vector approximations. PAMM 6(1), 59–62 (2006)

    Article  Google Scholar 

  11. Grubišić, L., Ovall, J.S.: On estimators for eigenvalue/eigenvector approximations. Math. Comp. 78, 739–770 (2009)

    Article  MathSciNet  Google Scholar 

  12. Hakula, H., Neilan, M., Ovall, J.S.: A posteriori estimates using auxiliary subspace techniques. J. Sci. Comput. 72(1), 97–127 (2017). https://doi.org/10.1007/s10915-016-0352-0

    Article  MathSciNet  MATH  Google Scholar 

  13. Hakula, H., Tuominen, T.: Mathematica implementation of the high order finite element method applied to eigenproblems. Computing 95(1), 277–301 (2013). https://doi.org/10.1007/s00607-012-0262-4

    Article  MathSciNet  Google Scholar 

  14. Higham, N.J.: Estimating the matrix \(p\)-norm. Numer. Math. 62(4), 539–555 (1992). https://doi.org/10.1007/BF01396242

    Article  MathSciNet  MATH  Google Scholar 

  15. Jakobson, D., Levitin, M., Nadirashvili, N., Polterovich, I.: Spectral problems with mixed dirichlet-neumann boundary conditions: isospectrality and beyond. J. Comput. Appl. Math. 194(1), 141–155 (2006). https://doi.org/10.1016/j.cam.2005.06.019

    Article  MathSciNet  MATH  Google Scholar 

  16. Kato, T.: Perturbation theory for linear operators. In: Classics in Mathematics. Springer-Verlag, Berlin (1995)

    Google Scholar 

  17. Knyazev, A., Jujunashvili, A., Argentati, M.: Angles between infinite dimensional subspaces with applications to the Rayleigh-Ritz and alternating projectors methods. J. Funct. Anal. 259(6), 1323–1345 (2010). https://doi.org/10.1016/j.jfa.2010.05.018

    Article  MathSciNet  MATH  Google Scholar 

  18. Knyazev, A.V., Argentati, M.E.: Rayleigh-Ritz majorization error bounds with applications to FEM. SIAM J. Matrix Anal. Appl. 31(3), 1521–1537 (2009). https://doi.org/10.1137/08072574X

    Article  MathSciNet  MATH  Google Scholar 

  19. Kozlov, V.A., Rossmann, J., Mazya, V.G.: Elliptic boundary value problems in domains with point singularities, Mathematical Surveys and Monographs, vol. 52. American Mathematical Society, Providence, RI (1997)

    Google Scholar 

  20. Kuttler, J.R., Sigillito, V.G.: Eigenvalues of the Laplacian in two dimensions. SIAM Rev. 26(2), 163–193 (1984)

    Article  MathSciNet  Google Scholar 

  21. Ovtchinnikov, E.: Cluster robust error estimates for the Rayleigh-Ritz approximation. II. Estimates for eigenvalues. Linear Algebra Appl. 415(1), 188–209 (2006)

    Article  MathSciNet  Google Scholar 

  22. Schwab, C.: \(p\)- and \(hp\)-finite element methods. In: Numerical Mathematics and Scientific Computation. The Clarendon Press, Oxford University Press, New York (1998)

    Google Scholar 

  23. Szabo, B., Babuska, I.: Finite Element Analysis. Wiley, Hoboken (1991)

    MATH  Google Scholar 

  24. Watson, G.N.: A treatise on the theory of Bessel functions. In: Cambridge Mathematical Library. Cambridge University Press, Cambridge (1995)

    Google Scholar 

  25. Wigley, N.M.: Asymptotic expansions at a corner of solutions of mixed boundary value problems. J. Math. Mech. 13, 549–576 (1964)

    MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Engineering, Durham University, South Road, Durham, DH1 3LE, United Kingdom

    Stefano Giani

  2. Department of Mathematics, University of Zagreb, Bijenička 30, 10000, Zagreb, Croatia

    Luka Grubišić

  3. Department of Mathematics and Systems Analysis, Aalto University, Espoo, Finland

    Harri Hakula

  4. Fariborz Maseeh Department of Mathematics and Statistics, Portland State University, 464R Fariborz Maseeh Hall, Portland, OR, 97201, USA

    Jeffrey S. Ovall

Authors
  1. Stefano Giani
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Luka Grubišić
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Harri Hakula
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Jeffrey S. Ovall
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jeffrey S. Ovall.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Grubišić: The work of this author was supported by Hrvatska Zaklada za Znanost (Croatian Science Foundation) under the grant IP-2019-04-6268 - Randomized low rank algorithms and applications to parameter dependent problems.

Hakula: The work of this author was supported by the (FP7/2007–2013) ERC grant agreement no 339380

Ovall: The work of this author was supported by the National Science Foundation under contract DMS-1522471.

All: The authors gratefully acknowledge the Mathematisches Forschungsinstitut Oberwolfach for hosting them through the Research-In-Pairs program on the topic “High-Order Finite Element Methods for Elliptic Eigenvalue Problems”

Supplementary Information

Below is the link to the electronic supplementary material.

Supplementary material 1 (pdf 40 KB)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Giani, S., Grubišić, L., Hakula, H. et al. A Posteriori Error Estimates for Elliptic Eigenvalue Problems Using Auxiliary Subspace Techniques. J Sci Comput 88, 55 (2021). https://doi.org/10.1007/s10915-021-01572-2

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10915-021-01572-2

Keywords

Mathematics Subject Classification

Search

Navigation