Skip to main content
SpringerLink
Log in

Locally Conservative Immersed Finite Element Method for Elliptic Interface Problems

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

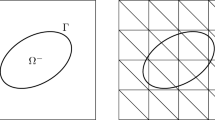
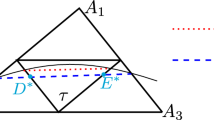
In this paper, we introduce a locally conservative enriched immersed finite element method (EIFEM) to tackle the elliptic problem with interface. The immersed finite element is useful for handling interface with mesh unfit with the interface. However, all the currently available method under IFEM framework may not be designed to consider the conservative flux conservation. We provide an efficient and effective remedy for this issue by introducing a local piecewise constant enrichment, which provides the locally conservative flux. We have also constructed and analyzed an auxiliary space preconditioner for the resulting system based on the application of algebraic multigrid method. The new observation in this work is that by imposing strong Dirichlet boundary condition for the standard IFEM part of EIFEM, we are able to remove the zero eigen-mode of the EIFEM system while still imposing the Dirichlet boundary condition weakly assigned to the piecewise constant enrichment part of EIFEM. A couple of issues relevant to the piecewise constant enrichment given for the mesh unfit to the interface has been discussed and clarified as well. Numerical tests are provided to confirm the theoretical development.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

References

  1. Arnold, D.N.: An interior penalty finite element method with discontinuous elements. SIAM J. Numer. Anal. 19, 742–760 (1982)

    MathSciNet  MATH  Google Scholar 

  2. Arnold, D.N., Brezzi, F., Cockburn, B., Marini, L.D.: Unified analysis of discontinuous Galerkin methods for elliptic problems. SIAM J. Numer. Anal. 39, 1749–1779 (2002)

    Article  MathSciNet  Google Scholar 

  3. Bastian, P., Rivière, B.: Superconvergence and \(h(div)\) projection for discontinuous Galerkin methods. Int. J. Numer. Methods Fluids 42, 1043–1057 (2003)

    Article  MathSciNet  Google Scholar 

  4. Belytschko, T., Black, T.: Elastic crack growth in finite elements with minimal remeshing. Int. J. Numer. Methods Eng. 45, 601–620 (1999)

    Article  Google Scholar 

  5. Belytschko, T., Parimi, C., Moës, N., Sukumar, N., Usui, S.: Structured extended finite element methods for solids defined by implicit surfaces. Int. J. Numer. Methods Eng. 56, 609–635 (2003)

    Article  Google Scholar 

  6. Bramble, J.H., King, J.T.: A finite element method for interface problems in domains with smooth boundaries and interfaces. Adv. Comput. Math. 6, 109–138 (1996)

    Article  MathSciNet  Google Scholar 

  7. Brezzi, F., Fortin, M.: Mixed and Hybrid Finite Element Methods, vol. 15. Springer, New York (1991)

    Book  Google Scholar 

  8. Chen, Z., Zou, J.: Finite element methods and their convergence for elliptic and parabolic interface problems. Numer. Math. 79, 175–202 (1998)

    Article  MathSciNet  Google Scholar 

  9. Chippada, S., Dawson, C., Martinez, M., Wheeler, M.: A projection method for constructing a mass conservative velocity field. Comput. Methods Appl. Mech. Eng. 157, 1–10 (1998)

    Article  MathSciNet  Google Scholar 

  10. Choi, Y., Jo, G., Kwak, D., Lee, Y.J.: Locally conservative discontinuous bubble scheme for darcy flow and its application to Hele–Shaw equation based on structured grids. Preprint (2021)

  11. Chou, S.H., Kwak, D.Y., Wee, K.T.: Optimal convergence analysis of an immersed interface finite element method. Adv. Comput. Math. 33, 149–168 (2010)

    Article  MathSciNet  Google Scholar 

  12. Cockburn, B., Gopalakrishnan, J., Wang, H.: Locally conservative fluxes for the continuous Galerkin method. SIAM J. Numer. Anal. 45, 1742–1776 (2007)

    Article  MathSciNet  Google Scholar 

  13. Demidov, D.: Amgcl: a c++ library for solution of large sparse linear systems with algebraic multigrid method (2017). https://github.com/ddemidov/amgcl

  14. Demidov, D.: Amgcl: an efficient, flexible, and extensible algebraic multigrid implementation. Lobachevskii J. Math. 40, 535–546 (2019)

    Article  MathSciNet  Google Scholar 

  15. Ern, S.N., Alexandre, Vohralík, M.: An accurate \(h(div)\) flux reconstruction for discontinuous Galerkin approximations of elliptic problems. C.R. Math. 345, 709–712 (2007)

    Article  MathSciNet  Google Scholar 

  16. Feng, W., He, X., Lin, Y., Zhang, X.: Immersed finite element method for interface problems with algebraic multigrid solver. Commun. Comput. Phys. 15, 1045–1067 (2014)

    Article  MathSciNet  Google Scholar 

  17. Guzmán, J., Sánchez, M.A., Sarkis, M.: Higher-order finite element methods for elliptic problems with interfaces. ESAIM Math. Model. Numer. Anal. 50, 1561–1583 (2016)

    Article  MathSciNet  Google Scholar 

  18. He, X., Lin, T., Lin, Y.: Approximation capability of a bilinear immersed finite element space. Numer. Methods Partial Differ. Equ. 24, 1265–1300 (2008)

    Article  MathSciNet  Google Scholar 

  19. Hiptmair, R., Xu, J.: Nodal auxiliary space preconditioning in h (curl) and h (div) spaces. SIAM J. Numer. Anal. 45, 2483–2509 (2007)

    Article  MathSciNet  Google Scholar 

  20. Hughes, T.J., Engel, G., Mazzei, L., Larson, M.G.: The continuous Galerkin method is locally conservative. J. Comput. Phys. 163, 467–488 (2000)

    Article  MathSciNet  Google Scholar 

  21. Jo, G., Kwak, D.Y.: A stabilized low order finite element method for three dimensional elasticity problems. Numerical Mathematics: Theory, Methods and Applications

  22. Jo, G., Kwak, D.Y.: An impes scheme for a two-phase flow in heterogeneous porous media using a structured grid. Computer Methods in Applied Mechanics and Engineering (2017)

  23. Jo, G., Kwak, D.Y.: Geometric multigrid algorithms for elliptic interface problems using structured grids. Numerical Algorithms (2018)

  24. Jo, G., Kwak, D.Y.: Recent development of immersed fem for elliptic and elastic interface problems. J. Korea Soc. Ind. Appl. Math. 23, 65–92 (2019)

    MathSciNet  MATH  Google Scholar 

  25. Krysl, P., Belytschko, T.: An efficient linear-precision partition of unity basis for unstructured meshless methods. Commun. Numer. Methods Eng. 16, 239–255 (2000)

    Article  MathSciNet  Google Scholar 

  26. Kwak, D.Y., Jin, S., Kyeong, D.: A stabilized \(p_1\)-nonconforming immersed finite element method for the interface elasticity problems. ESAIM Math. Model. Numer. Anal. 51, 187–207 (2017)

    Article  MathSciNet  Google Scholar 

  27. Kwak, D.Y., Wee, K.T., Chang, K.S.: An analysis of a broken \(p_1\)-nonconforming finite element method for interface problems. SIAM J. Numer. Anal. 48, 2117–2134 (2010)

    Article  MathSciNet  Google Scholar 

  28. Kwon, I., Kwak, D.Y.: Discontinuous bubble immersed finite element method for Poisson–Boltzmann equation. Commun. Comput. Phys. 25, 928–946 (2019)

    Article  MathSciNet  Google Scholar 

  29. Kyeong, D., Kwak, D.Y.: An immersed finite element method for the elasticity problems with displacement jump. Adv. Appl. Math. Mech. 9, 407–428 (2017)

    Article  MathSciNet  Google Scholar 

  30. Larson, M.G., Niklasson, A.J.: A conservative flux for the continuous Galerkin method based on discontinuous enrichment. Calcolo 41, 65–76 (2004)

    Article  MathSciNet  Google Scholar 

  31. Lee, S., Lee, Y., Wheeler, M.: A locally conservative enriched Galerkin approximation and user-friendly efficient solver for elliptic and parabolic problems. ICES report 15–19 (2015)

  32. Legrain, G., Moes, N., Verron, E.: Stress analysis around crack tips in finite strain problems using the extended finite element method. Int. J. Numer. Methods Eng. 63, 290–314 (2005)

    Article  MathSciNet  Google Scholar 

  33. Li, Z., Lin, T., Lin, Y., Rogers, R.C.: An immersed finite element space and its approximation capability. Numer. Methods Partial Differ. Equ. 20, 338–367 (2004)

    Article  MathSciNet  Google Scholar 

  34. Li, Z., Lin, T., Wu, X.: New Cartesian grid methods for interface problems using the finite element formulation. Numer. Math. 96, 61–98 (2003)

    Article  MathSciNet  Google Scholar 

  35. Lin, T., Lin, Y., Zhang, X.: Partially penalized immersed finite element methods for elliptic interface problems. SIAM J. Numer. Anal. 53, 1121–1144 (2015)

    Article  MathSciNet  Google Scholar 

  36. Moës, N., Dolbow, J., Belytschko, T.: A finite element method for crack growth without remeshing. Int. J. Numer. Methods Eng. 46, 131–150 (1999)

    Article  MathSciNet  Google Scholar 

  37. Nepomnyaschikh, S.: Decomposition and Fictitious Domains Methods for Elliptic Boundary Value Problems. Citeseer, Princeton (1991)

    MATH  Google Scholar 

  38. Raviart, P.A., Thomas, J.M.: A mixed finite element method for 2-nd order elliptic problems. Mathematical aspects of finite element methods, pp. 292–315 (1977)

  39. Rouitberg, J.A., et al.: A theorem on homeomorphisms for elliptic systems and its applications. Math. USSR Sbornik 7, 439 (1969)

    Article  Google Scholar 

  40. Sun, S., Liu, J.: A locally conservative finite element method based on piecewise constant enrichment of the continuous Galerkin method. SIAM J. Sci. Comput. 31, 2528–2548 (2009)

    Article  MathSciNet  Google Scholar 

  41. Wheeler, M.F.: An elliptic collocation-finite element method with interior penalties. SIAM J. Numer. Anal. 15, 152–161 (1978)

    Article  MathSciNet  Google Scholar 

  42. Xu, J.: The auxiliary space method and optimal multigrid preconditioning techniques for unstructured grids. Computing 56, 215–235 (1996)

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

First author is supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (No. 2020R1C1C1A01005396). Second author is supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (No. 2021R1A2C1003340). Third author is supported by Brain Pool Program through the National Research Foundation of Korea(NRF) funded by the Ministry of Science and ICT (Grant Number NRF-2020H1D3A2A01041079).

Author information

Authors and Affiliations

  1. Department of Mathematics, Kunsan National University, Kunsan, Republic of Korea

    Gwanghyun Jo

  2. Department of Mathematical Sciences, KAIST, Daejeon, Republic of Korea

    Do Y. Kwak

  3. Department of Mathematics, Texas State University, San Marcos, USA

    Young-Ju Lee

Authors
  1. Gwanghyun Jo
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Do Y. Kwak
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Young-Ju Lee
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Young-Ju Lee.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Jo, G., Kwak, D.Y. & Lee, YJ. Locally Conservative Immersed Finite Element Method for Elliptic Interface Problems. J Sci Comput 87, 60 (2021). https://doi.org/10.1007/s10915-021-01476-1

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10915-021-01476-1

Keywords

Search

Navigation