Skip to main content
SpringerLink
Log in

A Priori Neural Networks Versus A Posteriori MOOD Loop: A High Accurate 1D FV Scheme Testing Bed

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

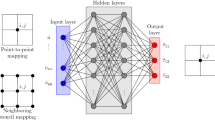
In this work we present an attempt to replace an a posteriori MOOD loop used in a high accurate Finite Volume (FV) scheme by a trained artificial Neural Network (NN). The MOOD loop, by decrementing the reconstruction polynomial degrees, ensures accuracy, essentially non-oscillatory, robustness properties and preserves physical features. Indeed it replaces the classical a priori limiting strategy by an a posteriori troubled cell detection, supplemented with a local time-step re-computation using a lower order FV scheme (ie lower polynomial degree reconstructions). We have trained shallow NNs made of only two so-called hidden layers and few perceptrons which a priori produces an educated guess (classification) of the appropriate polynomial degree to be used in a given cell knowing the physical and numerical states in its vicinity. We present a proof of concept in 1D. The strategy to train and use such NNs is described on several 1D toy models: scalar advection and Burgers’ equation, the isentropic Euler and radiative M1 systems. Each toy model brings new difficulties which are enlightened on the obtained numerical solutions. On these toy models, and for the proposed test cases, we observe that an artificial NN can be trained and substituted to the a posteriori MOOD loop in mimicking the numerical admissibility criteria and predicting the appropriate polynomial degree to be employed safely. The physical admissibility criteria is however still dealt with the a posteriori MOOD loop. Constructing a valid training data set is of paramount importance, but once available, the numerical scheme supplemented with NN produces promising results in this 1D setting.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23
Fig. 24
Fig. 25

Similar content being viewed by others

Notes

  1. We must be careful that the NN may be certain of its prediction, even if it is a wrong one.

  2. Notice that without the a posteriori MOOD loop the 2nd and 4th order schemes crash due to the occurrence of negative densities.

References

  1. Berg, J., Nyström, K.: A unified deep artificial neural network approach to partial differential equations in complex geometries. Neurocomputing 317, 28–41 (2018)

    Google Scholar 

  2. Blachère, F., Turpault, R.: An admissibility and asymptotic preserving scheme for systems of conservation laws with source term on 2d unstructured meshes with high-order mood reconstruction. Comput. Methods Appl. Mech. Eng. 317, 836–867 (2017)

    MathSciNet  MATH  Google Scholar 

  3. Blanchard, G., Loubère, R.: High order accurate conservative remapping scheme on polygonal meshes using a posteriori mood limiting. Comput. Fluids 136, 83–103 (2016)

    MathSciNet  MATH  Google Scholar 

  4. Boscheri, W., Dumbser, M., Loubère, R., Maire, P.-H.: A second-order cell-centered lagrangian ader-mood finite volume scheme on multidimensional unstructured meshes for hydrodynamics. J. Comput. Phys. 358, 103–129 (2018)

    MathSciNet  MATH  Google Scholar 

  5. Boscheri, W., Loubère, R., Dumbser, M.: Direct arbitrary-lagrangian-eulerian ader-mood finite volume schemes for multidimensional hyperbolic conservation laws. J. Comput. Phys. 292, 56–87 (2015)

    MathSciNet  MATH  Google Scholar 

  6. Braeunig, J.-P., Loubère, R., Motte, R., Peybernes, M., Poncet, R.: A posteriori limiting for 2d lagrange plus remap schemes solving the hydrodynamics system of equations. Comput. Fluids Recent Prog. Nonlinear Numer. Methods Time-dependent Flow Trans. Prob. 169, 249–262 (2018)

    MathSciNet  MATH  Google Scholar 

  7. Burgers, J.M.: The Nonlinear Diffusion Equation: Asymptotic Solutions and Statistical Problems. Springer, Berlin (1974)

    MATH  Google Scholar 

  8. Clain, S., Diot, S., Loubère, R.: A high-order finite volume method for systems of conservation laws–multi-dimensional optimal order detection (MOOD). J. Comput. Phys. 230(10), 4028–4050 (2011)

    MathSciNet  MATH  Google Scholar 

  9. Clain, S., Figueiredo, J.: The mood method for the non-conservative shallow-water system. Comput. Fluids 145, 99–128 (2017)

    MathSciNet  MATH  Google Scholar 

  10. Clain, S., Loubère, R., Machado, G.J.: A posteriori stabilized sixth-order finite volume scheme for one-dimensional steady-state hyperbolic equations. Adv. Comput. Math. 44(2), 571–607 (2018)

    MathSciNet  MATH  Google Scholar 

  11. Coudière, Y., Turpault, R.: A domain decomposition strategy for a very high-order finite volumes scheme applied to cardiac electrophysiology. J. Comput. Sci. 37, 101025 (2019)

    MathSciNet  Google Scholar 

  12. Diot, S., Clain, S., Loubère, R.: Improved detection criteria for the multi-dimensional optimal order detection (MOOD) on unstructured meshes with very high-order polynomials. Comput. Fluids 64(Supplement C), 43–63 (2012)

    MathSciNet  MATH  Google Scholar 

  13. Diot, S., Loubère, R., Clain, S.: The multidimensional optimal order detection method in the three-dimensional case: very high-order finite volume method for hyperbolic systems. Int. J. Numer. Meth. Fluids 73(4), 362–392 (2013)

    MathSciNet  Google Scholar 

  14. Dubroca, B., Feugeas, J.L.: Etude théorique et numérique d’une hiérarchie de modèles aux moments pour le transfert radiatif. Comptes Rendus l’Académie des Sci. Ser.I Math. 329(10), 915–920 (1999)

    MathSciNet  MATH  Google Scholar 

  15. Dumbser, M., Loubère, R.: A simple robust and accurate a posteriori sub-cell finite volume limiter for the discontinuous Galerkin method on unstructured meshes. J. Comput. Phys. 319(Supplement C), 163–199 (2016)

    MathSciNet  MATH  Google Scholar 

  16. Dumbser, M., Zanotti, O., Loubère, R., Diot, S.: A posteriori subcell limiting of the discontinuous galerkin finite element method for hyperbolic conservation laws. J. Comput. Phys. 278, 47–75 (2014)

    MathSciNet  MATH  Google Scholar 

  17. Fernández-Fidalgo, J., Nogueira, X., Ramírez, L., Colominas, I.: An a posteriori, efficient, high-spectral resolution hybrid finite-difference method for compressible flows. Comput. Methods Appl. Mech. Eng. 335, 91–127 (2018)

    MathSciNet  MATH  Google Scholar 

  18. Giri, P., Qiu, Q.J.J.: A high-order runge-kutta discontinuous galerkin method with a subcell limiter on adaptive unstructured grids for two-dimensional compressible inviscid flows. Int. J. Numer. Meth. Fluids 91(8), 367–394 (2019)

    MathSciNet  Google Scholar 

  19. Gottlieb, S., Shu, C.W.: Total variation diminishing Runge-Kutta schemes. Math. Comput. 67, 73–85 (1998)

    MathSciNet  MATH  Google Scholar 

  20. Gottlieb, S., Shu, C.-W.: Total variation diminishing Runge-Kutta schemes. Math. Comput. 6(221), 73–85 (1998)

    MathSciNet  MATH  Google Scholar 

  21. Gyrya, V., Shashkov, M., Skurikhin, A., Tokareva, S.: Machine learning approaches for the solution of the riemann problem in fluid dynamics: a case study. preprint, (2020)

  22. Hagan, M.T., Demuth, H.B., Beale, M.H.: Neural Network Design. PWS Publishing, India (1996)

    Google Scholar 

  23. Haykin, S.S.: Neural Networks and Learning Machines, 3rd edn. Pearson Education, London (2009)

    Google Scholar 

  24. Hebb, D.O.: The Organization of Behavior, vol. 65. Wiley, New York (1949)

    Google Scholar 

  25. Shu, C.-W., Qiu, J.: A comparison of troubled-cell indicators for Runge–Kutta discontinuous Galerkin methods using weighted essentially nonoscillatory limiters. J. Sci. Comput. 27, 995–1013 (2005)

    MathSciNet  MATH  Google Scholar 

  26. Jiang, G.-S., Shu, C.-W.: Efficient implementation of weighted eno schemes. J. Comput. Phys. 126(1), 202–228 (1996)

    MathSciNet  MATH  Google Scholar 

  27. Jiang, Z.-H., Yan, C., Jian, Y.: Efficient methods with higher order interpolation and mood strategy for compressible turbulence simulations. J. Comput. Phys. 371, 528–550 (2018)

    MathSciNet  MATH  Google Scholar 

  28. Kriesel, D.: A Brief Introduction to Neural Networks. (2007)

  29. Loubère, R., Dumbser, M., Diot, S.: A new family of high order unstructured MOOD and ADER finite volume schemes for multidimensional systems of hyperbolic conservation laws. Commun. Comput. Phys. 16(3), 718–763 (2014)

    MathSciNet  MATH  Google Scholar 

  30. Marquardt, D.: An algorithm for least-squares estimation of nonlinear parameters. SIAM J. Appl. Math. 11(2), 431–441 (1963)

    MathSciNet  MATH  Google Scholar 

  31. McCulloch, W.S., Pitts, W.: A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 5, 115–133 (1943)

    MathSciNet  MATH  Google Scholar 

  32. Minsky, M., Papert, S.: Perceptrons: An Introduction to Computational Geometry. MIT Press, Cambridge (1969)

    MATH  Google Scholar 

  33. Nogueira, X., Ramírez, L., Clain, S., Loubère, R., Cueto-Felgueroso, L., Colominas, I.: High-accurate sph method with multidimensional optimal order detection limiting. Comput. Methods Appl. Mech. Eng. 310, 134–155 (2016)

    MathSciNet  MATH  Google Scholar 

  34. Maziar Raissi and George Em Karniadakis: Hidden physics models: machine learning of nonlinear partial differential equations. J. Comput. Phys. 357, 125–141 (2018)

    MathSciNet  MATH  Google Scholar 

  35. Ray, D., Hesthaven, J.S.: An artificial neural network as a troubled-cell indicator. J. Comput. Phys. 367, 166–191 (2018)

    MathSciNet  MATH  Google Scholar 

  36. Ray, D., Hesthaven, J.S.: Detecting troubled-cells on two-dimensional unstructured grids using a neural network. J. Comput. Phys. 397, 108845 (2019)

    MathSciNet  Google Scholar 

  37. Rosenblatt, F.: The perceptron: a probabilistic model for information storage and organization in the brain. Psychological Review, pp. 65–386, (1958)

  38. Rosenblatt, F.: Principles of Neurodynamics. Spartan, New York (1962)

    MATH  Google Scholar 

  39. Sarazin-Desbois, C.: Méthodes numériques pour des systèmes hyperboliques avec terme source provenant de physiques complexes autour du rayonnement. Ph.D. thesis, Université de Nantes, (2013)

  40. Schmidhuber, J.: Deep learning in neural networks: an overview. Neural Networks 61, 85–117 (2015)

    Google Scholar 

  41. Semplice, M., Loubère, R.: Adaptive-mesh-refinement for hyperbolic systems of conservation laws based on a posteriori stabilized high order polynomial reconstructions. J. Comput. Phys. 354, 86–110 (2018)

    MathSciNet  MATH  Google Scholar 

  42. Suresh, A., Huynh, H.T.: Accurate monotonicity-preserving schemes with runge-kutta time stepping. J. Comput. Phys. 136, 83–99 (1997)

    MathSciNet  MATH  Google Scholar 

  43. Tann, S., Deng, X., Shimizu, Y., Loubère, R., Xiao, F.: Solution property preserving reconstruction for finite volume scheme: a bvd+mood framework. International Journal for Numerical Methods in Fluids, n/a(n/a), (2019)

  44. Toro, E.F.: Riemann Sovlers and Numerical Methods for Fluid Dynamics. Springer, Berlin (2009)

    Google Scholar 

  45. Veiga, M.H., Abgrall, R.: Towards a general stabilisation method for conservation laws using a multilayer perceptron neural network: 1d scalar and system of equations. In European Conference on Computational Mechanics and VII European Conference on Computational Fluid Dynamics, No. 1, pp. 2525–2550. ECCM, (June 2018)

  46. Vilar, F.: A posteriori correction of high-order discontinuous galerkin scheme through subcell finite volume formulation and flux reconstruction. J. Comput. Phys. 387, 245–279 (2019)

    MathSciNet  Google Scholar 

  47. Werbos, P.J.: Beyond Regression: New Tools for Prediction and Analysis in the Behavioral Sciences. Harvard University, Cambridge (1975)

    Google Scholar 

Download references

Acknowledgements

RL would like to thank M. Han Veiga (University of Zürich) and S. Clain (Universidade do Minho) for sharing fruitful discussions on neural networks. The authors thank the anonymous reviewers who have led to an improved version of this paper. The datasets generated during and/or analysed during the current study are available from the corresponding author on reasonable request.

Author information

Authors and Affiliations

  1. Institut de Mathématiques de Bordeaux (IMB), CNRS, Bordeaux INP, Université de Bordeaux, 33400, Talence, France

    Alexandre Bourriaud, Raphaël Loubère & Rodolphe Turpault

Authors
  1. Alexandre Bourriaud
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Raphaël Loubère
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Rodolphe Turpault
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Raphaël Loubère.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Bourriaud, A., Loubère, R. & Turpault, R. A Priori Neural Networks Versus A Posteriori MOOD Loop: A High Accurate 1D FV Scheme Testing Bed. J Sci Comput 84, 31 (2020). https://doi.org/10.1007/s10915-020-01282-1

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10915-020-01282-1

Keywords

Mathematics Subject Classification

Search

Navigation