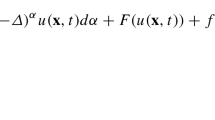Skip to main content
SpringerLink
Log in

Semi-implicit Galerkin–Legendre Spectral Schemes for Nonlinear Time-Space Fractional Diffusion–Reaction Equations with Smooth and Nonsmooth Solutions

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

For the first time in literature, semi-implicit spectral approximations for nonlinear Caputo time- and Riesz space-fractional diffusion equations with both smooth and non-smooth solutions are proposed. More precisely, the governing partial differential equation generalizes the Hodgkin–Huxley, the Allen–Cahn and the Fisher–Kolmogorov–Petrovskii–Piscounov equations. The schemes employ a Legendre-based Galerkin spectral method for the Riesz space-fractional derivative, and L1-type approximations with both uniform and graded meshes for the Caputo time-fractional derivative. More importantly, by using fractional Gronwall inequalities and their associated discrete forms, sharp error estimates are proved which show an enhancement in the convergence rate compared with the standard L1 approximation on uniform meshes. This analysis encompasses both uniform meshes as well as meshes that are graded in time, and guarantees the unconditional stability. The numerical results that accompany our analysis confirm our theoretical error estimates, and give significant insights into the convergence behavior of our schemes for problems with smooth and non-smooth solutions.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Podlubny, I.: Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications, vol. 198. Elsevier, Amsterdem (1998)

    MATH  Google Scholar 

  2. Li, X., Xu, C.: Existence and uniqueness of the weak solution of the space-time fractional diffusion equation and a spectral method approximation. Commun. Comput. Phys. 8(5), 1016–1051 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  3. Warma, M.: Approximate controllability from the exterior of space-time fractional diffusive equations. SIAM J. Control Optim. 57(3), 2037–2063 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  4. Liao, Hl, Li, D., Zhang, J.: Sharp error estimate of the nonuniform L1 formula for linear reaction-subdiffusion equations. SIAM J. Numeri. Anal. 56(2), 1112–1133 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  5. Lin, Y., Xu, C.: Finite difference/spectral approximations for the time-fractional diffusion equation. J. comput. phys. 225(2), 1533–1552 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  6. Alikhanov, A.A.: A new difference scheme for the time fractional diffusion equation. J. Comput. Phys. 280, 424–438 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  7. Chen, H., Stynes, M.: Error analysis of a second-order method on fitted meshes for a time-fractional diffusion problem. J. Sci. Comput. 79(1), 624–647 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  8. Lubich, C.: Convolution quadrature revisited. BIT Numer. Math. 44(3), 503–514 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  9. Jin, B., Lazarov, R., Zhou, Z.: Numerical methods for time-fractional evolution equations with nonsmooth data: a concise overview. Comput. Methods Appl. Mech. Eng. 346, 332–358 (2019)

    Article  MathSciNet  Google Scholar 

  10. Dehghan, M., Abbaszadeh, M.: An efficient technique based on finite difference/finite element method for solution of two-dimensional space/multi-time fractional Bloch–Torrey equations. Appl. Numer. Math. 131, 190–206 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  11. Stynes, M.: Too much regularity may force too much uniqueness. Fract. Calc. Appl. Anal. 19(6), 1554–1562 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  12. Liao, H.l., McLean, W., Zhang, J.: A second-order scheme with nonuniform time steps for a linear reaction–sudiffusion problem. arXiv preprint arXiv:1803.09873 (2018)

  13. Stynes, M., O’Riordan, E., Gracia, J.L.: Error analysis of a finite difference method on graded meshes for a time-fractional diffusion equation. SIAM J. Numer. Anal. 55(2), 1057–1079 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  14. Zeng, F., Zhang, Z., Karniadakis, G.E.: Second-order numerical methods for multi-term fractional differential equations: smooth and non-smooth solutions. Comput. Methods Appl. Mech. Eng. 327, 478–502 (2017)

    Article  MathSciNet  Google Scholar 

  15. Cao, W., Zeng, F., Zhang, Z., Karniadakis, G.E.: Implicit-explicit difference schemes for nonlinear fractional differential equations with nonsmooth solutions. SIAM J. Sci. Comput. 38(5), A3070–A3093 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  16. Samiee, M., Zayernouri, M., Meerschaert, M.M.: A unified spectral method for FPDEswith two-sided derivatives; part ii: Stability, and error analysis. J. Comput. Phys. 385, 244–261 (2019)

    Article  MathSciNet  Google Scholar 

  17. Bhrawy, A.H., Zaky, M.A.: A method based on the Jacobi tau approximation for solving multi-term time-space fractional partial differential equations. J. Comput. Phys. 281, 876–895 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  18. Zaky, M.A.: Recovery of high order accuracy in Jacobi spectral collocation methods for fractional terminal value problems with non-smooth solutions. J. Comput. Appl. Math. 357, 103–122 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  19. Shen, Jy, Sun, Zz, Du, R.: Fast finite difference schemes for time-fractional diffusion equations with a weak singularity at initial time. East Asian J. Appl. Math. 8(4), 834–858 (2018)

    Article  MathSciNet  Google Scholar 

  20. Zhang, J., Chen, H., Lin, S., Wang, J.: Finite difference/spectral approximation for a time-space fractional equation on two and three space dimensions. Comput. Math. Appl. 78, 1937–1946 (2019)

    Article  MathSciNet  Google Scholar 

  21. Ran, M., Zhang, C.: Linearized Crank–Nicolson scheme for the nonlinear time-space fractional Schrödinger equations. J. Comput. Appl. Math. 355, 218–231 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  22. Li, D., Liao, H.L., Sun, W., Wang, J., Zhang, J.: Analysis of L1-Galerkin FEMs for time-fractional nonlinear parabolic problems. Commun. Comput. Phys 24(1), 86–103 (2018)

    Article  MathSciNet  Google Scholar 

  23. Li, L., Zhou, B., Chen, X., Wang, Z.: Convergence and stability of compact finite difference method for nonlinear time fractional reaction-diffusion equations with delay. Appl. Math. Comput. 337, 144–152 (2018)

    MathSciNet  MATH  Google Scholar 

  24. Liao, Hl, McLean, W., Zhang, J.: A discrete Grönwall inequality with applications to numerical schemes for subdiffusion problems. SIAM J. Numer. Anal. 57(1), 218–237 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  25. Hendy, A.S., Macías-Díaz, J., Serna-Reyes, A.J.: On the solution of hyperbolic two-dimensional fractional systems via discrete variational schemes of high order of accuracy. J. Comput. Appl. Math. 354(7), 612–622 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  26. Macías-Díaz, J.E., Hendy, A.S., De Staelen, R.H.: A compact fourth-order in space energy-preserving method for Riesz space-fractional nonlinear wave equations. Appl. Math. Comput. 325, 1–14 (2018)

    MathSciNet  MATH  Google Scholar 

  27. Ervin, V.J., Roop, J.P.: Variational solution of fractional advection dispersion equations on bounded domains in \({\mathbf{R}}^d\). Numer. Methods Part. Differ. Equ. 23(2), 256–281 (2007)

    Article  MATH  Google Scholar 

  28. Zeng, F., Liu, F., Li, C., Burrage, K., Turner, I., Anh, V.: A Crank-Nicolson ADI spectral method for a two-dimensional Riesz space fractional nonlinear reaction-diffusion equation. SIAM J. Numer. Anal. 52(6), 2599–2622 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  29. Shen, J.: Efficient spectral-Galerkin method I. direct solvers of second-and fourth-order equations using Legendre polynomials. SIAM J. Sci. Comput. 15(6), 1489–1505 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  30. Brunner, H.: The numerical solution of weakly singular Volterra integral equations by collocation on graded meshes. Math. Comput. 45(172), 417–437 (1985)

    Article  MathSciNet  MATH  Google Scholar 

  31. Brunner, H., Ling, L., Yamamoto, M.: Numerical simulations of 2D fractional subdiffusion problems. J. Comput. Phys. 229(18), 6613–6622 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  32. Mustapha, K.: An implicit finite-difference time-stepping method for a sub-diffusion equation, with spatial discretization by finite elements. IMA J. Numer. Anal. 31(2), 719–739 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  33. Mustapha, K., McLean, W.: Superconvergence of a discontinuous Galerkin method for fractional diffusion and wave equations. SIAM J. Numer. Anal. 51(1), 491–515 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  34. Mustapha, K., Abdallah, B., Furati, K.M.: A discontinuous Petrov-Galerkin method for time-fractional diffusion equations. SIAM J. Numer. Anal. 52(5), 2512–2529 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  35. Zhang, H., Jiang, X., Wang, C., Fan, W.: Galerkin–Legendre spectral schemes for nonlinear space fractional Schrödinger equation. Numer. Algorithms 79(1), 337–356 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  36. Shen, J., Tang, T., Wang, L.L.: Spectral Methods: Algorithms, Analysis and Applications, vol. 41. Springer, Berlin (2011)

    Book  MATH  Google Scholar 

  37. Alikhanov, A.A.: A priori estimates for solutions of boundary value problems for fractional-order equations. Differ. Equ. 46(5), 660–666 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  38. Kilbas, A., Anatolii, A., Srivastava, H.M., Trujillo, J.J.: Theory and Applications of Fractional Differential Equation. Elsevier Science Limited, Amsterdam (2006)

    Google Scholar 

  39. Cheng, B., Guo, Z., Wang, D.: Dissipativity of semilinear time fractional subdiffusion equations and numerical approximations. Appl. Math. Lett. 86, 276–283 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  40. Li, L., Zhou, B., Chen, X., Wang, Z.: Convergence and stability of compact finite difference method for nonlinear time fractional reaction-diffusion equations with delay. Appl. Math. Comput. 337, 144–152 (2018)

    MathSciNet  MATH  Google Scholar 

  41. Cuesta, E., Lubich, C., Palencia, C.: Convolution quadrature time discretization of fractional diffusion-wave equations. Math. Comput. 75(254), 673–96 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  42. Sakamoto, K., Yamamoto, M.: Initial value/boundary value problems for fractional diffusion-wave equations and applications to some inverse problems. J. Math. Anal. Appl. 382(1), 426–47 (2011)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The second author wishes to acknowledge the support of RFBR Grant 19-01-00019. Meanwhile, the corresponding author wishes to acknowledge the financial support from the National Council for Science and Technology of Mexico (CONACYT) through Grant A1-S-45928. The authors wish to thank the referees for their constructive comments and suggestions which improved the paper.

Author information

Author notes

  1. Ahmed S. Hendy

    Present address: Department of Computational Mathematics and Computer Science, Institute of Natural Sciences and Mathematics, Ural Federal University, 19 Mira St., Yekaterinburg, Russia, 620002

Authors and Affiliations

  1. Department of Applied Mathematics, National Research Centre, Dokki, Giza, 12622, Egypt

    Mahmoud A. Zaky

  2. Department of Mathematics, Faculty of Science, Benha University, Benha, 13511, Egypt

    Ahmed S. Hendy

  3. Departamento de Matemáticas y Física, Universidad Autónoma de Aguascalientes, 20131, Aguascalientes, Ags., Mexico

    Jorge E. Macías-Díaz

Authors
  1. Mahmoud A. Zaky
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ahmed S. Hendy
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Jorge E. Macías-Díaz
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jorge E. Macías-Díaz.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zaky, M.A., Hendy, A.S. & Macías-Díaz, J.E. Semi-implicit Galerkin–Legendre Spectral Schemes for Nonlinear Time-Space Fractional Diffusion–Reaction Equations with Smooth and Nonsmooth Solutions. J Sci Comput 82, 13 (2020). https://doi.org/10.1007/s10915-019-01117-8

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10915-019-01117-8

Keywords

Mathematics Subject Classification

Search

Navigation