Skip to main content
SpringerLink
Log in

Discontinuity-Detecting Method for a Four-Point Stencil and Its Application to Develop a Third-Order Hybrid-WENO Scheme

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

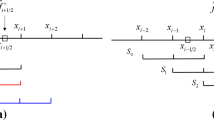
First this paper analyzes the reason for the accuracy losing of the third-order weighted essentially non-oscillatory (WENO) scheme. It is shown that one reason is that the local smoothness indicators of the third-order WENO scheme cannot correctly treat the smooth three-point stencil containing a non-nodal critical point, here, ‘non-nodal’ means the critical point is not a grid point. And then a discontinuity-detecting method for a four-point stencil is proposed and applied to develop the high order accurate hybrid-WENO scheme by combining the third-order WENO scheme and a third-order upstream scheme. This four-point stencil is actually the stencil used for constructing the third-order WENO scheme (positive and negative numerical fluxes), hence the resulting hybrid-WENO scheme proposed by this paper does not introduce new grid point. Numerical examples show that the detecting method and the hybrid scheme are robust for problems with shocks, and the hybrid scheme obtains real third-order convergence rate for smooth solutions containing critical points.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23
Fig. 24
Fig. 25
Fig. 26
Fig. 27

Similar content being viewed by others

References

  1. Liu, X.D., Osher, S., Chan, T.: Weighted essentially non-oscillatory schemes. J. Comput. Phys. 115, 200–212 (1994)

    Article  MathSciNet  Google Scholar 

  2. Harten, A., Engquist, B., Osher, S., Chakravarthy, S.: Uniformly high order essentially non-oscillatory schemes III. J. Comput. Phys. 71, 231–303 (1987)

    Article  MathSciNet  Google Scholar 

  3. Jiang, G.S., Shu, C.W.: Efficient implementation of weighted ENO schemes. J. Comput. Phys. 126, 202–228 (1996)

    Article  MathSciNet  Google Scholar 

  4. Balsara, D.S., Shu, C.W.: Monotonicity preserving weighted essentially non-oscillatory schemes with increasingly high order of accuracy. J. Comput. Phys. 160, 405–452 (2000)

    Article  MathSciNet  Google Scholar 

  5. Gerolymos, G., Senechal, D., Vallet, I.: Very-high-order WENO schemes. J. Comput. Phys. 228, 8481–8524 (2009)

    Article  MathSciNet  Google Scholar 

  6. Liu, S., Shen, Y., Chen, B., Zeng, F.: Novel local smoothness indicators for improving the third-order WENO scheme. Int. J. Numer. Methods Fluids 87, 51–69 (2018)

    Article  MathSciNet  Google Scholar 

  7. Yamaleev, N.K., Carpenter, M.H.: Third-order energy stable WENO scheme. J. Comput. Phys. 228, 3025–3047 (2009)

    Article  MathSciNet  Google Scholar 

  8. Wu, X., Zhao, Y.: A high-resolution hybrid scheme for hyperbolic conservation laws. Int. J. Numer. Methods Fluids 78, 162–187 (2015)

    Article  MathSciNet  Google Scholar 

  9. Wu, X., Lian, J., Zhao, Y.: A new smoothness indicator for third-order WENO scheme. Int. J. Numer. Methods Fluids 81, 451–459 (2016)

    Article  MathSciNet  Google Scholar 

  10. Gande, N.R., Rathod, Y., Rathan, S.: Third-order WENO scheme with a new smoothness indicator. Int. J. Numer. Methods Fluids 85, 90–112 (2017)

    Article  MathSciNet  Google Scholar 

  11. Xu, W., Wu, W.: An improved third-order weighted essentially non-oscillatory scheme achieving optimal order near critical points. Comput. Fluids 162, 113–125 (2018)

    Article  MathSciNet  Google Scholar 

  12. Xu, W., Wu, W.: An improved third-order WENO-Z scheme. J. Sci. Comput. 75, 1808–1841 (2018)

    Article  MathSciNet  Google Scholar 

  13. Acker, F., de Borges, R.B.R., Costa, B.: An improved WENO-Z scheme. J. Comput. Phys. 313, 726–753 (2016)

    Article  MathSciNet  Google Scholar 

  14. Henrick, A.K., Aslam, T.D., Powers, J.M.: Mapped weighted essentially non-oscillatory schemes: achieving optimal order near critical points. J. Comput. Phys. 207, 542–567 (2005)

    Article  Google Scholar 

  15. Shen, Y., Zha, G.: Generalized finite compact difference scheme for shock/complex flowfield interaction. J. Comput. Phys. 230, 4419–4436 (2011)

    Article  MathSciNet  Google Scholar 

  16. Shu, C.W., Osher, S.: Efficient implementation of essentially non-oscillatory shock-capturing schemes. J. Comput. Phys. 77, 439–471 (1988)

    Article  MathSciNet  Google Scholar 

  17. Szirtes, T., Rozsa, P.: Applied dimensional analysis and modeling (second edition). Appl. Dimens. Anal. Model. 25, 99–132 (2007)

    Article  Google Scholar 

  18. Najiafi-Yazdi, A., Mongeau, L.: A low-dispersion and low-dissipation implicit Runge–Kutta scheme. J. Comput. Phys. 233, 315–323 (2013)

    Article  MathSciNet  Google Scholar 

  19. Shu, C.W.: Essentially non-oscillatory and weighted essentially non-oscillatory schemes for hyperbolic conservation laws. ICASE Report 97–65 (1997)

  20. Borges, R., Carmona, M., Costa, B., Don, W.S.: An improved weighted essentially non-oscillatory scheme for hyperbolic conservation laws. J. Comput. Phys. 227, 3191–3211 (2008)

    Article  MathSciNet  Google Scholar 

  21. Roe, P.L.: Approximate Riemann solvers, parameter vectors, and difference schemes. J. Comput. Phys. 43, 357–372 (1981)

    Article  MathSciNet  Google Scholar 

  22. Sun, Y.Z., Wang, Z.: Evaluation of discontinuous Galerkin and spectral volume methods for scalar and system conservation laws on unstructured grids. Int. J. Numer. Methods Fluids 45, 819–838 (2004)

    Article  MathSciNet  Google Scholar 

  23. Davoudzadeh, F., McDonald, H., Thopson, B.: Accuracy evaluation of unsteady CFD numerical schemes by vortex preservation. Comput. Fluids 24, 883–895 (1995)

    Article  Google Scholar 

  24. Kurganov, A., Tadmor, E.: Solution of two-dimensional Riemann problems for gas dynamics without Riemann problem solvers. Numer. Methods Partial Differ. Equ. 18, 584–608 (2002)

    Article  MathSciNet  Google Scholar 

  25. Shen, Y.Q., Yang, G.W.: Hybrid finite compact-WENO schemes for shock calculation. Int. J. Numer. Methods Fluids 53, 531–560 (2007)

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

This research work was supported by the NKRDPC 2016YFA0401200, SCP No. TZ2016002, NSAF U1530145, NSFC Nos. 11872067 and 91852203.

Author information

Authors and Affiliations

  1. State Key Laboratory of High Temperature Gas Dynamics, Institute of Mechanics, Chinese Academy of Sciences, Beijing, 100190, China

    Shengping Liu & Yiqing Shen

  2. School of Aeronautic Science and Engineering, Beihang University, Beijing, 100191, China

    Shengping Liu

  3. School of Engineering Science, University of Chinese Academy of Sciences, Beijing, 100049, China

    Yiqing Shen

Authors
  1. Shengping Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yiqing Shen
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yiqing Shen.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

This research work was supported by the NKRDPC 2016YFA0401200, SCP No. TZ2016002, NSAF U1530145, NSFC Nos. 11872067 and 91852203.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Liu, S., Shen, Y. Discontinuity-Detecting Method for a Four-Point Stencil and Its Application to Develop a Third-Order Hybrid-WENO Scheme. J Sci Comput 81, 1732–1766 (2019). https://doi.org/10.1007/s10915-019-01060-8

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10915-019-01060-8

Keywords

Mathematics Subject Classification

Search

Navigation