Numerical Approximations for the Tempered Fractional Laplacian: Error Analysis and Applications

Abstract

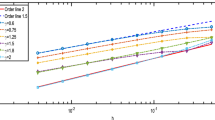
In this paper, we propose an accurate finite difference method to discretize the d-dimensional (for $d \ge 1$) tempered integral fractional Laplacian and apply it to study the tempered effects on the solution of problems arising in various applications. Compared to other existing methods, our method has higher accuracy and simpler implementation. Our numerical method has an accuracy of ${\mathcal {O}}(h^\varepsilon )$, for $u \in C^{0, \,\alpha + \varepsilon } (\bar{\Omega })$ if $\alpha < 1$ (or $u \in C^{1, \,\alpha - 1 + \varepsilon } (\bar{\Omega })$ if $\alpha \ge 1$) with $\varepsilon > 0$, suggesting the minimum consistency conditions. The accuracy can be improved to ${\mathcal {O}}(h^2)$, for $u \in C^{2, \,\alpha + \varepsilon } (\bar{\Omega })$ if $\alpha < 1$ (or $u \in C^{3, \,\alpha - 1 + \varepsilon } (\bar{\Omega })$ if $\alpha \ge 1$). Numerical experiments confirm our analytical results and provide insights in solving the tempered fractional Poisson problem. It suggests that to achieve the second order of accuracy, our method only requires the solution $u \in C^{1,1}(\bar{\Omega })$ for any $\alpha \in (0, 2)$. Moreover, if the solution of tempered fractional Poisson problems satisfies $u \in C^{p, s}(\bar{\Omega })$ for $p = 0, 1$ and $s\in (0, 1]$, our method has the accuracy of ${\mathcal {O}}(h^{p+s})$. Since our method yields a (multilevel) Toeplitz stiffness matrix, one can design fast algorithms via the fast Fourier transform for efficient simulations. Finally, we apply it together with fast algorithms to study the tempered effects on the solutions of various tempered fractional PDEs, including the Allen–Cahn equation and Gray–Scott equations.