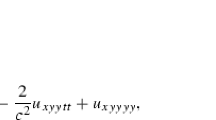Skip to main content
SpringerLink
Log in

Compact High Order Accurate Schemes for the Three Dimensional Wave Equation

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

We construct a family of compact fourth order accurate finite difference schemes for the three dimensional scalar wave (d’Alembert) equation with constant or variable propagation speed. High order accuracy is of key importance for the numerical simulation of waves as it reduces the dispersion error (i.e., the pollution effect). The schemes that we propose are built on a stencil that has only three nodes in any coordinate direction or in time, which eliminates the need for auxiliary initial or boundary conditions. These schemes are implicit in time and conditionally stable. A particular scheme with the maximum Courant number can be chosen within the proposed class. The inversion at the upper time level is done by FFT for constant coefficients and multigrid for variable coefficients, which keeps the overall complexity of time marching comparable to that of a typical explicit scheme.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

References

  1. Abide, S., Binous, M.S., Zeghmati, B.: An efficient parallel high-order compact scheme for the 3D incompressible Navier–Stokes equations. Int. J. Comput. Fluid Dyn. 31(4–5), 214–229 (2017). https://doi.org/10.1080/10618562.2017.1326592

    Article  MathSciNet  Google Scholar 

  2. Babuška, I.M., Sauter, S.A.: Is the pollution effect of the FEM avoidable for the Helmholtz equation considering high wave numbers? SIAM Rev. 42(3), 451–484 (electronic) (2000). Reprint of SIAM J. Numer. Anal. 34 (1997), no. 6, 2392–2423 [MR1480387 (99b:65135)]

  3. Bayliss, A., Goldstein, C.I., Turkel, E.: On accuracy conditions for the numerical computation of waves. J. Comput. Phys. 59(3), 396–404 (1985)

    Article  MathSciNet  Google Scholar 

  4. Bérenger, J.P.: Perfectly Matched Layer (PML) for Computational Electromagnetics. Synthesis Lectures on Computational Electromagnetics. Morgan and Claypool Publishers, San Rafael, CA (2007)

    Google Scholar 

  5. Brandt, A.: Rigorous quantitative analysis of multigrid. I. Constant coefficients two-level cycle with \(L_2\)-norm. SIAM J. Numer. Anal. 31(6), 1695–1730 (1994). https://doi.org/10.1137/0731087

    Article  MathSciNet  MATH  Google Scholar 

  6. Briggs, W.L., Henson, V.E., McCormick, S.F.: A Multigrid Tutorial, 2nd edn. Society for Industrial and Applied Mathematics (SIAM), Philadelphia (2000)

    Book  Google Scholar 

  7. Britt, S., Tsynkov, S., Turkel, E.: A compact fourth order scheme for the Helmholtz equation in polar coordinates. J. Sci. Comput. 45(1–3), 26–47 (2010). https://doi.org/10.1007/s10915-010-9348-3

    Article  MathSciNet  MATH  Google Scholar 

  8. Britt, S., Tsynkov, S., Turkel, E.: Numerical simulation of time-harmonic waves in inhomogeneous media using compact high order schemes. Commun. Comput. Phys. 9(3), 520–541 (2011)

    Article  MathSciNet  Google Scholar 

  9. Britt, S., Tsynkov, S., Turkel, E.: A high order compact time/space finite difference scheme for the wave equation with variable speed of sound. J. Sci. Comput. 76, 777–811 (2018). https://doi.org/10.1007/s10915-017-0639-9

    Article  MathSciNet  MATH  Google Scholar 

  10. Britt, S., Tsynkov, S., Turkel, E.: Numerical solution of the wave equation with variable wave speed on nonconforming domains by high-order difference potentials. J. Comput. Phys. 354, 26–42 (2018)

    Article  MathSciNet  Google Scholar 

  11. Chabassier, J., Imperiale, S.: Introduction and study of fourth order theta schemes for linear wave equations. J. Comput. Appl. Math. 245, 194–212 (2013). https://doi.org/10.1016/j.cam.2012.12.023

    Article  MathSciNet  MATH  Google Scholar 

  12. Deraemaeker, A., Babuška, I.M., Bouillard, P.: Dispersion and pollution of the FEM solution for the Helmholtz equation in one, two and three dimensions. Int. J. Numer. Methods Eng. 46, 471–499 (1999)

    Article  Google Scholar 

  13. Fishelov, D.: A new fourth-order compact scheme for the Navier–Stokes equations in irregular domains. Comput. Math. Appl. 74(1), 6–25 (2017). https://doi.org/10.1016/j.camwa.2016.10.020

    Article  MathSciNet  MATH  Google Scholar 

  14. Fu, Y.: Compact fourth-order finite difference schemes for Helmholtz equation with high wave numbers. J. Comput. Math. 26(1), 98–111 (2008)

    MathSciNet  MATH  Google Scholar 

  15. Grote, M.J., Sim, I.: Efficient PML for the wave equation (2010). arXiv:1001.0319

  16. Harari, I., Turkel, E.: Accurate finite difference methods for time-harmonic wave propagation. J. Comput. Phys. 119(2), 252–270 (1995)

    Article  MathSciNet  Google Scholar 

  17. Hocking, L.R., Greif, C.: Closed-form multigrid smoothing factors for lexicographic Gauss–Seidel. IMA J. Numer. Anal. 32(3), 795–812 (2012). https://doi.org/10.1093/imanum/drr037

    Article  MathSciNet  MATH  Google Scholar 

  18. Liang, H., Liu, M.Z., Lv, W.: Stability of \(\theta \)-schemes in the numerical solution of a partial differential equation with piecewise continuous arguments. Appl. Math. Lett. 23(2), 198–206 (2010). https://doi.org/10.1016/j.aml.2009.09.012

    Article  MathSciNet  MATH  Google Scholar 

  19. Lončarić, J., Tsynkov, S.V.: Optimization of acoustic source strength in the problems of active noise control. SIAM J. Appl. Math. 63(4), 1141–1183 (2003)

    Article  MathSciNet  Google Scholar 

  20. Ma, Y., Yu, J., Wang, Y.: An efficient complex-frequency shifted-perfectly matched layer for second-order acoustic wave equation. Int. J. Numer. Methods Eng. 97(2), 130–148 (2014). https://doi.org/10.1002/nme.4594

    Article  MathSciNet  MATH  Google Scholar 

  21. Ma, Y., Yu, J., Wang, Y.: A novel unsplit perfectly matched layer for the second-order acoustic wave equation. Ultrasonics 54(6), 1568–1574 (2014). https://doi.org/10.1016/j.ultras.2014.03.016

    Article  Google Scholar 

  22. Petropavlovsky, S., Tsynkov, S., Turkel, E.: A method of boundary equations for unsteady hyperbolic problems in 3D. J. Comput. Phys. 365, 294–323 (2018). https://doi.org/10.1016/j.jcp.2018.03.039

    Article  MathSciNet  MATH  Google Scholar 

  23. Ryaben’kii, V.S.: Method of Difference Potentials and Its Applications, Springer Series in Computational Mathematics, vol. 30. Springer, Berlin (2002)

    Book  Google Scholar 

  24. Saad, Y.: Iterative Methods for Sparse Linear Systems, 2nd edn. Society for Industrial and Applied Mathematics, Philadelphia (2003). https://doi.org/10.1137/1.9780898718003

    Book  MATH  Google Scholar 

  25. Singer, I., Turkel, E.: High-order finite difference methods for the Helmholtz equation. Comput. Methods Appl. Mech. Eng. 163(1–4), 343–358 (1998)

    Article  MathSciNet  Google Scholar 

  26. Singer, I., Turkel, E.: High-order finite difference methods for the Helmholtz equation. Comput. Methods Appl. Mech. Eng. 163(1–4), 343–358 (1998). https://doi.org/10.1016/S0045-7825(98)00023-1

    Article  MathSciNet  MATH  Google Scholar 

  27. Trottenberg, U., Oosterlee, C.W., Schüller, A.: Multigrid. Academic Press Inc., San Diego (2001). With contributions by A. Brandt, P. Oswald and K. Stüben

    MATH  Google Scholar 

  28. Turkel, E., Gordon, D., Gordon, R., Tsynkov, S.: Compact 2D and 3D sixth order schemes for the Helmholtz equation with variable wave number. J. Comput. Phys. 232(1), 272–287 (2013). https://doi.org/10.1016/j.jcp.2012.08.016

    Article  MathSciNet  MATH  Google Scholar 

  29. Zhou, L., Armfield, S.: A compact fourth-order spatial discretisation applied to the Navier–Stokes equations. ANZIAM Journal 56, 481–501 (2016)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, North Carolina State University, Box 8205, Raleigh, NC, 27695, USA

    F. Smith & S. Tsynkov

  2. School of Mathematical Sciences, Tel Aviv University, 69978, Ramat Aviv, Tel Aviv, Israel

    E. Turkel

Authors
  1. F. Smith
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. S. Tsynkov
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. E. Turkel
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to S. Tsynkov.

Additional information

We dedicate this paper to the memory of Professor Saul (Shalom) Abarbanel who provided mentorship and inspiration to a whole generation of students and colleagues.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Work supported by the US Army Research Office (ARO) under Grant No. W911NF-16-1-0115 and the US–Israel Binational Science Foundation (BSF) under Grant No. 2014048.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Smith, F., Tsynkov, S. & Turkel, E. Compact High Order Accurate Schemes for the Three Dimensional Wave Equation. J Sci Comput 81, 1181–1209 (2019). https://doi.org/10.1007/s10915-019-00970-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10915-019-00970-x

Keywords

Mathematics Subject Classification

Search

Navigation