Skip to main content
SpringerLink
Log in

Improvement of the Hydrostatic Reconstruction Scheme to Get Fully Discrete Entropy Inequalities

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

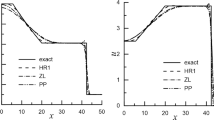
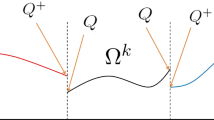
Abstract

This work is devoted to the derivation of an energy estimate to be satisfied by numerical schemes when approximating the weak solutions of the shallow water model. More precisely, here we adopt the well-known hydrostatic reconstruction technique to enforce the adopted Finite-Volume scheme to be well-balanced; namely to exactly preserve the lake at rest stationary solution. Such a numerical approach is known to get a semi-discrete (continuous in time) entropy inequality. However, a semi-discrete energy estimation turns, in general, to be insufficient to claim the required stability. In the present work, we adopt the artificial numerical viscosity technique to increase the desired stability and then to recover a fully discrete energy estimate. Several numerical experiments illustrate the relevance of the designed viscous hydrostatic reconstruction scheme.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

References

  1. Audusse, E., Bouchut, F., Bristeau, M.-O., Klein, R., Perthame, B.: A fast and stable well-balanced scheme with hydrostatic reconstruction for shallow water flows. SIAM J. Sci. Comput. 25(6), 2050–2065 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  2. Audusse, E., Bouchut, F., Bristeau, M.-O., Sainte-Marie, J.: Kinetic entropy inequality and hydrostatic reconstruction scheme for the saint-venant system. Math. Comput. 85(302), 2815–2837 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  3. Azerad, P., Guermond, J.-L., Popov, B.: Well-balanced second-order approximation of the shallow water equation with continuous finite elements. SIAM J. Numer. Anal. 55(6), 3203–3224 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  4. Bermudez, A., Vazquez, M.E.: Upwind methods for hyperbolic conservation laws with source terms. Comput. Fluids 23(8), 1049–1071 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  5. Berthon, C., Chalons, C.: A fully well-balanced, positive and entropy-satisfying godunov-type method for the shallow-water equations. Math. Comput. 85(299), 1281–1307 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  6. Berthon, C., Marche, F.: A positive preserving high order VFRoe scheme for shallow water equations: a class of relaxation schemes. SIAM J. Sci. Comput. 30(5), 2587–2612 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  7. F. Bouchut.: Nonlinear stability of finite volume methods for hyperbolic conservation laws and well-balanced schemes for sources. Frontiers in Mathematics. Birkhäuser Verlag, Basel (2004)

  8. Bouchut, F., de Luna, T.Morales: A subsonic-well-balanced reconstruction scheme for shallow water flows. SIAM J. Numer. Anal. 48(5), 1733–1758 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  9. Bouchut, F., de Luna, T.Morales: An entropy satisfying scheme for two-layer shallow water equations with uncoupled treatment. M2AN Math. Model. Numer. Anal. 42(4), 683–698 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  10. Cargo, P., Le Roux, A.-Y.: Un schéma équilibre adapté au modèle d’atmosphère avec termes de gravité. Comptes rendus de l’Académie des sciences. Série 1, Mathématique 318(1), 73–76 (1994)

  11. Chen, G., Noelle, S.: A new hydrostatic reconstruction scheme based on subcell reconstructions. SIAM J. Numer. Anal. 55(2), 758–784 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  12. Coquel, F., Saleh, K., Seguin, N.: A robust and entropy-satisfying numerical scheme for fluid flows in discontinuous nozzles. Math. Models Methods Appl. Sci. 24(10), 2043–2083 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  13. Couderc, F., Duran, A., Vila, J.-P.: An explicit asymptotic preserving low Froude scheme for the multilayer shallow water model with density stratification. J. Comput. Phys. 343, 235–270 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  14. Dafermos, C.M.: Hyperbolic conservation laws in continuum physics, volume 325 of Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences]. Springer-Verlag, Berlin, third edition, (2010)

  15. Delestre, O., Lagrée, P.-Y.: A ‘well-balanced’ finite volume scheme for blood flow simulation. Internat. J. Numer. Methods Fluids 72(2), 177–205 (2013)

    Article  MathSciNet  Google Scholar 

  16. Dubois, F., Mehlman, G.: A non-parameterized entropy correction for Roe’s approximate Riemann solver. Numer. Math. 73, 169–208 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  17. Fernández-Nieto, E.D., Garres-Díaz, J., Mangeney, A., Narbona-Reina, G.: 2D granular flows with the \(\mu (I)\) rheology and side walls friction: a well-balanced multilayer discretization. J. Comput. Phys. 356, 192–219 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  18. Gallouët, T., Hérard, J.-M., Seguin, N.: Some recent finite volume schemes to compute Euler equations using real gas EOS. Int. J. Numer. Methods Fluids 39(12), 1073–1138 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  19. Gallouët, T., Hérard, J.-M., Seguin, N.: Some approximate Godunov schemes to compute shallow water equations with topography. Comput. Fluids 32(4), 479–513 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  20. Godlewski, E., Raviart, P.-A.: Hyperbolic systems of conservation laws, volume 3/4 of Mathématiques & Applications (Paris) [Mathematics and Applications]. Ellipses, Paris, (1991)

  21. Godlewski, E., Raviart, P.-A.: Numerical Approximation of Hyperbolic Systems of Conservation laws, Volume 118 of Applied Mathematical Sciences. Springer, New York (1996)

    Book  MATH  Google Scholar 

  22. Godunov, S.K.: A difference method for numerical calculation of discontinuous solutions of the equations of hydrodynamics. Mat. Sb. (N.S.) 47(89), 271–306 (1959)

    MathSciNet  MATH  Google Scholar 

  23. Gosse, L.: A well-balanced flux-vector splitting scheme designed for hyperbolic systems of conservation laws with source terms. Comput. Math. Appl. 39(9), 135–159 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  24. Goutal, N., Maurel, F.: Proceedings of the 2nd workshop on dam-break wave simulation. Electricité de France, Direction des études et recherches (1997)

  25. Goutal, N., Maurel, F.: Dam-break wave simulation. In: Proceedings of the First CADAM workshop, (1998)

  26. Greenberg, J.M., Leroux, A.-Y.: A well-balanced scheme for the numerical processing of source terms in hyperbolic equations. SIAM J. Numer. Anal. 33(1), 1–16 (1996)

    Article  MathSciNet  Google Scholar 

  27. Greenberg, J.M., Leroux, A.Y., Baraille, R., Noussair, A.: Analysis and approximation of conservation laws with source terms. SIAM J. Numer. Anal. 34(5), 1980–2007 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  28. Grenier, N., Vila, J.-P., Villedieu, P.: An accurate low-Mach scheme for a compressible two-fluid model applied to free-surface flows. J. Comput. Phys. 252, 1–19 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  29. Guermond, J.-L., Popov, B.: Viscous regularization of the euler equations and entropy principles. SIAM J. Appl. Math. 74, 284–305 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  30. Guermond, J.-L., Popov, B.: Invariant domains and second-order continuous finite element approximation for scalar conservation equations. SIAM J. Numer. Anal. 55, 3120–3146 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  31. Harten, A., Lax, P.D., Van Leer, B.: On upstream differencing and Godunov-type schemes for hyperbolic conservation laws. SIAM Rev. 25, 35–61 (1983)

    Article  MathSciNet  MATH  Google Scholar 

  32. Harten, A., Hyman, J.M.: A self-adjusting grid for the computation of weak solutions of hyperbolic conservation laws. J. Comput. Phys. 50, 235–269 (1983)

    Article  MathSciNet  MATH  Google Scholar 

  33. Helluy, P., Hérard, J.-M., Mathis, H., Müller, S.: A simple parameter-free entropy correction for approximate Riemann solvers. Comptes Rendus Mécanique 338(9), 493–498 (2010)

    Article  MATH  Google Scholar 

  34. Jin, S.: A steady-state capturing method for hyperbolic systems with geometrical source terms. ESAIM: Math. Model. Numer. Anal. 35(04), 631–645 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  35. Lax, P.D.: Shock waves and entropy. In: Contributions to nonlinear functional analysis (Proc. Sympos., Math. Res. Center, Univ. Wisconsin, Madison, Wis., 1971), pages 603–634. Academic Press, New York (1971)

  36. Lax, P.D.: Hyperbolic Systems of Conservation Laws and the Mathematical Theory of Shock Waves, vol. 11. SIAM, New Delhi (1973)

    Book  MATH  Google Scholar 

  37. Lax, P.D., Wendroff, B.: Systems of conservation laws. Comm. Pure Appl. Math. 13, 217–237 (1960)

    Article  MathSciNet  MATH  Google Scholar 

  38. LeVeque, R.J.: Finite Volume Methods for Hyperbolic Problems. Cambridge Texts in Applied Mathematics. Cambridge University Press, Cambridge (2002)

    Book  Google Scholar 

  39. Li, G., Xing, Y.: Well-balanced discontinuous Galerkin methods with hydrostatic reconstruction for the Euler equations with gravitation. J. Comput. Phys. 352, 445–462 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  40. Liang, Q., Marche, F.: Numerical resolution of well-balanced shallow water equations with complex source terms. Adv. Water Resour. 32(6), 873–884 (2009)

    Article  Google Scholar 

  41. Maire, P.H., Abgrall, R., Breil, J., Ovadia, J.: A cell-centered Lagrangian scheme for two-dimensional compressible flow problems. SIAM J. Sci. Comput. 29, 1781–1824 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  42. Masella, J.-M., Faille, I., Gallouët, T.: On a rough godunov scheme. Int. J. for Comput. Fluid Dyn. 12(2), 133–150 (1999)

    Article  MATH  Google Scholar 

  43. Michel-Dansac, V., Berthon, C., Clain, S., Foucher, F.: A well-balanced scheme for the shallow-water equations with topography. Comput. Math. Appl. 72(3), 568–593 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  44. Michel-Dansac, V., Berthon, C., Clain, S., Foucher, F.: A well-balanced scheme for the shallow-water equations with topography or manning friction. J. Comput. Phys. 335, 115–154 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  45. Morales, T., Castro Díaz, M.J., Parés, C.: Reliability of first order numerical schemes for solving shallow water system over abrupt topography. Appl. Math. Comput. 219(17), 9012–9032 (2013)

    MathSciNet  MATH  Google Scholar 

  46. von Neumann, J., Richtmyer, R.D.: A method for the numerical calculation of hydrodynamic shocks. J. Appl. Phys. 21, 232–237 (1950)

    Article  MathSciNet  MATH  Google Scholar 

  47. Noh, W.F.: Errors for calculations of strong shocks using an artificial viscosity and an artificial heat flux. J. Comput. Phys. 72, 78–120 (1987)

    Article  MATH  Google Scholar 

  48. Perthame, B., Simeoni, C.: A kinetic scheme for the Saint-Venant system with a source term. Calcolo 38(4), 201–231 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  49. Roe, P.L.: Approximate Riemann solvers, parameter vectors, and difference schemes. J. Comput. Phys. 43(2), 357–372 (1981)

    Article  MathSciNet  MATH  Google Scholar 

  50. Serre, D.: Systems of conservation laws. 1. Cambridge University Press, Cambridge, (1999). Hyperbolicity, entropies, shock waves, Translated from the 1996 French original by I. N. Sneddon

  51. Tadmor, E.: Numerical viscosity and the entropy condition for conservative difference schemes. Math. Comput. 43(168), 369–381 (1984)

    Article  MathSciNet  MATH  Google Scholar 

  52. Tadmor, E.: The numerical viscosity of entropy stable schemes for systems of conservation laws. I. Math. Comput. 49(179), 91–103 (1987)

    Article  MathSciNet  MATH  Google Scholar 

  53. Tadmor, E.: Entropy stable schemes. Handbook of Numerical Methods for Hyperbolic Problems: Basic and Fundamental Issues, edited by R. Abgrall and C.-W. Shu (North-Holland, Elsevier, Amsterdam, 2017), 17:467–493 (2016)

  54. Toro, E.F.: Riemann solvers and numerical methods for fluid dynamics, 3rd edn. Springer, Berlin (2009). A practical introduction

    Book  MATH  Google Scholar 

  55. Toro, E.F., Spruce, M., Speares, W.: Restoration of the contact surface in the HLL-Riemann solver. Shock Waves 4(1), 25–34 (1994)

    Article  MATH  Google Scholar 

  56. Xu, K., Martinelli, L., Jameson, A.: Gas-kinetic finite volume methods, flux-vector splitting and artificial diffusion. J. Comput. Phys. 120, 48–65 (1995)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

We would like to thank the “Fédération de Recherche Mathématiques des Pays de Loire” (FMPL) as well as the SHARK-FV Conference for helping to initiate this project.

Author information

Authors and Affiliations

  1. Laboratoire de Mathématiques Jean Leray, CNRS UMR 6629, Université de Nantes, 2 rue de la Houssinière, BP 92208, 44322, Nantes, France

    Christophe Berthon

  2. Institut Camille Jordan, CNRS UMR 5208, Université Claude Bernard Lyon 1 43 boulevard du 11 novembre 1918, 69622, Villeurbanne Cedex, France

    Arnaud Duran & Khaled Saleh

  3. Laboratoire de Mathématiques Jean Leray, CNRS UMR 6629, Ecole Centrale de Nantes, 1 rue de la Noë, 44300, Nantes, France

    Françoise Foucher

  4. LAMI, Institut Universitaire de Technologie, Université Nazi BONI, O1 BP 1091, Bobo-Dioulasso 01, Burkina Faso

    Jean De Dieu Zabsonré

Authors
  1. Christophe Berthon
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Arnaud Duran
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Françoise Foucher
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Khaled Saleh
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Jean De Dieu Zabsonré
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Arnaud Duran.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Berthon, C., Duran, A., Foucher, F. et al. Improvement of the Hydrostatic Reconstruction Scheme to Get Fully Discrete Entropy Inequalities. J Sci Comput 80, 924–956 (2019). https://doi.org/10.1007/s10915-019-00961-y

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10915-019-00961-y

Keywords

Mathematics Subject Classification

Search

Navigation