Skip to main content
SpringerLink
Log in

A Fourth-Order Kernel-Free Boundary Integral Method for the Modified Helmholtz Equation

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

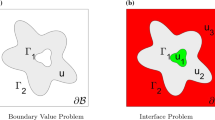
Based on the kernel-free boundary integral method proposed by Ying and Henriquez (J Comput Phys 227(2):1046–1074, 2007), which is a second-order accurate method for general elliptic partial differential equations, this work develops it to be a fourth-order accurate version for the modified Helmholtz equation. The updated method is in line with the original one. Unlike the traditional boundary integral method, it does not need to know any analytical expression of the fundamental solution or Green’s function in evaluation of boundary or volume integrals. Boundary value problems under consideration are reformulated into Fredholm boundary integral equations of the second kind, whose corresponding discrete forms are solved with the simplest Krylov subspace iterative method, the Richardson iteration. During each iteration, a Cartesian grid based nine-point compact difference scheme is used to discretize the simple interface problem whose solution is the boundary or volume integral in the BIEs. The resulting linear system is solved by a fast Fourier transform based solver, whose computational work is roughly proportional to the number of grid nodes in the Cartesian grid used. As the discrete boundary integral equations are well-conditioned, the iteration converges within an essentially fixed number of steps, independent of the mesh parameter. Numerical results are presented to verify the solution accuracy and demonstrate the algorithm efficiency.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

References

  1. Atkinson, K.E.: The Numerical Solution of Integral Equations of the Second Kind. Cambridge University Press, Cambridge (1997)

    Book  MATH  Google Scholar 

  2. Ben Avraham, D., Fokas, A.S.: The solution of the modified Helmholtz equation in a wedge and an application to diffusion-limited coalescence. Phys. Lett. A 263(4–6), 355–359 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  3. Bakker, M.: Modeling groundwater flow to elliptical lakes and through multi-aquifer elliptical inhomogeneities. Adv. Water Resour. 27(5), 497–506 (2004)

    Article  Google Scholar 

  4. Bakker, M., Kuhlman, K.L.: Computational issues and applications of line-elements to model subsurface flow governed by the modified Helmholtz equation. Adv. Water Resour. 34(9), 1186–1194 (2011)

    Article  Google Scholar 

  5. Banerjee, P.K., Butterfield, R.: Boundary Element Methods in Engineering Science, vol. 17. McGraw-Hill, London (1981)

    MATH  Google Scholar 

  6. Barnes, J., Hut, P.: A hierarchical O(N log N) force-calculation algorithm. Nature 324(6096), 446 (1986)

    Article  Google Scholar 

  7. Barnes, J.E.: A modified tree code: Don’t laugh. It runs. J. Comput. Phys. 87(1), 161–170 (1990)

    Article  MathSciNet  MATH  Google Scholar 

  8. Bazant, M.Z., Thornton, K., Ajdari, A.: Diffuse-charge dynamics in electrochemical systems. Phys. Rev. E 70(2), 021506 (2004)

    Article  Google Scholar 

  9. Beale, J.T., Layton, A.T.: On the accuracy of finite difference methods for elliptic problems with interfaces. Commun. Appl. Math. Comput. Sci. 1(1), 91–119 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  10. Brebbia, C., Dominguez, J.: Boundary element methods for potential problems. Appl. Math. Model. 1(7), 372–378 (1977)

    Article  MathSciNet  MATH  Google Scholar 

  11. Chapko, R., Kress, R.: Rothe’s method for the heat equation and boundary integral equations. J. Integral Equ. Appl. 9, 47–69 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  12. Cheng, H., Crutchfield, W.Y., Gimbutas, Z., Greengard, L.F., Ethridge, J.F., Huang, J., Rokhlin, V., Yarvin, N., Zhao, J.: A wideband fast multipole method for the Helmholtz equation in three dimensions. J. Comput. Phys. 216(1), 300–325 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  13. Cheng, H., Greengard, L., Rokhlin, V.: A fast adaptive multipole algorithm in three dimensions. J. Comput. Phys. 155(2), 468–498 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  14. Cheng, H., Huang, J., Leiterman, T.J.: An adaptive fast solver for the modified Helmholtz equation in two dimensions. J. Comput. Phys. 211(2), 616–637 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  15. Di Gioia, A.: Fast multipole accelerated boundary element techniques for large-scale problems, with applications to MEMS. Ph.D. thesis, Università di Trento. Dipartimento di ingegneria meccanica e strutturale (2005)

  16. Fedkiw, R.P., Aslam, T., Merriman, B., Osher, S.: A non-oscillatory eulerian approach to interfaces in multimaterial flows (the ghost fluid method). J. Comput. Phys. 152(2), 457–492 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  17. Feng, H., Barua, A., Li, S., Li, X.: A parallel adaptive treecode algorithm for evolution of elastically stressed solids. Commun. Comput. Phys. 15(2), 365–387 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  18. Gibou, F., Fedkiw, R., Cheng, L.T., Kang, M.: A second order accurate symmetric discretization of the Poisson equation on irregular domains. J. Comput. Phys. 176, 205–227 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  19. Gibou, F., Fedkiw, R.P.: A fourth order accurate discretization for the Laplace and heat equations on arbitrary domains, with applications to the Stefan problem. J. Comput. Phys. 202, 577–601 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  20. Greengard, L., Huang, J., Rokhlin, V., Wandzura, S.: Accelerating fast multipole methods for the Helmholtz equation at low frequencies. IEEE Comput. Sci. Eng. 5(3), 32–38 (1998)

    Article  Google Scholar 

  21. Greengard, L., Kropinski, M.C.: An integral equation approach to the incompressible Navier–Stokes equations in two dimensions. SIAM J. Sci. Comput. 20(1), 318–336 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  22. Greengard, L., Rokhlin, V.: A fast algorithm for particle simulations. J. Comput. Phys. 73(2), 325–348 (1987)

    Article  MathSciNet  MATH  Google Scholar 

  23. Greengard, L., Rokhlin, V.: A new version of the fast multipole method for the Laplace equation in three dimensions. Acta Numer. 6, 229–269 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  24. Hackbusch, W.: Integral Equations, Theory and Numerical Treatment. Birkhäuser, Basel (1995)

    Book  MATH  Google Scholar 

  25. Hackbusch, W., Nowak, Z.P.: On the fast matrix multiplication in the boundary element method by panel clustering. Numer. Math. 54(4), 463–491 (1989)

    Article  MathSciNet  MATH  Google Scholar 

  26. He, X., Lin, T., Lin, Y.: Immersed finite element methods for elliptic interface problems with non-homogeneous jump conditions. Int. J. Numer. Anal. Model. 8(2), 284–301 (2011)

    MathSciNet  MATH  Google Scholar 

  27. Hewett, D.W.: The embedded curved boundary method for orthogonal simulation meshes. J. Comput. Phys. 138(2), 585–616 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  28. Hou, S., Liu, X.D.: A numerical method for solving variable coefficient elliptic equation with interfaces. J. Comput. Phys. 202, 411–445 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  29. Houstis, E.N., Papatheodorou, T.S.: Algorithm 543: FFT9, fast solution of Helmholtz-type partial differential equations D3. ACM Trans. Math. Softw. 5(4), 490–493 (1979)

    Article  MATH  Google Scholar 

  30. Houstis, E.N., Papatheodorou, T.S.: High-order fast elliptic equation solver. ACM Trans. Math. Softw. 5(4), 431–441 (1979)

    Article  MATH  Google Scholar 

  31. Hsiao, G.C., Wendland, W.L.: Boundary Integral Equations. Springer, Berlin (2008)

    Book  MATH  Google Scholar 

  32. Jaswon, M.: Integral equation methods in potential theory. I. In: Proceedings of the Royal Society of London A, vol. 275, pp. 23–32. The Royal Society (1963)

  33. Johansen, H., Colella, P.: A Cartesian grid embedded boundary method for Poisson’s equation on irregular domains. J. Comput. Phys. 147(1), 60–85 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  34. Kropinski, M.C.A., Quaife, B.D.: Fast integral equation methods for Rothe’s method applied to the isotropic heat equation. Comput. Math. Appl. 61(9), 2436–2446 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  35. Kropinski, M.C.A., Quaife, B.D.: Fast integral equation methods for the modified Helmholtz equation. J. Comput. Phys. 230(2), 425–434 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  36. Kuhlman, K.L., Neuman, S.P.: Laplace-transform analytic-element method for transient porous-media flow. J. Eng. Math. 64(2), 113 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  37. Le, D.V., Khoo, B.C., Peraire, J.: An immersed interface method for viscous incompressible flows involving rigid and flexible boundaries. J. Comput. Phys. 220(1), 109–138 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  38. Leveque, R.J., Li, Z.: The immersed interface method for elliptic equations with discontinuous coefficients and singular sources. SIAM J. Numer. Anal. 31(4), 1019–1044 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  39. Li, H., Huang, J.: High accuracy solutions of the modified Helmholtz equation. In: Information Technology and Intelligent Transportation Systems, pp. 29–37. Springer (2017)

  40. Li, Z.: A fast iterative algorithm for elliptic interface problems. SIAM J. Numer. Anal. 35(1), 230–254 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  41. Li, Z., Ito, K.: The Immersed Interface Method: Numerical Solutions of PDEs Involving Interfaces and Irregular Domains, vol. 33. SIAM, Philadelphia (2006)

    Book  MATH  Google Scholar 

  42. Lindsay, K., Krasny, R.A.: A particle method and adaptive treecode for vortex sheet motion in three-dimensional flow. J. Comput. Phys. 172(2), 879–907 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  43. Liu, Y., Nishimura, N.: The fast multipole boundary element method for potential problems: a tutorial. Eng. Anal. Bound. Elem. 30(5), 371–381 (2006)

    Article  MATH  Google Scholar 

  44. Marques, A.N., Nave, J.C., Rosales, R.R.: A correction function method for Poisson problems with interface jump conditions. J. Comput. Phys. 230, 7567–7597 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  45. Marques, A.N., Nave, J.C., Rosales, R.R.: High order solution of Poisson problems with piecewise constant coefficients and interface jumps. J. Comput. Phys. 335, 497–515 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  46. Mayo, A.: The fast solution of Poisson’s and the biharmonic equations on irregular regions. SIAM J. Numer. Anal. 21(2), 285–299 (1984)

    Article  MathSciNet  MATH  Google Scholar 

  47. Mayo, A.: Fast high order accurate solution of Laplace’s equation on irregular regions. SIAM J. Sci. Stat. Comput. 6(1), 144–157 (1985)

    Article  MathSciNet  MATH  Google Scholar 

  48. Mayo, A.: The rapid evaluation of volume integrals of potential theory on general regions. J. Comput. Phys. 100(2), 236–245 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  49. Peskin, C.S.: The immersed boundary method. Acta Numer. 11, 479–517 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  50. Phillips, J.R., White, J.K.: A precorrected-FFT method for electrostatic analysis of complicated 3-D structures. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 16(10), 1059–1072 (1997)

    Article  Google Scholar 

  51. Politis, C.G., Papalexandris, M.V., Athanassoulis, G.A.: A boundary integral equation method for oblique water-wave scattering by cylinders governed by the modified helmholtz equation. Appl. Ocean Res. 24(4), 215–233 (2002)

    Article  Google Scholar 

  52. Quaife, B.D.: Fast integral equation methods for the modified Helmholtz equation. Ph.D. thesis, Science: Department of Mathematics (2011)

  53. Rokhlin, V.: Rapid solution of integral equations of classical potential theory. J. Comput. Phys. 60(2), 187–207 (1985)

    Article  MathSciNet  MATH  Google Scholar 

  54. Rosser, J.B.: Nine-point difference solutions for Poisson’s equation. Comput. Math. Appl. 1(3–4), 351–360 (1975)

    Article  MATH  Google Scholar 

  55. Saad, Y., Schultz, M.H.: GMRES: a generalized minimal residual algorithm for solving nonsymmetric linear systems. SIAM J. Sci. Stat. Comput. 7(3), 856–869 (1986)

    Article  MathSciNet  MATH  Google Scholar 

  56. Samarskii, A.A.: The Theory of Difference Schemes, vol. 240. CRC Press, London (2001)

    Book  MATH  Google Scholar 

  57. Sauter, S., Schwab, C.: Boundary Element Methods. Springer, Berlin (2010)

    Book  MATH  Google Scholar 

  58. Steinbach, O.: Numerical Approximation Methods for Elliptic Boundary Value Problems: Finite and Boundary Elements. Springer, Berlin (2007)

    Google Scholar 

  59. Strack, O.D.: Groundwater Mechanics. Prentice Hall, Englewood Cliffs (1989)

    Google Scholar 

  60. Ying, L., Biros, G., Zorin, D.: A kernel-independent adaptive fast multipole algorithm in two and three space dimensions. J. Comput. Phys. 196, 591–626 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  61. Ying, L., Biros, G., Zorin, D.: A high-order 3D boundary integral equation solver for elliptic PDEs in smooth domains. J. Comput. Phys. 219, 247–275 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  62. Ying, W., Henriquez, C.S.: A kernel-free boundary integral method for elliptic boundary value problems. J. Comput. Phys. 227(2), 1046–1074 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  63. Ying, W., Wang, W.C.: A kernel-free boundary integral method for implicitly defined surfaces. J. Comput. Phys. 252, 606–624 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  64. Ying, W., Wang, W.C.: A kernel-free boundary integral method for variable coefficients elliptic PDEs. Commun. Comput. Phys. 15(4), 1108–1140 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  65. Zhou, Y.C., Zhao, S., Feig, M., Wei, G.W.: High order matched interface and boundary method for elliptic equations with discontinuous coefficients and singular sources. J. Comput. Phys. 213(1), 1–30 (2006)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Mathematical Sciences, Shanghai Jiao Tong University, Minhang, Shanghai, 200240, People’s Republic of China

    Yaning Xie

  2. School of Mathematical Sciences, MOE-LSC and Institute of Natural Sciences, Shanghai Jiao Tong University, Minhang, Shanghai, 200240, People’s Republic of China

    Wenjun Ying

Authors
  1. Yaning Xie
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Wenjun Ying
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Wenjun Ying.

Additional information

The original version of this article was revised: The errors in the equations, texts and references have been corrected.

Research of the second author was supported in part by the National Science Foundation of the USA under Grant DMS 0915023, and is supported by the National Natural Science Foundation of China under Grants DMS 91330203, DMS 11101278, DMS 91130012 and DMS 11771290. Research of the second author was also supported by the Young Thousand Talents Program of China.

Appendix: Calculation for Jumps of Partial Derivatives

Appendix: Calculation for Jumps of Partial Derivatives

Jumps of partial derivatives of the solution to the interface problem (22) are needed not just in the correction for the finite difference equations but also in the extraction of boundary data from the discrete finite difference solutions.

Let \(u(\mathbf{x})\) be a piecewise smooth function defined in \({\mathcal B}\), whose normal derivative \(u_{\mathbf{n}}\) as well as u itself may be discontinuous across the interface. Computation of jumps for u on \(\varGamma \) starts from the interface problem (22), which is reiterated below

$$\begin{aligned} {\triangle }u -\kappa u= & {} \tilde{f} \quad \text {in }\,\, {\mathcal B}\setminus \varGamma , \end{aligned}$$
(40)
$$\begin{aligned}{}[u]= & {} \varphi \quad \text {on }\,\, \varGamma , \end{aligned}$$
(41)
$$\begin{aligned}{}[u_{\mathbf{n}}]= & {} \psi \quad \text {on }\,\, \varGamma . \end{aligned}$$
(42)

Let s be the arc length parameter of the curve \(\varGamma \), \(\mathbf{t} = (x'(s), y'(s))^\mathrm{T}\) be the unit tangent vector, \(\mathbf{n} = (y'(s), -x'(s))^\mathrm{T} = \mathbf{t}^{\perp }\) be the unit outward normal vector on \(\varGamma \). Suppose that \(\varphi = \varphi (s)\) and \(\psi = \psi (s)\) are two sufficiently smooth functions defined on \(\varGamma \).

Differentiating (41) with respect to the arc length parameter s, together with (42), we get

$$\begin{aligned} \left\{ \begin{array}{l} x'(s) [u_x] + y'(s) [u_y] = \varphi _s \\ y'(s) [u_x] - x'(s) [u_y] = \psi \end{array} \right. . \end{aligned}$$
(43)

Solving this two by two linear system gives us jumps of the first-order partial derivatives of u on \(\varGamma \).

Differentiating the identities in (43) with respect to the arc length parameter s, respectively, together with the modified Helmholtz equation (40), we get

$$\begin{aligned} \left\{ \begin{array}{l} (x')^2 [u_{xx}] + 2 x' y' [u_{xy}] + (y')^2 [u_{yy}] = \varphi _{ss} - \big \{ x''(s) [u_x] + y''(s) [u_y] \big \} \\ x' y' [u_{xx}] + \big \{ (y')^2 - (x')^2 \big \} [u_{xy}] - x'y' [u_{yy}] = \psi _s - y'' [u_x] + x'' [u_y] \\ {[} u_{xx} ] + [ u_{yy} ] = f +\kappa [u] \end{array} \right. . \end{aligned}$$
(44)

Solving this three by three linear system gives us jumps of the second-order partial derivatives of u on \(\varGamma \).

Differentiating the first equation in (44) with respect to the arc length parameter s gives us

$$\begin{aligned} (x')^3 [u_{xxx}] + 3 (x')^2 y' [u_{xxy}] + 3 x' (y')^2 [u_{xyy}] + (y')^3 [u_{yyy}] = r_{3,1} \end{aligned}$$
(45)

with

$$\begin{aligned} r_{3,1} = \varphi _{sss} - (x''' [u_x] + y''' [u_y]) - 3 \bigl \{ x''x' [u_{xx}] + (x'' y' + x' y'') [u_{xy}] + y'' y' [u_{yy}] \bigr \}. \end{aligned}$$

Differentiating the second equation in (44) with respect to the arc length parameter s gives us

$$\begin{aligned}&(x')^2 y' [u_{xxx}] + \bigl \{ 2 x' (y')^2 - (x')^3\bigr \} [u_{xxy}] \nonumber \\&\quad + \bigl \{ (y')^3 - 2 (x')^2 y' \bigr \} [u_{xyy}] - x' (y')^2 [u_{yyy}] = r_{3,2} \nonumber \\ \end{aligned}$$
(46)

with

$$\begin{aligned} r_{3,2}= & {} \psi _{ss} - y''' [u_x] + x''' [u_y] - (x''y' + 2 x' y'' ) [u_{xx}] \\&+ 3 ( x' x'' - y'y'') [u_{xy}] + (2 x'' y' + x' y'') [u_{yy}]. \end{aligned}$$

We may get two more equations for jumps of the third-order partial derivatives by first differentiating the modified Helmholtz equation and then taking jumps of the resulting equations across \(\varGamma \). They read

$$\begin{aligned} {[}u_{xxx}] + [u_{xyy}]= & {} f_x+\kappa \, [u_x], \end{aligned}$$
(47)
$$\begin{aligned} {[}u_{xxy}] + [u_{yyy}]= & {} f_y+\kappa \, [u_y]. \end{aligned}$$
(48)

We may get jumps of the third-order partial derivatives, \([u_{xxx}]\), \([u_{xxy}]\), \([u_{xyy}]\) and \([u_{yyy}]\), by solving the system consisting of Eqs. (45)–(48).

Differentiating (45) with respect to the arc length parameter s yields

$$\begin{aligned}&(x')^4 [u_{xxxx}] + 4 (x')^3 y' [u_{xxxy}] + 6 (x')^2 (y')^2 [u_{xxyy}] \nonumber \\&\quad +\,4 x' (y')^3 [u_{xyyy} + (y')^4 [u_{yyyy}] = r_{4,1} \nonumber \\ \end{aligned}$$
(49)

with

$$\begin{aligned} r_{4,1}= & {} \varphi _{ssss} - (x''''[u_x] + y''''[u_y]) -\bigl \{ (4 x'''x' + 3 x'' x'') [u_{xx}] \nonumber \\&+ \, (4 x''' y' + 6 x'' y'' + 4 x' y''') [u_{xy}] + (4 y''' y' + 3 (y'')^2) [u_{yy}] \bigr \}\nonumber \\&- \, 6 \bigl \{x''(x')^2 [u_{xxx}]+(2 x' x'' y' + (x')^2 y'') [u_{xxy}] \nonumber \\&+\, (x'' (y')^2 + 2 x' y' y'') [u_{xyy}]+ y'' (y')^2 [u_{yyy}] \bigr \} . \end{aligned}$$

Differentiating (46) with respect to the arc length parameter s leads to

$$\begin{aligned}&(x')^3 y' [u_{xxxx}]+(x')^2 \bigl \{3 (y')^2 - (x')^2 \bigr \} [u_{xxxy}]+ 3 x' y' \bigl \{(y')^2 - (x')^2 \bigr \} [u_{xxyy}] \nonumber \\&\quad + \, (y')^2 \bigl \{(y')^2 - 3 (x')^2 \bigr \} [u_{xyyy}] - x' (y')^3 [u_{yyyy}] = r_{4,2} \nonumber \\ \end{aligned}$$
(50)

with

$$\begin{aligned} r_{4,2}= & {} \psi _{sss} - y'''' [u_x] + x'''' [u_y] - (x'''y' + 3x''y'' + 3 x'y''' ) [u_{xx}] \\&+ \, ( 3 x'' x'' + 4 x' x''' - 3 y''y'' - 4 y' y''') [u_{xy}] + (3 x''' y' + 3 x'' y'' + x' y''') [u_{yy}] \\&- 3 \bigl \{ x' x'' y' + (x')^2 y'' \bigr \} [u_{xxx}] + 3 \bigl \{ 2 (x')^2 x'' - x'' (y')^2 - 3 x' y' y'' \bigr \} [u_{xxy}] \\&- 3 \bigl \{ 2 (y')^2 y'' - 3 x' x'' y' - (x')^2 y'' \bigr \} [u_{xyy}] + 3 \bigl \{ x'' (y')^2 + x' y' y'' \bigr \} [u_{yyy}]. \end{aligned}$$

Other three equations for jumps of the fourth-order partial derivatives read

$$\begin{aligned}{}[u_{xxxx}] + [u_{xxyy}]= & {} f_{xx}+\kappa [u_{xx}], \end{aligned}$$
(51)
$$\begin{aligned}{}[u_{xxxy}] + [u_{xyyy}]= & {} f_{xy}+\kappa [u_{xy}], \end{aligned}$$
(52)
$$\begin{aligned}{}[u_{xxyy}] + [u_{yyyy}]= & {} f_{yy}+\kappa [u_{yy}], \end{aligned}$$
(53)

which are similarly obtained by first differentiating the modified Helmholtz equation and then taking jumps of the resulting equations across \(\varGamma \).

We may get jumps of the fourth-order partial derivatives, \([u_{xxxx}]\), \([u_{xxxy}]\), \([u_{xxyy}]\), \([u_{xyyy}]\) and \([u_{yyyy}]\), by solving the system consisting of Eqs. (49)–(53).

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Xie, Y., Ying, W. A Fourth-Order Kernel-Free Boundary Integral Method for the Modified Helmholtz Equation. J Sci Comput 78, 1632–1658 (2019). https://doi.org/10.1007/s10915-018-0821-8

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10915-018-0821-8

Keywords

Search

Navigation