Hybrid Spectral Difference Methods for Elliptic Equations on Exterior Domains with the Discrete Radial Absorbing Boundary Condition

Abstract

The hybrid spectral difference methods (HSD) for the Laplace and Helmholtz equations in exterior domains are proposed. We consider the fictitious domain method with the absorbing boundary conditions (ABCs). The HSD method is a finite difference version of the hybridized Galerkin method, and it consists of two types of finite difference approximations; the cell finite difference and the interface finite difference. The fictitious domain is composed of two subregions; the Cartesian grid region and the boundary layer region in which the radial grid is imposed. The boundary layer region with the radial grid makes it easy to implement the discrete radial ABC. The discrete radial ABC is a discrete version of the Bayliss–Gunzburger–Turkel ABC without pertaining any radial derivatives. Numerical experiments confirming efficiency of our numerical scheme are provided.

1 Introduction

We consider the Laplace equation

$$\begin{aligned} \Delta u= & {} 0 \text { in } \Omega , \end{aligned}$$

and the Helmholtz equation

$$\begin{aligned} \Delta u +\omega ^2 u = 0 \text { in } \Omega \end{aligned}$$

(1.1)

on an exterior domain $\Omega$ with a Dirichlet boundary condition $u=g$ on $\partial \Omega$. For unique solvability of the above problems the decay conditions at infinity are required as follows:

$$\begin{aligned} \left\{ \begin{array}{l@{\quad }c@{\quad }c} u = O\left( \frac{1}{r}\right) , &{} r \rightarrow \infty , &{} \text {(Laplace)}\\ \frac{\partial u}{\partial r} - i\omega u =o\left( \frac{1}{r}\right) , &{} r \rightarrow \infty . &{} \text {(Helmholtz)} \end{array} \right. \end{aligned}$$

For the rest of the paper we regard the Laplace equation as a special case of the Helmholtz equation with $\omega =0$ for simplicity of notations.

As shown in Fig. 1 we consider a fictitious domain $\Omega _1 \cup \Omega _2$ with the inner boundary $\Gamma _1$ and outer boundary $\Gamma _2$ for the exterior domain problem. The outer boundary $\Gamma _2$ is a circle with radius $r_0 > 1$, and an absorbing boundary condition (ABC) is imposed on it, which replaces the decay condition at infinity. In $\Omega _1$ the Cartesian coordinate system is used, and the rectangular or trapezoidal partition is used for implementation of the hybrid difference method (see Fig. 3). The subdomain $\Omega _2$ is a thin layer boundary region with single or double layers, on which the polar coordinate system is used. The width of the boundary layer region is of size h, the maximum diameter of a partition of $\Omega _1$. Since our ABC is constructed based on the multipole expansion of a solution the layer boundary region with the polar coordinate and radial grid can be more efficient for implementing high order ABCs.

Fig. 1

A fictitious domain and the $Q_3^*$-grid with the Cartesian grid in $\Omega _1$ and the radial grid in $\Omega _2$. In this example the boundary layer region contains a single radial layer

In $\Omega _1 \cup \Omega _2$ the equation (1.1) can be reformulated as follows with a proper ABC:

$$\begin{aligned} \Delta u^1 +\omega ^2 u^1= & {} 0 \quad \text {in } \Omega _1,\end{aligned}$$

(1.2a)

$$\begin{aligned} \Delta u^2 +\omega ^2 u^2= & {} 0 \quad \text {in } \Omega _2,\end{aligned}$$

(1.2b)

$$\begin{aligned} u= & {} g \quad \text {on } \Gamma _1, \end{aligned}$$

(1.2c)

$$\begin{aligned} \frac{\partial u^1}{\partial \nu _1} + \frac{\partial u^2}{\partial \nu _2}= & {} 0 \quad \text {on } \Gamma _{12}, \end{aligned}$$

(1.2d)

$$\begin{aligned} \mathcal B (u)= & {} 0 \quad \text {on } \Gamma _2. \end{aligned}$$

(1.2e)

Here,

$$\begin{aligned} \Delta u^1 = u^1_{xx} + u^1_{yy}, \quad \Delta u^2 = u^2_{rr} + \frac{1}{r} u^2_r + \frac{1}{r^2} u^2_{tt}, \end{aligned}$$

the unit outward normal vector $\nu _i$ on $\Gamma _{12}$ is emanating from $\Omega _i$, and (r, t) is the polar coordinate for $\Omega _2$. The interface $\Gamma _{12}$ is a polygon, and it is designed to change according to the mesh refinement in $\Omega _1$. As a mesh becomes finer $\Gamma _{12}$ converges to a circle. Figure 1 represents a simple grid generation of $\Omega _1$ and $\Omega _2$. For $\Omega _1$ the mesh is composed of rectangles (in the interior of $\Omega _1$) and trapezoids (adjacent to $\Gamma _{12}$). The radial mesh for $\Omega _2$ should be constructed subordinately to the mesh in $\Omega _1$. The advantage of considering two separate subdomains is that the inner boundary of a general shape can be treated somehow well with the Cartesian grid and the high order ABC can be more easily applied on a radial grid.

In this paper a new absorbing boundary condition (that is named the discrete radial ABC) is introduced for the Laplace and Helmholtz equations. To derive the discrete ABC we follow the idea of the Bayliss–Gunzburger–Turkel (BGT) [3] absorbing boundary condition. To the author’s knowledge there has not been much attention to the ABCs for frequency domain problems. However, the frequency domain approach on a parallel computing environment can provide very efficient numerical solvers. On the other hand there have been many efforts for construction of the ABCs for the time dependent wave equations. Engquist and Majda [5] made a pioneering work, in which the ABC is obtained by considering waves that enter or leave the domain and annihilating those scattered waves entering the domain from the outside. Bayliss and Turkel [2] constructed a sequence of absorbing boundary conditions for the wave equation, based on annihilation of first several negative radial power terms in the multipole expansion of a solution, and those idea were exploited later to derive the BGT condition with Gunzburger for the static elliptic and wave equations. The high order derivative term of the ABC in [2] can be impractical for implementation, and Hagstrom and Hariharan [7] developed the ABCs that contain only first order derivatives at a cost of auxiliary functions. Huan and Thompson [9] developed these ideas further to obtain the ABCs applicable in the finite element method in a symmetric way. Higdon [8] obtained absorbing boundary conditions by invoking to the finite time difference rather than the differential equation, which improved convergence quality of numerical solutions. Our discrete radial ABC is also obtained by treating the annihilation condition of the BGT condition directly in the radial finite difference equation. For absorbing boundary conditions with elliptic or general shaped obstacles we refer to [1, 13, 14]. For a brief review on the various ABCs we refer to [6] and references therein.

For a numerical method of partial differential equations we consider the hybrid spectral difference method (HSD). The HSD can be understood as the finite difference version of the hybridized Galerkin method. The HSD is simple to implement and it has several advantages over the conventional finite difference methods. The method can be applied to nonuniform grids, retaining the optimal order of convergence, and numerical methods with an arbitrarily high-order convergence can be obtained easily. Problems on a complicated geometry can be treated reasonably well, and the boundary condition can be imposed exactly on the exact boundary. The mass conservation property holds in each cell and flux continuity holds across inter-cell boundaries. Embedded static condensation property considerably reduces global degrees of freedom [10,11,12].

The aim of this paper is to introduce the discrete radial ABC and the hybrid spectral difference method for elliptic equations. The hybrid spectral difference method can manage reasonably well obstacles of a general shape in scattering problems. The fictitious boundary can be taken as a circle, independently of the shape of obstacles, which makes easy the implementation of the discrete radial ABC of a high order.

The paper is organized as follows. In Sect. 2 we review the Bayliss–Gunzburger–Turkel absorbing condition, and the discrete radial ABC is introduced by following the annihilation idea of them. The high order radial derivatives in the BGT condition may not be approximated efficiently in the finite difference setting when the wave number is large. With the discrete radial ABC an exact annihilation is accomplished. In Sect. 3 unique solvability and convergence analysis on an annulus region are presented, and the proofs follow closely the ideas in [3]. In Sect. 4 the HSD on the rectangular grid with the Cartesian coordinate is introduced. The HSD in the polar grid can be derived in a similar manner and we delete details. Section 5 is devoted to numerical experiments for the exterior harmonic and Helmholtz equations. Some comparisons between the BGT condition and discrete radial ABC are made. It is shown that the discrete radial ABC produces quite accurate numerical solutions even for the wave equation of a large wave number. A scattering problem with a scatterer of a general shape is tested, which justify that our new method can be an effective numerical solver for a class of scattering problems.

2 Absorbing Boundary Conditions on the Boundary Layer

In this section we review the Bayliss–Gunzbuger–Turkel (BGT) absorbing boundary condition, and a new absorbing boundary condition (the discrete radial ABC) is proposed. The discrete radial ABC bears the same idea of the BGT condition, and it can be more easily implemented for a high order method. Moreover, convergence looks better than that of the BGT condition in finite difference settings.

2.1 The BGT Absorbing Boundary Condition for the Laplace Equation

For the Laplace equation on an exterior domain, it has the multipole expansion,

$$\begin{aligned} u(r, t) = \sum _{k=1}^\infty \phi _k (t) r^{-k}, \end{aligned}$$

where $\phi _k (t) \in span \{ \cos kt, \ \sin kt \}$. Simple calculation yields that

$$\begin{aligned} \left( r \frac{\partial }{\partial r} + j\right) r^k = (k+j) r^k, \quad -\infty< k < \infty . \end{aligned}$$

Let us define $\mathcal B_m : = \Pi _{j=1}^{m-1} \left( r \frac{\partial }{\partial r} + j \right)$. Then, it is easy to see that

$$\begin{aligned} \mathcal B_m \left( r^k\right) = p_k r^{k}, \quad p_k:= \Pi _{j=1}^{m-1} (k+j), \quad -\infty< k < \infty . \end{aligned}$$

Therefore,

$$\begin{aligned} \mathcal B_m ( u) = \sum _{k=m}^\infty p_{-k} \phi _k (t) r^{-k} \end{aligned}$$

since $p_{-k} =0$ for $1 \le k \le m-1$. The boundary condition on $\Gamma _2$ in (1.2) is imposed as $\mathcal B_m(u)=0$. Hence, we have the error estimate;

$$\begin{aligned} | \mathcal B_m u(r_0, t) | \le O\left( r_0^{-m}\right) \quad \text {on } \Gamma _2, \end{aligned}$$

where $r_0$ is the radius of $\Gamma _2$.

2.2 The BGT Absorbing Boundary Condition for the Helmholtz Eqution

For the Helmholtz equation on an exterior domain the solution has the multipole expansion such that

$$\begin{aligned} u(r,t)= & {} H_0(\omega r) \sum _{k=0}^\infty \frac{\psi _{0,k}(t)}{r^k}+ H_1(\omega r) \sum _{k=0}^\infty \frac{\psi _{1,k}(t)}{r^k} \\\sim & {} \sqrt{\frac{2}{\pi \omega }} e^{i(\omega r -\pi /4)} \sum _{k=0}^\infty \phi _k (t) r^{-k-1/2}. \end{aligned}$$

Here, $H_0$ and $H_1$ are the Hankel functions of the first kind of orders 0 and 1, respectively. The asymptotic expansion is due to [4]. Let us introduce the operator,

$$\begin{aligned} \mathcal B_m u = \Pi _{j=0}^{m-2} \left( r \left( \frac{\partial }{\partial r} - i \omega \right) +j+\frac{1}{2} \right) u. \end{aligned}$$

(2.1)

By the same way as the above, it can be shown that

$$\begin{aligned} \left( r \left( \frac{\partial }{\partial r} - i \omega \right) +j + \frac{1}{2} \right) \left( e^{i \omega r} r^{k-1/2}\right) = (k+j)e^{i \omega r} r^{k-1/2}, \quad -\infty< k < \infty . \end{aligned}$$

Therefore,

$$\begin{aligned} \mathcal B_m \left( e^{i \omega r} r^{k-1/2}\right) = q_k e^{i \omega r} r^{k-1/2}, \quad q_k = \Pi _{j=0}^{m-2} (k+j), \quad -\infty< k < \infty . \end{aligned}$$

Trivially, we have

$$\begin{aligned} \mathcal B_m u \sim \sqrt{\frac{2}{\pi \omega }} e^{i(\omega r -\pi /4)} \sum _{k=m-1}^\infty q_{-k} \phi _k (t) r^{-k-1/2} \end{aligned}$$

since $q_{-k}=0$ for $0 \le k \le m-2$. The error estimate holds;

$$\begin{aligned} | \mathcal B_m u(r_0, t) | \le O\left( r_0^{-m+1/2}\right) \quad \text {on } \Gamma _2. \end{aligned}$$

2.3 The Discrete Radial Absorbing Boundary Condition

We consider a multipole expansion of a solution in the form:

$$\begin{aligned} u(r, t) = g(r) \sum _{k=0}^\infty f_k (t) r^{-\alpha _k}, \quad 0< \alpha _1< \alpha _2< \cdots< \alpha _k < \cdots \end{aligned}$$

where $\Vert g\Vert _\infty < \infty$ and $\Vert f_k \Vert _\infty < \infty$.

Suppose $\{ (\tau _1,t), (\tau _2,t), \ldots , (\tau _{m},t) \} \subset \Omega _2$ are the grid points on the ray with an angle t emanating from the origin with $(\tau _m, t) \in \Gamma _2$. Note that $r_0=\tau _m$ is the radius of the circle $\Gamma _2$. We consider the discrete radial ABC operator as follows:

$$\begin{aligned} \mathcal R_m^h u (r_0, t) = \sum _{j=1}^m c_j u(\tau _j, t) \end{aligned}$$

(2.2)

such that the coefficients, $\{c_j\}_{j=1}^m$ satisfy

$$\begin{aligned}&c_1 g(\tau _1) \tau _1^{-\alpha _1} + c_{2} g(\tau _2) \tau _2^{-\alpha _1} + \cdots + c_m g(\tau _m) \tau _m^{-\alpha _1} = 0 \nonumber \\&c_1 g(\tau _1) \tau _1^{-\alpha _2} + c_{2} g(\tau _2) \tau _2^{-\alpha _2} + \cdots + c_m g(\tau _m) \tau _m^{-\alpha _2} = 0\nonumber \\&\cdots \nonumber \\&c_1 g(\tau _1) \tau _1^{-\alpha _{m-1}} + c_{2} g(\tau _2) \tau _2^{-\alpha _{m-1}} + \cdots + c_m g(\tau _m) \tau _m^{-\alpha _{m-1}} = 0 \nonumber \\&c_1 g(\tau _1) \tau _1^{-\alpha _m} + c_{2} g(\tau _2) \tau _2^{-\alpha _m} + \cdots + c_m g(\tau _m) \tau _m^{-\alpha _m} = g(r_0) r_0^{-\alpha _m}. \end{aligned}$$

(2.3)

Suppose $|r_0 - \tau _1| \ll 1$, then $\mathcal R_m^h u$ satisfy the following estimate:

$$\begin{aligned} \mathcal R_m^h u (r_0, t) = f_{m}( t) g(r_0) r_0^{-\alpha _m} + \sum _{k=m+1}^\infty z_k f_k(t) \tau _1^{-\alpha _k} = O\left( r_0^{-\alpha _m}\right) \end{aligned}$$

with

$$\begin{aligned} z_k = \sum _{j=1}^m c_j g(\tau _j) \left( \frac{\tau _1}{\tau _j}\right) ^{\alpha _k}. \end{aligned}$$

It is worth to note that $|z_k | \le \Vert g \Vert _{\infty } \sum _{j=1}^m |c_j|$ because $|\frac{\tau _1}{\tau _j} | \le 1$. The boundary condition in (1.2) on $\Gamma _2$ will be replaced by $\mathcal R_m^h u=0$.

Table 1 FD approximation of the BGT ABC: $\omega =1$

Table 2 FD approximation of the BGT ABC: $\omega =10$

Table 3 FD approximation of the discrete radial ABC: $\omega =10$

Tables 1, 2, 3 show numerical approximation properties of the BGT and discrete radial ABCs. We consider the radial grid on annulus $1< r < r_0 (=3)$. The finite difference approximation $\mathcal B_m^h u (m=2,3)$ of $\mathcal B_m u$ in (2.1) and the $\mathcal R_m^h u (m=2,3)$ are evaluated with the function values at the Gauss–Legendre points and end points of an interval $[r_0-h, r_0]$;

$$\begin{aligned} \{\tau _1, \tau _2, \ldots , \tau _5\} = \left\{ r_0-h, r_0-h \left( \frac{1}{2} +\frac{\sqrt{3/5}}{2} \right) , r_0-\frac{h}{2}, r_0- h \left( \frac{1}{2}-\frac{\sqrt{3/5}}{2}\right) , r_0 \right\} \end{aligned}$$

with $h=(r_0-1)/N$. For $\mathcal B_m^h$ and $\mathcal R_m^h$ to be good approximations they must satisfy

$$\begin{aligned}&\mathcal B_m^h \left( e^{iwr} r^{-k-1/2}\right) \approx 0, \\&\mathcal R_m^h \left( e^{iwr} r^{-k-1/2}\right) \approx 0 \end{aligned}$$

for $0 \le k \le m-2$. As shown in Tables 1, 2 the finite difference (FD) approximation of the BGT condition induces a lot of error for a high wave number $\omega$ since the FD approximation of high order derivatives in the BGT condition is not accurate enough. For this reason it is recommended in [3] to use the ABC condition

$$\begin{aligned} \mathcal B_2 u = k_1 \frac{\partial u}{\partial r} + \frac{k_2}{\sin t} \frac{\partial }{\partial t} \left( \sin t \frac{\partial u}{\partial t} \right) + k_3 u =0, \end{aligned}$$

where the constants $k_1, k_2, k_3$ depend only on $\omega$ and $r_0$ when u satisfies the Helmholtz equation. It is obtained by substituting $u_{rr}$ in $\mathcal B_2 (u)$ [Eq. (2.1) ] with $u_{rr} = -\frac{1}{r} u_r - \frac{1}{r^2} u_{tt} - \omega ^2 u$.

On the other hand the discrete ABC (2.2) approximate the absorbing boundary condition exactly as shown in Table 3.

Remark 2.1

For the Laplace equation we have $g=1$ and $\alpha _k =k$ in (2.3). Let $\xi _j=\frac{\tau _j}{r_0}$. Then, (2.3) becomes

$$\begin{aligned}&c_1 \xi _1^{-1} + c_2 \xi _2^{-1} + \cdots + c_m \xi _m^{-1} = 0 \nonumber \\&c_1 \xi _1^{-2} + c_2 \xi _2^{-2} + \cdots + c_m \xi _m^{-2} = 0\nonumber \\&\cdots \nonumber \\&c_1 \xi _1^{-m+1} + c_2 \xi _2^{-m+1} + \cdots + c_m \xi _m^{-m+1} = 0 \nonumber \\&c_1 \xi _1^{-m} + c_2 \xi _2^{-m} + \cdots + c_m \xi _m^{-m} = 1. \end{aligned}$$

(2.4)

Let $h=\frac{r_0-\tau _1}{r_0}$. Since the abscissas $\{\xi _j\}_{j=1}^m$ on $[1-h, 1]$ is dependent only on m and h( note that $\{\xi _j\}_{j=1}^{m-1}$ are fixed as the Gauss–Legendre points on the interval $[1-h,1]$) the coefficients $\{c_j\}_{j=1}^m$ are functions of (m, h).

3 Solvability and Convergence Analysis

In this section we provide the unique solvability and convergence analysis for the discrete radial ABC of the exterior Laplace equation on an annulus region. The analysis closely follows those ideas in [3]. It must be possible to extend those analysis to the case of the Helmholtz equation. For simplicity of analysis we consider the fictitious domain as an annulus, $1< r < r_0$.

Theorem 3.1

Suppose $0 < r_0-\tau _1 \ll 1$, where $\{ \tau _j\}_{j=1}^m$ with $\tau _m=r_0$ are abscissas to define the discrete radial ABC. Assume

$$\begin{aligned} \mu _k \equiv \frac{\sum _{j=1}^m c_j \left( \frac{\tau _j}{ \tau _1} \right) ^{-k}}{\sum _{j=1}^m c_j \left( \frac{\tau _j}{r_0} \right) ^{k}} (\tau _1 r_0)^{-k} \ne 1 \end{aligned}$$

for $k \ge m$. Then, the Laplace equation on an annulus $1< r < r_0$ with the Dirichlet data on the inner boundary and the discrete radial ABC on the outer boundary is uniquely solvable. Here the coefficients, $\{ c_j \}_{j=1}^m$ are those in Eq. (2.4).

Proof

The solution of the Laplace equation on the annulus region has the representation in the polar coordinate system as follows:

$$\begin{aligned} u(r,t)=\sum _{k=-\infty }^\infty \phi _k(t) r^k, \end{aligned}$$

where (r, t) is the polar coordinate and $\phi _k(t) = c_k \cos kt +d_k \sin kt$. We will show that the trivial boundary condition induces the trivial solution. On the boundary we have that

$$\begin{aligned} u(1,t)= & {} \sum _{k=1}^{\infty } \phi _{-k} (t) + \sum _{k=0}^\infty \phi _k(t) =0, \quad \text {on } \Gamma _1, \\ \mathcal R^h_m u (r_0,t)= & {} \sum _{k=m}^{\infty } d_{-k} \phi _{-k} (t) r_0^{-k} + \sum _{k=0}^\infty d_k \phi _k(t) r_0^k=0, \quad \text {on } \Gamma _2, \end{aligned}$$

where $d_k = \sum _{j=1}^m c_j (\frac{\tau _j}{r_0} ) ^k$. Solving the above equation, we obtain that

$$\begin{aligned} \phi _0= & {} 0, \ \phi _k=-\phi _{-k}, 1 \le k \le \infty \\ \phi _k= & {} 0, k=1,\ldots , m-1 \\ \phi _k+ & {} \frac{d_{-k}}{d_k} r_0^{-2k} \phi _{-k}=0, m \le k \le \infty . \end{aligned}$$

It is trivial that $\phi _k=0$ for $-m+1 \le k \le m-1$. Let

$$\begin{aligned} \mu _k = \frac{d_{-k}}{d_k} r_0^{-2k} = \frac{\sum _{j=1}^m c_j \left( \frac{\tau _j}{ \tau _1} \right) ^{-k}}{\sum _{j=1}^m c_j \left( \frac{\tau _j}{r_0} \right) ^{k}} (\tau _1 r_0)^{-k}. \end{aligned}$$

Then, we have $\phi _k = \mu _k \phi _{k}$, which implies that $\phi _k=0$ for $m \le k < \infty$ if $\mu _k \ne 1$. It follows immediately that $\phi _{-k}=0$ for $m \le k < \infty$. As a conclusion $\phi _k=0$, $-\infty< k < \infty$. $\square$

Remark 3.2

In the proof of the above theorem we have

$$\begin{aligned} \sum _{j=1}^m c_j \left( \frac{\tau _j}{\tau _1} \right) ^{-k} \rightarrow c_1, \quad \sum _{j=1}^m c_j \left( \frac{\tau _j}{r_0} \right) ^{k} \rightarrow c_m \end{aligned}$$

as $k \rightarrow \infty$. Hence,

$$\begin{aligned} \mu _k \rightarrow 0, \quad k \rightarrow \infty . \end{aligned}$$

Then, there exists $k_0 > 0$ such that $| \mu _k | < 1$ for all $k \ge k_0$. Therefore, the assumption in Theorem 3.1 is reasonable.

Theorem 3.3

Suppose u be the solution of the Laplace equation on an exterior domain $1< r < \infty$ and w be the solution of the Laplace equation on an annulus $1< r < r_0$ with the Dirichlet data $w=u$ on the inner boundary $\Gamma _1$ and the discrete radial ABC on the outer boundary $\Gamma _2$. Under the same assumption as in Theorem 3.1 we have the error estimate

$$\begin{aligned} \left( \int _{\Gamma _2} |u-w|^2 ds \right) ^{1/2}\le & {} C r_0^{-m} \left( \int _{\Gamma _1} |u|^2 ds \right) ^{1/2}. \end{aligned}$$

Proof

The exact solution u and its approximation w by the discrete radial ABC have the multipole expansions,

$$\begin{aligned} u(r,t)=\sum _{k=1}^{\infty } \phi _{-k}(t) r^{-k}, \quad w(r,t)=\sum _{k=-\infty }^\infty \psi _{k}(t) r^k. \end{aligned}$$

Remember that

$$\begin{aligned} \mathcal R_m^h u (r_0,t) = \sum _{k=m}^{\infty } d_{-k} \phi _{-k}(t) r_0^{-k}, \end{aligned}$$

where $d_k=\sum _{j=1}^m c_j (\frac{\tau _j}{r_0} ) ^k$. Define the error,

$$\begin{aligned} e(r,t) = w(r,t)-u(r,t) = \sum _{k=1}^{\infty } \gamma _{-k}(t) r^{-k} + \sum _{k=0}^{\infty } \psi _k(t) r^k \end{aligned}$$

with $\gamma _{-k}=\psi _{-k}-\phi _{-k}$. The boundary conditions, $\mathcal R_m^h w (r_0,t)=0$ and $e(1,t)=0$, yield that

$$\begin{aligned}&\sum _{k=1}^{\infty } \gamma _{-k} (t) + \sum _{k=0}^\infty \psi _k(t) = 0 \quad \text {on } \Gamma _1, \end{aligned}$$

(3.1a)

$$\begin{aligned}&\sum _{k=m}^{\infty } d_{-k} \gamma _{-k} (t) r_0^{-k} + \sum _{k=0}^\infty d_k \psi _k(t) r_0^k = -\sum _{k=m}^{\infty } d_{-k} \phi _{-k}(t) r_0^{-k} \quad \text {on } \Gamma _2. \end{aligned}$$

(3.1b)

From the Eqs. (3.1) and (3.1b) we have

$$\begin{aligned}&\psi _0 =0 , \\&\psi _k=-\gamma _{-k}, \ 1 \le k \le \infty , \\&\psi _{k}=0, \ 0 \le k \le m-1, \\&d_{-k} \gamma _{-k} r_0^{-k} + d_k \psi _k r_0^k = - d_{-k} \phi _{-k} r_0 ^{-k}, \ m \le k < \infty . \end{aligned}$$

The above can be summarized as follows:

$$\begin{aligned} \psi _0=0, \quad \psi _k=\gamma _{-k} =0, \ 1 \le k \le m-1, \quad \psi _k=-\gamma _{-k}, \ m \le k < \infty \end{aligned}$$

and

$$\begin{aligned} \gamma _{-k} \left( d_{-k} r_0^{-k} - d_k r_0^k\right) = -d_{-k} \phi _{-k} r_0^{-k}, \quad m \le k < \infty . \end{aligned}$$

Therefore,

$$\begin{aligned} e(r,t) = \sum _{k=m}^{\infty } \gamma _{-k}(t) r^{-k} - \sum _{k=m}^{\infty } \gamma _{-k}(t) r^k. \end{aligned}$$

Simple calculation yields that

$$\begin{aligned} | d_{-k} | \le C_1 \tau _1^{-k} r_0^k, \quad | d_k | \le C_2, \quad k \ge 0. \end{aligned}$$

Then, we have

$$\begin{aligned} |\gamma _{-k}|= & {} \frac{|d_{-k}|}{ |d_{-k} r_0 ^{-2k} - d_k|} r_0 ^{-2k} |\phi _{-k}|, \quad m \le k < \infty \\\le & {} C (\tau _1 r_0)^{-k} |\phi _{-k}|. \end{aligned}$$

Hence,

$$\begin{aligned} |e(r_0,\cdot )|\le & {} C \left\{ \sum _{k=m}^{\infty } r_0^k (\tau _1 r_0) ^{-k}|\phi _{-k}| + \sum _{k=m}^{\infty } (\tau _1 r_0) ^{-k} r_0 ^{-k} |\phi _{-k}| \right\} . \end{aligned}$$

We arrive at the conclusion that

$$\begin{aligned} \left( \int _{\Gamma _2} |e|^2 ds \right) ^{1/2}\le & {} C r_0^{-m} \left( \int _{\Gamma _1} |u|^2 ds \right) ^{1/2} \end{aligned}$$

if $0 < r_0-\tau _1 \ll 1$ and $r > 1$. $\square$

4 Hybrid Finite Difference Methods

As mentioned in Sect. 1 the domain $\Omega =\Omega _1 \cup \Omega _2$ is a multiply connected domain with the inner boundary $\Gamma _1$, the outer boundary $\Gamma _2$ and the interface $\Gamma _{12}$. To define the hybrid difference method (HDM) we need a quasi-rectangular partition of the subdomain $\Omega _1$. Here, the quasi-rectangle includes a rectangle, a trapezoid (Fig. 3) or a trapezoid-like mesh with one rounded side (Fig. 4). For the subdomain $\Omega _2$ we consider a radial subdivision by polar rectangles. In this section we describe the HDM in the Cartesian coordinate system because the hybrid difference in the polar coordinate can be obtained analogously. The hybrid spectral difference method (HSD) is a high order version of the hybrid difference method.

Let $K_h$ denote the skeleton of a mesh generation $\mathcal {T}_h$ of $\Omega$, and let $\mathcal N(\Omega )$ and $\mathcal N(K_h)$ denote the set of grid points in the closure of a domain and that on its skeleton, respectively. It is worth to note that the mesh is composed mostly of rectangles. However, we need trapezoidal meshes to match the interface $\Gamma _{12}$ and we may need rounded trapezoidal meshes to match $\Gamma _1$ if $\Gamma _1$ is curved.

We call the grid configuration in Fig. 2 as the $Q_2^*$ grid and the grid configuration in Fig. 3 as the $Q_4^*$ grid. The $Q_m^*$ grid denotes the grid configuration obtained from the $Q_m$ grid by deleting four vertices, where the $Q_m$ grid represents the grid on which the binomials of degree up to m ($Q_m$ ) can be uniquely defined. In the HDM the nodes are the Gauss–Legendre points in a cell and its edges.

Fig. 2

The $Q_2^*$ grid: $|R_1|=h_1 \times k_1$, $|R_2|=h_2 \times k_1$, $|R_3|=h_1 \times k_2$

Let us begin with the simplest hybrid difference method (HDM) in the Cartesian coordinate system. The derivation is based on the grid configuration in Fig. 2. The hybrid difference method for the Eq. (1.1) is composed of two kind of finite differences, the cell finite difference and the interface finite difference as follows. The cell finite difference approximates the PDE at the interior cell point so that

$$\begin{aligned} \Delta ^h u (\eta _4) + \omega ^2 u (\eta _4) = \frac{u(\eta _3) -2u(\eta _4) +u(\eta _5)}{(h_1/2)^2} + \frac{u(\eta _8) -2 u(\eta _4) +u(\eta _1)}{(k_1/2)^2} + \omega ^2 u (\eta _4) = 0 \end{aligned}$$

(4.1)

on the cell $R_1$, and the interface finite difference approximates the flux continuity at the intercell point so that

$$\begin{aligned}{}[[ \partial _\nu ^h u ]]_{\eta } = \left\{ \begin{array}{l} \frac{ 3 u(\eta _5) - 4 u(\eta _4) + u(\eta _3)}{h_1} + \frac{ 3 u(\eta _5) - 4 u(\eta _6) + u(\eta _7)}{h_2} =0, \quad \eta =\eta _5\\ \frac{ 3 u(\eta _8) - 4 u(\eta _4) + u(\eta _1)}{k_1} + \frac{ 3 u(\eta _8) - 4 u(\eta _{11}) + u(p_{13})}{k_2}= 0, \quad \eta =\eta _8 \end{array} \right. . \end{aligned}$$

(4.2)

Here, $\partial _\nu ^h u = \nabla ^h u \cdot \nu$, and $\nu$ is the outward unit normal vector from each cell. The cell finite difference (4.1) can be solved for $u(\eta _4)$ in terms of the cell boundary values,

Fig. 3

A $Q_4^*$-rectangular and trapezoidal grids: The four vertices $\{ \eta _{jk}: i,j=0, 4\}$ are not used in computation. The interior grids are the Gauss–Legendre points of a rectangle

Fig. 4

The $Q_3^*$ grid generation around the obstacle with a curved boundary; the dotted is the line of integration

$\{ u(\eta _1), u(\eta _3), u(\eta _5), u(\eta _8)\}$ for each cell. Then, the interface difference (4.2) yields the global stiffness system with unknowns $\{ u (\eta ): \eta \in \mathcal N (K_h) \}$. Therefore, the static condensation property is naturally embedded in the HDM.

To derive a higher order method we consider a more complicated cell configuration as in Fig. 3. Then, the cell finite difference solves the cell problem:

$$\begin{aligned} \Delta ^h u_h (\eta ) + \omega ^2 u_h (\eta ) = 0, \quad \eta \in \mathcal N(\Omega ) {\setminus } \mathcal N(K_h), \end{aligned}$$

(4.3)

and the interface finite difference solves the interface condition

$$\begin{aligned}{}[[ \partial _\nu ^h u_h]]_\eta = 0, \quad \eta \in \mathcal N(K_h){\setminus } \Gamma . \end{aligned}$$

(4.4)

For a detailed derivation of the high order finite difference formulas for $\Delta ^h$ and $\partial _\nu ^h$ we refer to [11, 12]. Let us define the Gaussian quadratures on a reference cell R (with $|R|=h\times k$) and its boundary $\partial R$ on the $Q_m^*$ grid as follows:

$$\begin{aligned} (f,g)_{R,h}&= \frac{ h k}{4} \sum _{i=1}^{m-1} \sum _{j=1}^{m-1} \sigma _i \sigma _j f(\eta _{ij}) g(\eta _{ij}), \\ \langle f,g\rangle _{\partial R,h}&= \frac{k}{2} \sum _{j=1}^{m-1} \sigma _j \left( f(\eta _{0j}) g(\eta _{0j}) + f(\eta _{mj}) g(\eta _{mj})\right) \\&\quad + \frac{h}{2} \sum _{j=1}^{m-1} \sigma _j \left( f(\eta _{j0}) g(\eta _{j0}) + f(\eta _{jm}) g(\eta _{jmj})\right) . \end{aligned}$$

Here, $\{\sigma _j\}_{j=1}^{m-1}$ is the Gaussian weights on the reference interval $[-1, 1]$. There exists a natural composite quadrature defined on the whole domain $\Omega$ as follows.

$$\begin{aligned} (f,g)_h = \sum _{R \in \mathcal {T}_h} (f,g)_{R,h}. \end{aligned}$$

Then, the Eqs. (4.3) and (4.4) can be unified in a variational form:

$$\begin{aligned} - (\Delta ^h u_h + \omega ^2 u_h, v)_{h} + \sum _{R \in \mathcal {T}_h} \langle \partial _\nu ^h u_h, v\rangle _{\partial R, h} = 0, \quad v \in C_0(\Omega ). \end{aligned}$$

(4.5)

Some numerical analysis of (4.5) can be found in [11], where analysis is performed for the Poisson equation. The hybrid difference method is understood as the finite difference version of the hybridized finite element method. The main advantage of the HDM is that the finite differences are of one dimensional nature (it is not related to two or three dimensional polynomial interpolation). Therefore, we can handle the boundary data exactly even on a domain with a curved boundary by extending the line of derivative evaluation up to the given curved boundary and taking the intersection as a nodal point (see Fig. 4). Secondly, the method possesses the embedded static condensation property, which considerably reduces global degrees of freedom in the global stiffness system.

Table 4 Reduction in degrees of freedom by static condensation

Remark 4.1

The subdomain $\Omega _2$ can contain one or two layers of polar (quasi) rectangles. To combine a low order HDM and a high order ABC we need two layers, and just one layer is enough for combination of the $Q_m^*$ grid HDM and the $\mathcal R_n^h$- ABC if $n \le m+1$.

Remark 4.2

Suppose a domain is the unit square with a $N\times N$-rectangular partition. Table 4 highlights reduction in degrees of freedom by the static condensation. The reduction rate is computed asymptotically under the assumption that N is a big number.

5 Numerical Experiments

In this section we provide numerical experiments on three regions:

• An annulus with $1< r < \frac{3}{2}$,

• A Chinese coin (see Fig. 1) bounded by $\Gamma _1 = \{ \max \{|x|,|y|\}=1 \}$ and $\Gamma _2 = \{ |r|=3\}$,

• The domain “D” bounded by $\Gamma _1 = \{ x=-1, \ |y| = 1, \ x^2 + y^2 = 1 \}$ and $\Gamma _2 = \{ |r|=3\}$.

Fig. 5

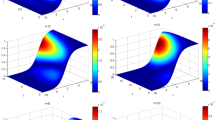
Comparison of convergence properties of the discrete radial ABC (left) and BGT ABC (right): the Laplace equation on the $Q_2^*\hbox { grid}$ (above) and $Q_4^*\hbox { grid}$ (below) (Example 1)

Here, $\mathcal R_m^h u =0$ and $\mathcal B_m^h u=0$ are called the m-th order ABC. The first observation was comparison of condition numbers for the discrete and BGT ABCs. Both methods yield similar condition numbers and we omit details.

Example 1

We consider the Laplace equation with the exact solution:

$$\begin{aligned} u(x,y) = \frac{1}{2} \left( \log |\left( x-\frac{1}{2}\right) ^2 + y^2| - \log |x^2 + y^2 | \right) \end{aligned}$$

on the annulus. The convergence properties are compared for $\mathcal R_{m}^h(u)=0$ and $\mathcal B_m^h(u)=0$ with $m=2 \sim 4$ on the radial $Q_2^*$ and $Q_4^*$ grids.

Example 2

We consider the Helmholtz equation with the exact solution:

$$\begin{aligned} u(r,t)) = H_1 (\omega r) \cos (t) \end{aligned}$$

on the annulus. Here, $H_1$ is the Hankel function of the first kind with order one. Only the results for the discrete radial ABC ($\mathcal R_m^h(u)=0$) are presented. This example is to illuminate the sensitivity of the discrete radial ABC depending on change of the wave number $\omega$.

Fig. 6

Convergence history by varying $\omega$ for the Helmholtz equation: the discrete radial ABC on the $Q_2^*$ grid (Example 2)

Fig. 7

Convergence history by varying $\omega$ for the Helmholtz equation: the discrete radial ABC on the $Q_4^*$ grid (Example 2)

Fig. 8

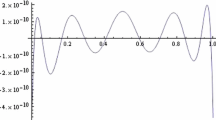
Convergence plot of the real part of the scattered wave with the incident angle, $\alpha =0$. The meshes correspond to the 16, 32, 64 and 128 subdivision of the exterior boundary $\Gamma _2$, respectively (Example 3)

Example 3

The scattering problem with the sound soft boundary condition is solved on the Chinese coin domain. Here, the grids are give as in Fig. 1. The incident wave $u_{in} = e^{-i \omega (x \cos \alpha +y \sin \alpha )}$ with the incident angle $\alpha = 0$ and $\omega =5$ is tested, and the scattered wave is plotted by increasing the degrees of freedom. The 4th order discrete radial ABC (${\mathcal {R}}_4^{h}u =0$) on the $Q_4^*$ grid is used for numerical computation.

Example 4

The scatterer of the shape “D” is tested with the incident wave $u_{in} = e^{-i \omega (x \cos \alpha +y \sin \alpha )}$ and the incident angles $\alpha = 0, \frac{\pi }{4}, \frac{\pi }{2}, \pi$. The same computational parameters are chosen as in Example 3.

Fig. 9

The real part of the scattered waves with the various incident angles, $\alpha =0, \frac{\pi }{4}, \frac{\pi }{2}, \pi$. The mesh corresponds to the 128 subdivision of the exterior boundary $\Gamma _2$ (Example  4)

As shown in Fig. 5 the discrete radial and BGT ABCs perform evenly well for the Laplace equation. The higher order ABC shows better convergence than the lower order ABC. As the mesh becomes finer the error seems to be dominated by the truncation error in the absorbing boundary condition. For the Helmholtz equation numerical examples only with the discrete radial ABC are presented. We observe that the BGT absorbing boundary condition produces spurious numerical solutions because of the poor finite difference approximation property as mentioned in Sect. 2, and we omit it here. As shown in Figs. 6 and 7 the discrete radial ABC performs quite robust even for a larger wave number (in view of the level of discretization). Here, the computation is performed on a $N \times 2N$ mesh by doubling N up to $N=64$ for the radial $Q_2^*$ grid and up to $N=32$ for the radial $Q_4^*$ grid. When the wave number is small the higher order ABC performs clearly better than the lower order ABC. However, convergence property becomes similar regardless of orders of the discrete radial ABC when the wave number increases. Even the 2nd order method $\mathcal R_2^h u=0$ performs the best for the cases, $\omega =50, \ 100$. Nonetheless, the high order hybrid difference combined with the high order discrete radial ABC (for example, the $Q_4^*$ grid method and $\mathcal R_4^h=0$) produces more reliable solutions for a wide range of wave numbers. From those observation the scattering problems in Examples 3 and 4 are solved by using the ABC, $\mathcal R_4^h (u)=0$ on the $Q_4^*$ grid. Figure 8 clearly shows how the scattered wave converges as the degrees of freedom (dof) increase. Figure 9 represents the real part of the scattered wave with various incident angles, and this example shows that our method can manage a complicated geometry-problem quite well. The numerical results accord well with those existing numerical results.