Abstract
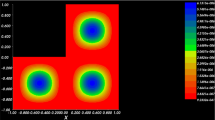
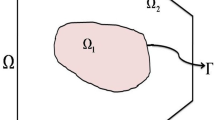
This paper studies a residual-based a posteriori error estimates for linear parabolic interface problems in a bounded convex polygonal domain in \(\mathbb {R}^2\). We use the standard linear finite element spaces in space which are allowed to change in time and the two-step backward differentiation formula (BDF-2) approximation at equidistant time step is used for the time discretizations. The essential ingredients in the error analysis are the continuous piecewise quadratic space–time BDF-2 reconstruction and Scott–Zhang interpolation estimates. Optimal order in time and an almost optimal order in space error estimates are derived in the \(L^{\infty }(L^{2})\)-norm using only energy method. The interfaces are assumed to be of arbitrary shape but are smooth for our purpose. Numerical experiments are performed to validate the asymptotic behaviour of the derived error estimators.


Similar content being viewed by others
References
Adams, R.A., Fournier, J.J.F.: Sobolev Spaces vol. 140 of Pure and Applied Mathematics, 2nd edn. Elsevier, Amsterdam (2003)
Akrivis, G., Chatzipantelidis, P.: A posteriori error estimates for the two-step backward differentiation formula method for parabolic equations. SIAM J. Numer. Anal. 48, 109–132 (2010)
Akrivis, G., Makridakis, C., Nochetto, R.H.: A posteriori error estimates for the Crank–Nicolson method for parabolic equations. Math. Comput. 75, 511–531 (2006)
Bänsch, E., Karakatsani, F., Makridakis, C.: A posteriori error control for fully discrete Crank–Nicolson schemes. SIAM J. Numer. Anal. 50, 2845–2872 (2012)
Becker, J.: A second order backward difference method with variable steps for a parabolic problem. BIT 38, 644–662 (1998)
Bernardi, C., Verfürth, R.: Adaptive finite element methods for elliptic equations with non-smooth coefficients. Numer. Math. 85, 579–608 (2000)
Berrone, S.: Robust a posteriori error estimates for finite element discretizations of the heat equation with discontinuous coefficients. M2AN Math. Model. Numer. Anal. 40, 991–1021 (2006)
Bramble, J.H., Pasciak, J.E., Sammon, P.H., Thomée, V.: Incomplete iterations in multistep backward difference methods for parabolic problems with smooth and nonsmooth data. Math. Comput. 52, 339–367 (1989)
Brenner, S.C., Scott, L.R.: The Mathematical Theory of Finite Element Methods, vol. 15 of Texts in Applied Mathematics, 3rd edn. Springer, New York (2008)
Cai, Z., Ye, X., Zhang, S.: Discontinuous Galerkin finite element methods for interface problems: a priori and a posteriori error estimations. SIAM J. Numer. Anal. 49, 1761–1787 (2011)
Cai, Z., Zhang, S.: Recovery-based error estimator for interface problems: conforming linear elements. SIAM J. Numer. Anal. 47, 2132–2156 (2009)
Chen, Z., Zou, J.: Finite element methods and their convergence for elliptic and parabolic interface problems. Numer. Math. 79, 175–202 (1998)
Ladyženskaja, O.A., Solonnikov, V.A., Ural\(^{\prime }\)ceva, N.N.: Linear and Quasilinear Equations of Parabolic Type. Translated from the Russian by S. Smith. Translations of Mathematical Monographs, vol. 23. American Mathematical Society (1968)
Lakkis, O., Makridakis, C.: Elliptic reconstruction and a posteriori error estimates for fully discrete linear parabolic problems. Math. Comput. 75, 1627–1658 (2006)
Le Roux, M.-N.: Semidiscretization in time for parabolic problems. Math. Comput. 33, 919–931 (1979)
Lumer, G., Weis, L.: Evolution Equations and Their Applications in Physical and Life sciences, vol. 215 of Lecture Notes in Pure and Applied Mathematics. Marcel Dekker, Inc., New York (2001)
Luskin, M., Rannacher, R.: On the smoothing property of the Crank–Nicolson scheme. Appl. Anal. 14, 117–135 (1983)
Makridakis, C., Nochetto, R.H.: Elliptic reconstruction and a posteriori error estimates for parabolic problems. SIAM J. Numer. Anal. 41, 1585–1594 (2003)
McLean, W., Thomée, V.: Numerical solution of an evolution equation with a positive-type memory term. J. Aust. Math. Soc. Ser. B 35, 23–70 (1993)
Reusken, A., Nguyen, T.H.: Nitsche’s method for a transport problem in two-phase incompressible flows. J. Fourier Anal. Appl. 15, 663–683 (2009)
Scott, L.R., Zhang, S.: Finite element interpolation of nonsmooth functions satisfying boundary conditions. Math. Comput. 54, 483–493 (1990)
Sen Gupta, J.: A Posteriori Error Analysis of Finite Elemet Method For Parabolic InterfaceProblems. PhD Thesis, Indian Institute of Technology, Guwahati, India (2015)
Thomée, V.: Galerkin Finite Element Methods for Parabolic Problems, vol. 25 of Springer Series in Computational Mathematics, 2nd edn. Springer, Berlin (2006)
Tu, C., Peskin, C.S.: Stability and instability in the computation of flows with moving immersed boundaries: a comparison of three methods. SIAM J. Sci. Stat. Comput. 13, 1361–1376 (1992)
Verfürth, R.: A posteriori error estimates for finite element discretizations of the heat equation. Calcolo 40, 195–212 (2003)
Acknowledgments
The authors wish to thank both the referees for their valuable comments and suggestions which improve the presentation of the manuscript.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Sen Gupta, J., Sinha, R.K., Reddy, G.M.M. et al. A Posteriori Error Analysis of Two-Step Backward Differentiation Formula Finite Element Approximation for Parabolic Interface Problems. J Sci Comput 69, 406–429 (2016). https://doi.org/10.1007/s10915-016-0203-z
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10915-016-0203-z