Skip to main content
SpringerLink
Log in

Flux Splitting for Stiff Equations: A Notion on Stability

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

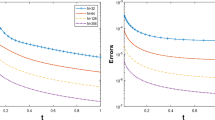
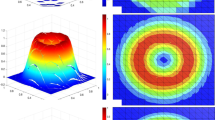
For low Mach number flows, there is a strong recent interest in the development and analysis of IMEX (implicit/explicit) schemes, which rely on a splitting of the convective flux into stiff and nonstiff parts. A key ingredient of the analysis is the so-called Asymptotic Preserving property, which guarantees uniform consistency and stability as the Mach number goes to zero. While many authors have focused on asymptotic consistency, we study asymptotic stability in this paper: does an IMEX scheme allow for a CFL number which is independent of the Mach number? We derive a stability criterion for a general linear hyperbolic system. In the decisive eigenvalue analysis, the advective term, the upwind diffusion and a quadratic term stemming from the truncation in time all interact in a subtle way. As an application, we show that a new class of splittings based on characteristic decomposition, for which the commutator vanishes, avoids the deterioration of the time step which has sometimes been observed in the literature.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

References

  1. Arun, K., Noelle, S.: An asymptotic preserving scheme for low Froude number shallow flows. IGPM Preprint 352 (2012)

  2. Ascher, U., Ruuth, S., Spiteri, R.: Implicit-explicit Runge–Kutta methods for time-dependent partial differential equations. Appl. Numer. Math. 25, 151–167 (1997)

    Article  MATH  MathSciNet  Google Scholar 

  3. Boscarino, S.: Error analysis of IMEX Runge–Kutta methods derived from differential-algebraic systems. SIAM J. Numer. Anal. 45, 1600–1621 (2007)

    Article  MATH  MathSciNet  Google Scholar 

  4. Choi, Y.H., Merkle, C.: The application of preconditioning in viscous flows. J. Comput. Phys. 105(2), 207–223 (1993)

    Article  MATH  MathSciNet  Google Scholar 

  5. Chorin, A.: The numerical solution of the Navier–Stokes equations for an incompressible fluid. Bull. Am. Math. Soc. 73, 928–931 (1967)

    Article  MATH  MathSciNet  Google Scholar 

  6. Colella, P., Pao, K.: A projection method for low speed flows. J. Comput. Phys. 149(2), 245–269 (1999)

    Article  MATH  MathSciNet  Google Scholar 

  7. Cordier, F., Degond, P., Kumbaro, A.: An asymptotic-preserving all-speed scheme for the Euler and Navier–Stokes equations. J. Comput. Phys. 231, 5685–5704 (2012)

    Article  MATH  MathSciNet  Google Scholar 

  8. Courant, R., Friedrichs, K., Lewy, H.: Über die partiellen Differenzengleichungen der mathematischen Physik. Mathematische Annalen 100(1), 32–74 (1928)

    Article  MATH  MathSciNet  Google Scholar 

  9. Crouzeix, M.: Une méthode multipas implicite–explicite pour l’approximation des équations d’évolution paraboliques. Numerische Mathematik 35(3), 257–276 (1980)

    Article  MATH  MathSciNet  Google Scholar 

  10. Degond, P., Lozinski, A., Narski, J., Negulescu, C.: An asymptotic-preserving method for highly anisotropic elliptic equations based on a micro-macro decomposition. J. Comput. Phys. 231, 2724–2740 (2012)

    Article  MATH  MathSciNet  Google Scholar 

  11. Degond, P., Tang, M.: All speed scheme for the low Mach number limit of the isentropic Euler equation. Commun. Comput. Phys. 10, 1–31 (2011)

    MathSciNet  Google Scholar 

  12. Dellacherie, S.: Analysis of Godunov type schemes applied to the compressible Euler system at low Mach number. J. Comput. Phys. 229(4), 978–1016 (2010)

    Article  MATH  MathSciNet  Google Scholar 

  13. Godlewski, E., Raviart, P.A.: Hyperbolic Systems of Conservation Laws. Ellipses, Paris (1991)

    MATH  Google Scholar 

  14. Guillard, H., Murrone, A.: On the behavior of upwind schemes in the low Mach number limit: II. Godunov type schemes. Comput. Fluids 33(4), 655–675 (2004)

    Article  MATH  Google Scholar 

  15. Guillard, H., Viozat, C.: On the behaviour of upwind schemes in the low Mach number limit. Comput. Fluids 28(1), 63–86 (1999)

    Article  MATH  MathSciNet  Google Scholar 

  16. Haack, J., Jin, S., Liu, J.G.: An all-speed asymptotic-preserving method for the isentropic Euler and Navier–Stokes equations. Commun. Comput. Phys. 12, 955–980 (2012)

    MathSciNet  Google Scholar 

  17. Hairer, E., Wanner, G.: Solving Ordinary Differential Equations II. Springer Series in Computational Mathematics (1991)

  18. Jin, S.: Efficient asymptotic-preserving (AP) schemes for some multiscale kinetic equations. SIAM J. Sci. Comput. 21, 441–454 (1999)

    Article  MATH  MathSciNet  Google Scholar 

  19. Jin, S.: Asymptotic preserving (AP) schemes for multiscale kinetic and hyperbolic equations: a review. Rivista di Matematica della Universit di Parma 3, 177–216 (2012)

    MATH  Google Scholar 

  20. Jin, S., Pareschi, L., Toscani, G.: Diffusive relaxation schemes for multiscale discrete-velocity kinetic equations. SIAM J. Numer. Anal. 35, 2405–2439 (1998)

    Article  MATH  MathSciNet  Google Scholar 

  21. Klainerman, S., Majda, A.: Singular limits of quasilinear hyperbolic systems with large parameters and the incompressible limit of compressible fluids. Commun. Pure Appl. Math. 34, 481–524 (1981)

    Article  MATH  MathSciNet  Google Scholar 

  22. Klein, R.: Semi-implicit extension of a Godunov-type scheme based on low mach number asymptotics I: one-dimensional flow. J. Comput. Phys. 121, 213–237 (1995)

    Article  MATH  MathSciNet  Google Scholar 

  23. Klein, R., Botta, N., Schneider, T., Munz, C., Roller, S., Meister, A., Hoffmann, L., Sonar, T.: Asymptotic adaptive methods for multi-scale problems in fluid mechanics. J. Eng. Math. 39(1), 261–343 (2001)

    Article  MATH  MathSciNet  Google Scholar 

  24. Kröner, D.: Numerical Schemes for Conservation Laws. Wiley Teubner, New York (1997)

    MATH  Google Scholar 

  25. Lax, P.: On the stability of difference approximations to solutions of hyperbolic equations with variable coefficients. Commun. Pure Appl. Math. 14, 497–520 (1961)

    Article  MATH  MathSciNet  Google Scholar 

  26. Murrone, A., Guillard, H.: Behavior of upwind scheme in the low Mach number limit: III. Preconditioned dissipation for a five equation two phase model. Comput. Fluids 37(10), 1209–1224 (2008)

    Article  MATH  MathSciNet  Google Scholar 

  27. Noelle, S., Bispen, G., Arun, K., Lukacova-Medvidova, M., Munz, C.D.: An asymptotic preserving all Mach number scheme for the Euler equations of gas dynamics. SIAM J. Sci. Comput. (2014). doi:10.1137/120895627

  28. Richtmyer, R., Morton, K.: Difference Methods for Initial-Value Problems. Krieger Publishing Company, Malabar (1994)

    MATH  Google Scholar 

  29. Russo, G., Boscarino, S.: IMEX Runge-Kutta schemes for hyperbolic systems with diffusive relaxation. In: European Congress on Computational Methods in Applied Sciences and Engineering (ECCOMAS 2012) (2012)

  30. Schütz, J.: An asymptotic preserving method for linear systems of balance laws based on Galerkin’s method. J. Sci. Comput. 60, 438–456 (2014). doi:10.1007/s10915-013-9801-1

    Article  MATH  MathSciNet  Google Scholar 

  31. Strang, G.: Accurate partial difference methods. Numerische Mathematik 6, 37–46 (1964)

    Article  MATH  MathSciNet  Google Scholar 

  32. Turkel, E.: Preconditioned methods for solving the incompressible and low speed compressible equations. J. Comput. Phys. 72(2), 277–298 (1987)

    Article  MATH  Google Scholar 

  33. Warming, R., Hyett, B.J.: The modified equation approach to the stability and accuracy of finite-difference methods. J. Comput. Phys. 14, 159–179 (1974)

    Article  MATH  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Institut für Geometrie und Praktische Mathematik, RWTH Aachen University, Templergraben 55, 52062 , Aachen, Germany

    Jochen Schütz & Sebastian Noelle

Authors
  1. Jochen Schütz
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Sebastian Noelle
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jochen Schütz.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Schütz, J., Noelle, S. Flux Splitting for Stiff Equations: A Notion on Stability. J Sci Comput 64, 522–540 (2015). https://doi.org/10.1007/s10915-014-9942-x

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10915-014-9942-x

Keywords

Mathematics Subject Classification

Search

Navigation