Skip to main content
SpringerLink
Log in

Domain Decomposition Method and High-Order Absorbing Boundary Conditions for the Numerical Simulation of the Time Dependent Schrödinger Equation with Ionization and Recombination by Intense Electric Field

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

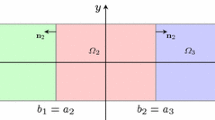
This paper is devoted to the efficient computation of the time dependent Schrödinger equation for quantum particles subject to intense electromagnetic fields including ionization and recombination of electrons with their parent ion. The proposed approach is based on a domain decomposition technique, allowing a fine computation of the wavefunction in the vicinity of the nuclei located in a domain \(\Omega _1\) and a fast computation in a roughly meshed domain \(\Omega _2\) far from the nuclei where the electrons are assumed free. The key ingredients in the method are (i) well designed transmission boundary conditions on \(\partial \Omega _1\) (resp. \(\partial \Omega _2\)) in order to estimate the part of the wavefunction “leaving” Domain \(\Omega _1\) (resp. \(\Omega _2\)), (ii) a Schwarz waveform relaxation algorithm to accurately reconstruct the solution. The developed method makes it possible for electrons to travel from one domain to another without loosing accuracy, when the frontier or the overlapping region between two domains is crossed by the wavefunction.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19

Similar content being viewed by others

References

  1. Alinhac, S., Gérard, P.: Pseudo-Differential Operators and the Nash–Moser Theorem, volume 82 of Graduate Studies in Mathematics. American Mathematical Society, Providence, RI (2007). Translated from the 1991 French original by Stephen S. Wilson

  2. Antoine, X., Arnold, A., Besse, C., Ehrhardt, M., Schädle, A.: A review of transparent and artificial boundary conditions techniques for linear and nonlinear Schrödinger equations. Commun. Comput. Phys. 4(4), 729–796 (2008)

    MathSciNet  Google Scholar 

  3. Antoine, X., Bao, W., Besse, C.: Computational methods for the dynamics of the nonlinear Schrödinger/Gross–Pitaevskii equations. Comput. Phys. Comm. 184(12), 2621–2633 (2013)

    Article  MathSciNet  Google Scholar 

  4. Antoine, X., Barucq, H., Bendali, A.: Bayliss–Turkel-like radiation conditions on surfaces of arbitrary shape. J. Math. Anal. Appl. 229(1), 184–211 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  5. Antoine, X., Besse C.: Construction, structure and asymptotic approximations of a microdifferential transparent boundary condition for the linear Schrödinger equation. J. Math. Pures Appl. (9), 80(7), 701–738 (2001)

  6. Antoine, X., Besse, C.: Unconditionally stable discretization schemes of non-reflecting boundary conditions for the one-dimensional Schrödinger equation. J. Comput. Phys. 188(1), 157–175 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  7. Antoine, X., Besse, C., Klein, P.: Absorbing boundary conditions for the one-dimensional Schrödinger equation with an exterior repulsive potential. J. Comput. Phys. 228(2), 312–335 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  8. Antoine, X., Besse, C., Klein, P.: Absorbing boundary conditions for the two-dimensional Schrödinger equation with an exterior potential. Part I: construction and a priori estimates. Math. Models Methods Appl. Sci. 22(10), 1250026, 38 (2012)

  9. Antoine, X., Besse, C., Klein, P.: Absorbing boundary conditions for the two-dimensional Schrodinger equation with an exterior potential. Part II: discretization and numerical results. Numerische Mathematik 125(2), 191–223 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  10. Antoine, X., Besse, C., Szeftel, J.: Towards accurate artificial boundary conditions for nonlinear PDEs through examples. Cubo 11(4), 29–48 (2009)

    MathSciNet  MATH  Google Scholar 

  11. Bandrauk, A.: Molecules in Laser Fields, Chap. 1. M. Dekker, NY (1994)

  12. Bandrauk, A., Chelkowski, S., Yu, H., Constant, E.: Enhanced harmonic generation in extended molecular systems by two-color excitation. Phys. Rev. A 56, 2537–2540 (1997)

    Article  Google Scholar 

  13. Bandrauk, A.D., Fillion-Gourdeau, F., Lorin, E.: Atoms and molecules in intense laser fields: gauge invariance of theory and models. J. Phys. B-Atom. Mol. Opt. Phys. 46(15), 153001 (2013)

  14. Baskakov, V.A., Popov, A.V.: Implementation of transparent boundaries for numerical solution of the Schrödinger equation. Wave Mot. 14(2), 123–128 (1991)

    Article  MathSciNet  Google Scholar 

  15. Bérenger, J.-P.: A perfectly matched layer for the absorption of electromagnetic waves. J. Comput. Phys. 114(2), 185–200 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  16. Cohen-Tannoudji, C., Dupont-Roc, J., Grynberg, G.: Atom–Photon Interactions. Wiley, NY (1992)

    Google Scholar 

  17. Corkum, P.-B.: Plasma perspective on strong-field multiphoton ionization. Phys. Rev. Lett. 71, 1994–1997 (1993)

  18. Engquist, B., Majda, A.: Absorbing boundary conditions for the numerical simulation of waves. Math. Comp. 31(139), 629–651 (1977)

    Article  MathSciNet  MATH  Google Scholar 

  19. Gander, M., Halpern, L.: Optimized schwarz waveform relaxation methods for advection reaction diffusion problems. SIAM J. Num. Anal. 45(2), 666–697 (2007)

  20. Gander, M.J.: Optimized Schwarz methods. SIAM J. Numer. Anal. 44(2), 699–731 (2006); (electronic)

  21. Gander, M.J., Halpern, L., Nataf, F.: Optimal Schwarz waveform relaxation for the one dimensional wave equation. SIAM J. Numer. Anal. 41(5), 1643–1681 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  22. Hagstrom, T., Tewarson, R.P., Jazcilevich, A.: Numerical experiments on a domain decomposition algorithm for nonlinear elliptic boundary value problems. Appl. Math. Lett. 1(3), 299–302 (1988)

    Article  MathSciNet  MATH  Google Scholar 

  23. Halpern, L., Rauch, J.: Error analysis for absorbing boundary conditions. Numer. Math. 51(4), 459–467 (1987)

    Article  MathSciNet  MATH  Google Scholar 

  24. Halpern, L., Szeftel, J.: Optimized and quasi-optimal Schwarz waveform relaxation for the one-dimensional Schrödinger equation. Math. Models Methods Appl. Sci. 20(12), 2167–2199 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  25. Hörmander, L.: The Analysis of Linear Partial Differential Operators. III. Classics in Mathematics. Springer, Berlin (2007); Pseudo-Differential Operators

  26. Jiang, S., Greengard, L.: Fast evaluation of nonreflecting boundary conditions for the Schrödinger equation in one dimension. Comput. Math. Appl. 47(6–7), 955–966 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  27. Kamta, G.L., Bandrauk, A.D.: High-order harmonic generation from two-center molecules: time-profile analysis of nuclear contributions. Phys. Rev. A 70(1), 011404-1–011404-4 (2004)

  28. Lewenstein, M., Balcou, Ph, Ivanov, MYu., L’Huillier, A., Corkum, P.B.: Theory of high-harmonic generation by low-frequency laser fields. Phys. Rev. A 49(3), 2117–2132 (1994)

    Article  Google Scholar 

  29. Lorin, E., Chelkowski, S., Bandrauk, A.: A numerical Maxwell–Schrödinger model for laser-matter interaction and propagation. Comput. Phys. Comm. 177(12), 908–932 (2007)

    Article  MATH  Google Scholar 

  30. Lorin, E., Chelkowski, S., Bandrauk, A.: Attosecond pulse generation from aligned molecules—dynamics and propagation in H\(_2^+\). New J. Phys. 10, 025033 (2008)

  31. Lorin, E., Chelkowski, S., Bandrauk, A.D.: Mathematical modeling of boundary conditions for laser-molecule time-dependent Schrödinger equations and some aspects of their numerical computation—one-dimensional case. Numer. Methods Partial Differ. Equ. 25(1), 110–136 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  32. Milosevic, D.B., Paulus, G.G., Bauer, D., Becker, W.: Above-threshold ionization by few-cycle pulses. J. Phys. B: Atom. Mol. Opt. Phys. 39(14), R203–R262 (2006)

    Article  Google Scholar 

  33. Strikwerda, J.C.: Finite Difference Schemes and Partial Differential Equations, 2nd ed. Society for Industrial and Applied Mathematics (SIAM), Philadelphia, PA (2004)

  34. Szeftel, J.: Absorbing boundary conditions for one-dimensional nonlinear Schrödinger equations. Numer. Math. 104(1), 103–127 (2006)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgments

The first author thanks the support of the french ANR grants “Bond” (ANR-13-BS01-0009-01) and “BECASIM” (ANR-12-MONU-0007-02). The second and third authors would like to thank NSERC for the financial support.

Author information

Authors and Affiliations

  1. Institut Elie Cartan de Lorraine, Université de Lorraine, 54506 , Vandoeuvre-lès-Nancy Cedex, France

    X. Antoine

  2. Inria Nancy Grand-Est/IECL - ALICE, Vandoeuvre-lès-Nancy Cedex, France

    X. Antoine

  3. Centre de Recherches Mathématiques, Université de Montréal, Montreal, H3T 1J4, Canada

    E. Lorin & A. D. Bandrauk

  4. School of Mathematics and Statistics, Carleton University, Ottawa, K1S 5B6, Canada

    E. Lorin

  5. Laboratoire de Chimie Théorique, Université de Sherbrooke, Sherbrooke, J1K 2R1, Canada

    A. D. Bandrauk

Authors
  1. X. Antoine
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. E. Lorin
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. A. D. Bandrauk
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to E. Lorin.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Antoine, X., Lorin, E. & Bandrauk, A.D. Domain Decomposition Method and High-Order Absorbing Boundary Conditions for the Numerical Simulation of the Time Dependent Schrödinger Equation with Ionization and Recombination by Intense Electric Field. J Sci Comput 64, 620–646 (2015). https://doi.org/10.1007/s10915-014-9902-5

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10915-014-9902-5

Keywords

Search

Navigation