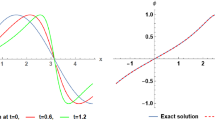
In this paper we present an extension of the reservoir technique (see, [Alouges et al., Submitted; Alouges et al.(2002a), In: Finite volumes for complex applications, III, pp. 247–254, Marseille; Alouges et al.(2002b), C. R. Math. Acad. Sci. Paris, 335(7), 627–632.]) for two-dimensional advection equations with non-constant velocities. The purpose of this work is to make decrease the numerical diffusion of finite volume schemes, correcting the numerical directions of propagation, using a so-called corrector vector combined with the reservoirs. We then introduce an object called velocities rose in order to minimize the algorithmic complexity of this method.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Alouges, F., De Vuyst, F., Le Coq, G., and Lorin, E. The reservoir technique: a way to make godunov-type schemes zero or very low-diffuse. Preprint CMLA 2005-16 (In revision).
Alouges, F., De Vuyst, F., Le Coq, G., and Lorin, E. (2002). The reservoir scheme for systems of conservation laws. In Finite Volumes for Complex Applications, III (Porquerolles, 2002), pp. 247–254 (electronic). Laboratory Analytic Topology Probablity CNRS, Marseille.
Alouges F., De Vuyst F., Le Coq G., Lorin E. (2002b). Un procédé de réduction de la diffusion numérique des schémas à différence de flux d’ordre un pour les systèmes hyperboliques non linéaires. C. R. Math. Acad. Sci. Paris, 335(7):627–632
Alouges, Le Coq, F. G., and Lorin, E. (2005). Multidimensional extension of the reservoir technique. Preprint CMLA (ENS de Cachan).
Bouchut F. (2004). An antidiffusive entropy scheme for monotone scalar conservation laws. J. Sci. Comput. 21(1):1–30
Billett S.J., Toro E.F. (1997). On WAF-type schemes for multidimensional hyperbolic conservation laws. J. Comput. Phys. 130(1):1–24
Cockburn B. (2003). Discontinuous Galerkin methods. ZAMM Z. Angew. Math. Mech. 83(11):731–754
DiPerna R.J., Lions P.-L. (1989). Ordinary differential equations, transport theory and Sobolev spaces. Invent. Math. 98(3):511–547
Després B., Lagoutière F. (1999). Un schéma non linéaire anti-dissipatif pour l’équation d’advection linéaire. C. R. Acad. Sci. Paris Sér. I Math. 328(10):939–944
Després B., Lagoutière F. (2002). Contact discontinuity capturing schemes for linear advection and compressible gas dynamics. J. Sci. Comput. 16(4):479–524
de Sousa F.S., Mangiavacchi N., Nonato L.G., Castelo A., Tomé M.F., Ferreira V.G., Cuminato J.A., McKee S. (2004). A front-tracking/front-capturing method for the simulation of 3D multi-fluid flows with free surfaces. J. Comput. Phys. 198(2):469–499
Eymard, R., Gallouët, T., and Herbin, R. (2000). Finite volume methods. In Handbook of Numerical Analysis, Vol. VII, Handb. Numerical Analysis, VII. North-Holland, Amsterdam, pp. 713–1020.
Ghidaglia J.-M., Kumbaro A., Le Coq G. (1996). Une méthode “volumes finis” à flux caractéristiques pour la résolution numérique des systèmes hyperboliques de lois de conservation. C. R. Acad. Sci. Paris Sér. I Math. 322(10):981–988
Godlewski E., Raviart P.-A. (1996). Numerical Approximation of Hyperbolic Systems of Conservation laws, Applied Mathematical Sciences Vol 118. Springer-Verlag, New York
Harten, A. (1987). Preliminary results on the extension of ENO schemes to two-dimensional problems. In Nonlinear hyperbolic problems (St. Etienne, 1986) Lecture Notes in Mathematics, Vol. 1270, Springer, Berlin, pp. 23–40.
Labbé, S., and Lorin, E. On the reservoir technique convergence. Preprint CRM-3222.
Roe P.L. (1981). Approximate Riemann solvers, parameter vectors, and difference schemes. J. Comput. Phys. 43(2):357–372
Shu, C. -W. (1999). High-order ENO and WENO schemes for computational fluid dynamics. In High-order methods for computational physics, Lecture Notes Computer Science Engineering, Vol. 9, Springer, Berlin, pp. 439–582.
Xu Z., Shu C.-W. (2005). Anti-diffusive flux corrections for high-order finite WENO schemes. J. Comput. Phys. 205(2):458–485
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Alouges, F., Le Coq, G. & Lorin, E. Two-Dimensional Extension of the Reservoir Technique for Some Linear Advection Systems. J Sci Comput 31, 419–458 (2007). https://doi.org/10.1007/s10915-006-9115-7
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10915-006-9115-7