Skip to main content
SpringerLink
Log in

On the Hausdorff distance between the Heaviside step function and Verhulst logistic function

  • Original Paper
  • Published:
Journal of Mathematical Chemistry Aims and scope Submit manuscript

Abstract

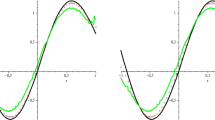
In this note we prove more precise estimates for the approximation of the step function by sigmoidal logistic functions. Numerical examples, illustrating our results are given, too.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

References

  1. R. Alt, S. Markov, Theoretical and computational studies of some bioreactor models. Comput. Math. Appl. 64, 350–360 (2012). doi:10.1016/j.camwa.2012.02.046

    Article  Google Scholar 

  2. R. Anguelov, S. Markov, Hausdorff continuous interval functions and approximations, in SCAN 2014 Proceedings, LNCS, ed. by J.W. von Gudenberg (Springer, Berlin, 2015)

    Google Scholar 

  3. R. Anguelov, S. Markov, B. Sendov, On the normed linear space of Hausdorff continuous functions, in LNSC 3743, ed. by I. Lirkov, et al. (Springer, Berlin, 2006), pp. 281–288

    Google Scholar 

  4. R. Anguelov, S. Markov, B. Sendov, The set of Hausdorff continuous functions—the largest linear space of interval functions. Reliab. Comput. 12, 337–363 (2006)

    Article  Google Scholar 

  5. I.A. Basheer, M. Hajmeer, Artificial neural networks: fundamentals, and application. J. Microbiol. Methods 43, 3–31 (2000). doi:10.1016/S0167-7012(00)00201-3

    Article  CAS  Google Scholar 

  6. A.M. Bersani, G. DellAcqua, Is there anything left to say on enzyme kinetic constants and quasi-steady state approximation? J. Math. Chem. 50, 335–344 (2012)

    Article  CAS  Google Scholar 

  7. M. Carrillo, J.M. Gonzalez, A new approach to modelling sigmoidal curves. Technol. Forecast. Soc. Change 69, 233–241 (2002). doi:10.1016/S0040-1625(01)00150-0

    Article  Google Scholar 

  8. Z. Chen, F. Cao, The approximation operators with sigmoidal functions. Comput. Math. Appl. 58, 758–765 (2009). doi:10.1016/j.camwa.2009.05.001

    Article  Google Scholar 

  9. Z. Chen, F. Cao, The construction and approximation of a class of neural networks operators with ramp functions. J. Comput. Anal. Appl. 14, 101–112 (2012)

    Google Scholar 

  10. Z. Chen, F. Cao, J. Hu, Approximation by network operators with logistic activation functions. Appl. Math. Comput. 256, 565–571 (2015). doi:10.1016/j.amc.2015.01.049

    Article  Google Scholar 

  11. D. Costarelli, R. Spigler, Approximation results for neural network operators activated by sigmoidal functions. Neural Netw. 44, 101–106 (2013). doi:10.1016/j.neunet.2013.03.015

    Article  Google Scholar 

  12. D. Costarelli, R. Spigler, Constructive approximation by superposition of sigmoidal functions. Anal. Theory Appl. 29, 169–196 (2013). doi:10.4208/ata.2013.v29.n2.8

    Google Scholar 

  13. J. Dombi, Z. Gera, The approximation of piecewise linear membership functions and Likasiewicz operators. Fuzzy Sets Syst. 154, 275–286 (2005). doi:10.1016/j.fss.2005.02.016

    Article  Google Scholar 

  14. F. Hausdorff, Set Theory, 2nd edn. (Chelsea Publ., New York, 1962 [1957]) (Republished by AMS-Chelsea 2005), ISBN: 978–0–821–83835–8

  15. A. Iliev, N. Kyurkchiev, S. Markov, On the approximation of the cut and step functions by logistic and Gompertz functions. Int. J. Math. Models Biosci. (2015, accepted)

  16. A.G. McKendrick, M. Kesava Pai, The rate of multiplication of micro-organisms: a mathematical study. Proc. R. Soc. Edinb. 31, 649–653 (1912). doi:10.1017/S0370164600025426

    Article  CAS  Google Scholar 

  17. N. Kyurkchiev, S. Markov, Sigmoidal functions: some computational and modelling aspects. Biomath Commun. 1 (2014). doi:10.11145/j.bmc.2015.03.081

  18. N. Kyurkchiev, S. Markov, Sigmoid Functions: Some Approximation and Modelling Aspects. Some Moduli in Programming Environment Mathematica (LAP Lambert Acad. Publ., Saarbrucken, 2015) ISBN: 978–3–659–76045–7

  19. S. Markov, Cell growth models using reaction schemes: batch cultivation. Biomath 2, 1312301 (2013). doi:10.11145/j.biomath.2013.12.301

    Google Scholar 

  20. M.V. Putz, A.M. Putz, Logistic vs. W-Lambert information in quantum modeling of enzyme kinetics. Int. J. Chemoinf. Chem. Eng. 1, 42–60 (2011)

    CAS  Google Scholar 

  21. N. Radchenkova, M. Kambourova, S. Vassilev, R. Alt, S. Markov, On the mathematical modelling of EPS production by a thermophilic bacterium. Biomath 3 (2014). doi:10.11145/j.biomath.2014.07.121

  22. F. Rosenblat, The perceptron: a probabilistic model for information storage and organization in the brain, Cornell aeronautical laboratory. Psychol. Rev. 65, 386–408 (1958)

    Article  Google Scholar 

  23. B. Sendov, Hausdorff Approximations (Kluwer, Boston, 1990). doi:10.1007/978-94-009-0673-0

    Book  Google Scholar 

  24. B. Sendov, V. Popov, The exact asymptotic behavior of the best approximation by algebraic and trigonometric polynomials in the Hausdorff metric. Math. Sb. (N. S.) 89, 138–147 (1972)

    Google Scholar 

  25. J. Traub, Iterative Methods for the Solution of Equations (Chelsea Publ., N. Y., 1982)

    Google Scholar 

  26. J. H. Van der Walt, The linear space of Hausdorff continuous interval functions. Biomath 2 (2013). doi:10.11145/j.biomath.2013.11.261

  27. P.-F. Verhulst, Notice Sur la Loi Que la Population Poursuit dans Son Accroissement. Corresp. Math. Phys. 10, 113–121 (1838)

    Google Scholar 

  28. P.-F. Verhulst, Recherches Mathematiques sur la Loi D’accroissement de la Population (Mathematical Researches into the Law of Population Growth Increase). Nouveaux Memoires de l’Academie Royale des Sciences et Belles-Lettres de Bruxelles 18, 1–42 (1845)

    Google Scholar 

  29. P.-F. Verhulst, Deuxieme Memoire sur la Loi D’accroissement de la Population. Memoires de l’Academie Royale des Sciences, des Lettres et des Beaux-Arts de Belgique 20, 1–32 (1847)

    Google Scholar 

Download references

Acknowledgments

The authors greatly appreciate the referee’s suggestions.

Author information

Authors and Affiliations

  1. Sofia, Bulgaria

    Nikolay Kyurkchiev & Svetoslav Markov

Authors
  1. Nikolay Kyurkchiev
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Svetoslav Markov
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Nikolay Kyurkchiev.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kyurkchiev, N., Markov, S. On the Hausdorff distance between the Heaviside step function and Verhulst logistic function. J Math Chem 54, 109–119 (2016). https://doi.org/10.1007/s10910-015-0552-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10910-015-0552-0

Keywords

Search

Navigation