Estimation of partial linear error-in-variables models for ρ⁻-mixing dependence data

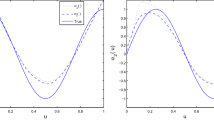
Consider the partly linear regression model Y = xβ + g(t) + e where the explanatory x is erroneously measured, and both t and the response Y are measured exactly, the random error e is ρ⁻-mixing. Let $\tilde{x}$ be a surrogate variable observed instead of the true x in the primary survey data. Assume that in addition to the primary data set containing N observations of $\big\{(Y_{j},\tilde{x}_{j},t_{j})_{j=n+1}^{n+N}\big\}$, which is ρ⁻-mixing data sets, an independent validation data containing n observations of $\big\{(x_{j},\tilde{x}_{j},t_{j})_{j=1}^{n}\big\}$ is available. The exact observations on x may be obtained by some expensive or diffcult procedures for only a small subset of subjects enrolled in the study. In this paper, inspired by Berberan-Santos et al. [J. Math. Chem. 37 (2005)101], a semiparametric method with the primary data is employed to obtain the estimators of β and g(·) based on the least squares criterion with the help of validata. The proposed estimators are proved to be strongly consistent.