1 Introduction

In recent years, with the rapid development of material production technology, the physical characteristics of low dimensional materials have aroused great interest. Especially, there has been a great deal of interest in the investigation of quantum dot. There has been a large amount of experimental work [1–6] on quantum dots. Several investigators have studied the properties of the quantum dot in many aspects by a variety of theoretical methods. For example, using compact-density matrix approach and exact analytical method, Lu et al. [7] obtained analytical expressions of the optical absorption coefficients and refractive index changes in a two-electron quantum dot with oscillating and linear confining terms. In the same year, a theoretical study of the effects of intense laser fields on the nonlinear properties of donor impurities in a quantum dot with Woods-Saxon potential is performed by them [8] within the matrix diagonalization method with the use of the effective mass approximation. Wang et al. [9] have studied the binding energy of hydrogenic impurities in a GaAs cylindrical QD by using a two-parameter variational wave function. Melnikov et al. [10] studied the properties of bound polaron in a spherical quantum dot employing the all-coupling variational approach. Manvir [11] proposed the theoretical investigation of the effect of the Rashba-type spin-orbit interaction on the Fock-Darwin energy spectrum in the parabolically confined quantum dots in the presence of a perpendicular magnetic field. Chen et al. [12] reported the quantum interference and spin accumulation on double quantum dots with Rashba spin-orbit coupling and electron interaction based on keldysh nonequilibrium Green’s function formalism. With the effective mass approximation and finite barrier potential, Sadegh and Rezaie [13] studied the effect of magnetic field on the impurity binding energy of the excited states in spherical quantum dot. Chen et al. [14] investigated the temperature dependence of the binding energy of an impurity bound magnetopolaron in a GaAs parabolic dot by using the second-order Rayleigh-Schrodinger perturbation theory. However, the properties of the polaron in an asymmetric quantum dot has not been investigated so far by employing an improved linear combination operator method. Especially, the temperature effect on effective mass of strong-coupling polaron in an asymmetric quantum dot has never been studied yet.

In this paper, we investigate the temperature effect on the mean number phonons and the effective mass of the polaron in an asymmetric quantum dot by using the improved linear combination operator method.

2 Theoretical Model

The moving of the electron in the crystal is surrounded by the other medium. Due to the phonon field and the polar crystal boundary effect, the moving of the electron in every direction is in quantization. On the assumption that the electron in the quantum dot is bounded by different parabolic potential in z direction and x–y plane, the electron-phonon system Hamiltonian in an asymmetric quantum dot can be written as

$$\begin{aligned} H&= \frac{{P^{2} }}{{2m}} + \sum \limits _{{\mathbf {k}}} {\hbar \omega _{{LO}} a_{{\mathbf {k}}}^{ + } } a_{{\mathbf {k}}} + \frac{1}{2}m\omega _{1}^{2} \rho ^{2} + \frac{1}{2}m\omega _{2}^{2} z^{2} \nonumber \\&+ \sum \limits _{{\mathbf {k}}} {[V_{\mathrm{k}} a_{{\mathbf {k}}} \exp (i{\mathbf {k}} \cdot {\mathbf {r}}) + h \cdot c]} . \end{aligned}$$
(1)

where \(m\) is the band mass, \(\omega _1 \) and \(\omega _2 \) are the transverse and longitudinal confinement strengths of the three-dimensional anisotropic harmonic potential in the x–y plane and z direction. \(a_\mathbf k ^+ (a_\mathbf k )\) denotes the creation(annihilation) operator of the LO phonons with wave vector \(\mathbf k \), and \(\mathbf r \) is the position vectors of an electron.

$$\begin{aligned} V_{\mathrm{k}} = i\left( {\frac{{\hbar \omega _{{LO}} }}{\mathrm{k}}} \right) \left( {\frac{\hbar }{{2m\omega _{{LO}} }}} \right) ^{{1/4}} \left( {\frac{{4\pi \alpha }}{V}} \right) ^{{1/2}} , \end{aligned}$$
(2)
$$\begin{aligned} \alpha = \left( {\frac{{e^{2} }}{{2\hbar \omega _{{LO}} }}} \right) \left( {\frac{{2m\omega _{{LO}} }}{\hbar }} \right) ^{{1/2}} \left( {\frac{1}{{\varepsilon _{\infty } }} - \frac{1}{{\varepsilon _{0} }}} \right) , \end{aligned}$$
(3)

Carrying out the unitary transformation to Eq. (1)

$$\begin{aligned} U=\exp \left[ \sum \limits _k {(a_k^+ f_k -a_k f_k^*)}\right] . \end{aligned}$$
(4)

Then we introduce the improved linear combination operators

$$\begin{aligned} p_{j} = \left[ {\frac{{m\hbar \lambda }}{2}} \right] ^{{1/2}} (b_{j} + b_{j}^{ + } + P_{{0j}} ), \end{aligned}$$
(5)
$$\begin{aligned} r_{j} = i\left[ {\frac{\hbar }{{2m\lambda }}} \right] ^{{1/2}} (b_{j} - b_{j}^{ + } ),j = x,y,z\;. \end{aligned}$$
(6)

where \(f_k (f_k^*)\), \(\lambda \) and \(P_0 \) are variational parameters, and \(\lambda \) expresses the vibrational frequency of the polaron. We choose the following ground state wave function of the system

$$\begin{aligned} \left| {\psi _{0} } \right\rangle = \left| 0 \right\rangle _{a} \left| 0 \right\rangle _{b} , \end{aligned}$$
(7)

\(\left| 0 \right\rangle _b \)is the vacuum state of the \(b\) operator and \(\left| 0 \right\rangle _a \)is the unperturbed zero phonon state, which satisfies \(b_j \left| 0 \right\rangle _b =a_k \left| 0 \right\rangle _a =0\). To obtain the effective mass of the strong-coupling polaron, the minimization of the energy should be performed by constraining the total momentum operator \( {\mathbf {P}}_{{{//\mathrm{T}}}} \) of the system parallel to the x–y plane. The operator can be written as

$$\begin{aligned} {\mathbf {P}}_{{{//T}}} = {\mathbf {P}}_{{{//}}} + \sum \limits _{{\mathbf {k}}} {a_{{\mathbf {k}}}^{ + } } a_{{\mathbf {k}}} \hbar {\mathbf {k}}_{{{//}}} \;. \end{aligned}$$
(8)

The expectation value of \( U^{{ - 1}} (H - {\mathbf {u}} \cdot {\mathbf {P}}_{{//{\text {T}}}} )U \)for the ground state \(\left| {\psi _0 } \right\rangle \), where \(u\) is a Lagrange multiplier, is

$$\begin{aligned} F(\lambda ,f_{k} ,u,P_{0} ) = \left\langle {\psi _{0} } \right| U^{{ - 1}} (H - {\mathbf {u}} \cdot {\mathbf {P}}_{{{//\mathrm{T}}}} )U\left| {\psi _{0} } \right\rangle \;. \end{aligned}$$
(9)

\(F(\lambda ,f_k ,u,P_0 )\) may be called the variational parameter function. Using variational method, we get \(f_k (f_k^*)\) and \(P_0 \). Taking \(f_k (f_k^*)\) and \(P_0 \) into Eq. (9), we have

$$\begin{aligned} F(\lambda ,u) = \frac{3}{4}\hbar \lambda + \frac{{\hbar \omega _{1}^{2} }}{{2\lambda }} + \frac{{\hbar \omega _{2}^{2} }}{{4\lambda }} - \frac{1}{2}mu^{2} - \frac{\alpha }{{3\sqrt{\pi }}}\left( {\frac{\lambda }{{\omega _{{LO}} }}} \right) ^{{3/2}} mu^{2} - \frac{{\alpha \hbar }}{{\sqrt{\pi }}}\sqrt{\lambda \omega _{{LO}} }.\nonumber \\ \end{aligned}$$
(10)

For the momentum expectation value, we find

$$\begin{aligned} P_{{//}} = \left\langle {\psi _{0} } \right| P_{{//T}} \left| {\psi _{0} } \right\rangle = m\left( {\frac{{2\alpha }}{{3\sqrt{\pi }}}\left( {\frac{\lambda }{{\omega _{{LO}} }}} \right) ^{{3/2}} + 1} \right) u\;. \end{aligned}$$
(11)

It is evident from the structure of this expression that \(u\) has the meaning of velocity which may be regarded as the average velocity of the polaron in the x–y plane, and the factor before \(u\),

$$\begin{aligned} m^{ * } = m\left( {\frac{{2\alpha }}{{3\sqrt{\pi }}}\left( {\frac{\lambda }{{\omega _{{LO}} }}} \right) ^{{2/3}} + 1} \right) \;. \end{aligned}$$
(12)

It can be interpreted as the effective mass of the strong-coupling polaron in an asymmetric quantum dot.

Performing the variation of \(F(\lambda ,u)\)with respect to \(\lambda \), we get the polaron’s vibrational frequency

$$\begin{aligned} \lambda ^{2} - \frac{2}{3}\alpha \sqrt{\frac{{\omega _{{LO}} }}{\pi }} \lambda ^{{3/2}} - \left( {\frac{2}{3}\omega _{1}^{2} + \frac{1}{3}\omega _{2}^{2} } \right) = 0, \end{aligned}$$
(13)

Solving Eq. (13), we get the vibrational frequency of the polaron

$$\begin{aligned} \lambda =\lambda _0 , \end{aligned}$$
(14)

Substituting \(\lambda _0 \) in Eq. (12), Choosing the usual polaron units, the vibrational frequency and the effective mass are

$$\begin{aligned} \lambda ^{2} - \frac{{2\alpha }}{{3\sqrt{\pi }}}\lambda ^{{3/2}} - \frac{1}{3}\left( {\frac{8}{{l_{1}^{4} }} + \frac{4}{{l_{2}^{4} }}} \right) = 0, \end{aligned}$$
(15)
$$\begin{aligned} m^{ * } = \frac{\alpha }{{3\sqrt{\pi }}}\lambda _{0} ^{{3/2}} + \frac{1}{2}, \end{aligned}$$
(16)

where \(l_1 =\sqrt{\frac{\hbar }{m\omega _1 }} ,l_2 =\sqrt{\frac{\hbar }{m\omega _2 }} \) are the transverse and longitudinal effective confinement lengths, respectively. The mean number of optical phonons of the ground state around the electron is

$$\begin{aligned} N = \left\langle {\psi _{0} } \right| U^{{ - 1}} \sum \limits _{{\mathbf {k}}} {a_{{\mathbf {k}}}^{ + } } a_{{\mathbf {k}}} U\left| {\psi _{0} } \right\rangle = \frac{\alpha }{{\sqrt{\pi }}}\sqrt{\lambda _{0} } . \end{aligned}$$
(17)

3 Temperature Effects

At finite temperature, the electron-phonon system is no longer entirely in the ground state. The lattice vibrations excite not only the real phonon but also the electron in a parabolic potential. The properties of the polaron are a statistical average over various states. According to the quantum statistics theory, the statistical average number of the optical phonons is

$$\begin{aligned} \bar{N}=\left[ {\exp \left( {\frac{1}{K_B T}}\right) -1} \right] ^{-1}. \end{aligned}$$
(18)

where \(K_B \) is the Boltzmann constant. However, the value of \(\lambda _0 \) in Eq. (17) relates not only to the value of \(N\) but also to the value of \(\bar{N}\), which should be self-consistently calculated with Eq. (18), and then we can obtain the relation between \(N\), \(m^*\) and \(T\).

4 Numerical Result and Discussion

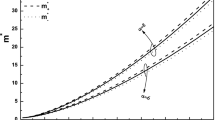
To show more obviously the influence of the temperature \(T\)on the mean number of phonons and the effective mass of the strong-coupling polaron in an asymmetric quantum dot, we perform a calculation. The results are presented in Figs. 1, 2, 3, and 4.

Fig. 1
figure 1

The relationship between the mean number phonons \(N\) and temperature \(T\)

Full size image
Fig. 2
figure 2

The relationship between effective mass m\(^*\) and temperature \(T\)at different electron-LO phonon coupling strength \(\alpha \)

Full size image
Fig. 3
figure 3

The relationship between effective mass m\(^*\) and temperature \(T\) at different transverse confinement length \(l_1 \)

Full size image
Fig. 4
figure 4

The relationship between effective mass m\(^*\) and temperature \(T\) at different longitudinal confinement length \(l_2 \)

Full size image

Figure 1 shows the relation between the temperature and the mean number phonons. From the figure, it can be seen an interesting phenomena that the change of the mean number phonons is zero near \(T=0\). When \(T>2K\), it rapidly increases with increasing the temperature.

The effective mass \(m^*\) as a function of the temperature \(T\) at different electron-phonon coupling strength \(\alpha \) is shown in Fig. 2 with \(l_1 =0.6,l_2 =0.8\) and \(\lambda =5\). Figure 3 indicates the relationship between effective mass \(m^*\) and temperature \(T\) at different transverse confinement length \(l_1 \) for fixed \(\lambda =5,l_2 =1.0\) and \(\alpha =8\). Figure 4 shows the effective mass \(m^*\) change with the temperature at different longitudinal confinement length \(l_2 \) for \(l_1 =0.6,\lambda =5\) and \(\alpha =8\). From Figs. 2, 3, and 4, we can see that the effective mass is an increasing function of the temperature. There are two reasons which make the temperature raise the effective mass of the electron. One reason is that higher temperature makes the crystal polarized much easier, the bulk phonon increases with the rising of temperature. Another reason is that the higher temperature increases the speed of heat sport of the electron and phonons. For these reasons, the electron interacts with even more bulk phonons. Hence, the mean number phonons and the effective mass of the polaron increase with the increase of temperature. We also can see that, at the same position (same value of T), the higher electron-phonon coupling strength \(\alpha \), and the smaller effective confinement strength \(l_1 ,l_2 \), the lager is the effective mass \(m^*\).

From Fig. 2, one can see that the effective mass will increase with increasing the electron-phonon coupling strength. This is because the larger the electron-phonon coupling strength is, the stronger the electron-phonon interaction is. Therefore, it makes the electron interact with more phonons. As a result, the effective mass increases with increasing electron-phonon coupling strength. From Figs. 3 and 4, we can see that the effective mass is larger with the smaller transverse and longitudinal effective confinement lengths. These can be attributed to the interesting quantum size effects. We also see that the influence of the transverse confinement length on the effective mass is larger than that of the longitudinal one.

5 Conclusion

In conclusion, based on the improved linear combination operator method, we investigate the temperature effect of the mean number phonons and the effective mass of the strong-coupling polaron in an asymmetric quantum dot. It is found that the mean number of phonons and the effective mass are increasing functions of the temperature.