Skip to main content
SpringerLink
Log in

An enhanced formulation for solving graph coloring problems with the Douglas–Rachford algorithm

  • Published:
Journal of Global Optimization Aims and scope Submit manuscript

Abstract

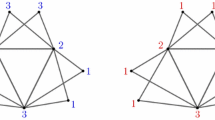
We study the behavior of the Douglas–Rachford algorithm on the graph vertex-coloring problem. Given a graph and a number of colors, the goal is to find a coloring of the vertices so that all adjacent vertex pairs have different colors. In spite of the combinatorial nature of this problem, the Douglas–Rachford algorithm was recently shown to be a successful heuristic for solving a wide variety of graph coloring instances, when the problem was cast as a feasibility problem on binary indicator variables. In this work we consider a different formulation, based on semidefinite programming. The much improved performance of the Douglas–Rachford algorithm, with this new approach, is demonstrated through various numerical experiments.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

Notes

  1. top95: http://magictour.free.fr/top95.

  2. DIMACS benchmark instances: http://cse.unl.edu/~tnguyen/npbenchmarks/graphcoloring.html.

References

  1. Achlioptas, D., Friedgut, E.: A sharp threshold for \(k\)-colorability. Random Struct. Algorithm 14, 63–70 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  2. Achlioptas, D., Molloy, M.: Almost all graphs with \(2.522n\) edges are not 3-colorable. Electron. J. Comb. 6(1), R29 (1999)

    Article  MathSciNet  Google Scholar 

  3. Aragón Artacho, F.J., Borwein, J.M., Martín-Márquez, V., Yao, L.: Applications of convex analysis within mathematics. Math. Program. Ser. B 148(1–2), 49–88 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  4. Aragón Artacho, F.J., Borwein, J.M., Tam, M.K.: Douglas–Rachford feasibility methods for matrix completion problems. ANZIAM J. 55(4), 299–326 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  5. Aragón Artacho, F.J., Borwein, J.M., Tam, M.K.: Recent results on Douglas–Rachford methods for combinatorial optimization problem. J. Optim. Theory Appl. 163(1), 1–30 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  6. Aragón Artacho, F.J., Borwein, J.M., Tam, M.K.: Global behavior of the Douglas–Rachford method for a nonconvex feasibility problem. J. Glob. Optim. 65(2), 309–327 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  7. Aragón Artacho, F.J., Campoy, R.: Solving graph coloring problems with the Douglas–Rachford algorithm. Set Valued Var. Anal. 26(2), 277–304 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  8. Baillon, J.B., Bruck, R.E., Reich, S.: On the asymptotic behavior of nonexpansive mappings and semigroups in Banach spaces. Houst. J. Math. 4(1), 1–9 (1978)

    MathSciNet  MATH  Google Scholar 

  9. Bauschke, H.H., Combettes, P.L.: Convex Analysis and Monotone Operator Theory in Hilbert Spaces, 2nd edn. Springer, Berlin (2017)

    Book  MATH  Google Scholar 

  10. Bauschke, H.H., Koch, V.R.: Projection methods: Swiss army knives for solving feasibility and best approximation problems with halfspaces. Contemp. Math. 636, 1–40 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  11. Bauschke, H.H., Noll, D.: On the local convergence of the Douglas–Rachford algorithm. Arch. Math. 102(6), 589–600 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  12. Benoist, J.: The Douglas–Rachford algorithm for the case of the sphere and the line. J. Glob. Optim. 63(2), 363–380 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  13. Cegielski, A.: Iterative methods for fixed point problems in Hilbert spaces. Lecture Notes in Mathematics, vol. 2057. Springer, Heidelberg (2012)

  14. Chaitin, G.J.: Register allocation and spilling via graph coloring. SIGPLAN Not. 39(4), 66–74 (2004)

    Article  MathSciNet  Google Scholar 

  15. Dolan, E.D., Moré, J.J.: Benchmarking optimization software with performance profiles. Math. Program. Ser. A 91(2), 201–213 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  16. Elser, V., Rankenburg, I., Thibault, P.: Searching with iterated maps. Proc. Natl. Acad. Sci. 104(2), 418–423 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  17. Erdös, P., Rényi, A.: On random graphs I. Publ. Math. Debr. 6, 290–297 (1959)

    MATH  Google Scholar 

  18. Formanowicz, P., Tanaś, K.: A survey of graph coloring—its types, methods and applications. Found. Comput. Decis. Sci. 37(3), 223–238 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  19. Garey, M.R., Johnson, D.S., So, H.C.: An application of graph coloring to printed circuit testing. IEEE Trans. Circuits Syst. 23(10), 591–599 (1976)

    Article  MathSciNet  MATH  Google Scholar 

  20. Hale, W.K.: Frequency assignment: theory and applications. Proc. IEEE 68(12), 1497–1514 (1980)

    Article  Google Scholar 

  21. Hesse, R., Luke, D.R.: Nonconvex notions of regularity and convergence of fundamental algorithms for feasibility problems. SIAM J. Optim. 23(4), 2397–2419 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  22. Horn, R.A., Johnson, C.R.: Matrix Analysis, 2nd edn. Cambridge University Press, Cambridge (2013)

    MATH  Google Scholar 

  23. Izmailov, A.F., Solodov, M.V., Uskov, E.T.: Globalizing stabilized sequential quadratic programming method by smooth primal-dual exact penalty function. J. Optim. Theory Appl. 169(1), 1–31 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  24. Jensen, T.R., Toft, B.: Graph Coloring Problems. Wiley, New York (1995)

    MATH  Google Scholar 

  25. Johansson, F: mpmath, version 1.0 (2017). http://mpmath.org

  26. Karger, D., Motwani, R., Sudan, M.: Approximate graph coloring by semidefinite programming. J. ACM (JACM) 45(2), 246–265 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  27. Karp, R.M.: Reducibility among combinatorial problems. In: Miller, R., Thatcher, J. (eds.) Complexity of Computer Computations, pp. 85–103. Plenum Press, New York (1972)

    Chapter  Google Scholar 

  28. Leighton, F.T.: A graph coloring algorithm for large scheduling problems. J. Res. Natl. Bur. Stand. 84(6), 489–506 (1979)

    Article  MathSciNet  MATH  Google Scholar 

  29. Lewis, R.M.R.: A Guide to Graph Colouring: Algorithms and Applications. Springer, New York (2016)

    Book  MATH  Google Scholar 

  30. OEIS Foundation Inc.: The on-line encyclopedia of integer sequences (2018). https://oeis.org/A088202

  31. Pardalos, P.M., Mavridou, T., Xue, J.: The graph coloring problem: a bibliographic survey. In: Du, D.-Z., Pardalos, P.M. (eds.) Handbook of Combinatorial Optimization, pp. 1077–1141. Springer, New York (1998)

    Chapter  Google Scholar 

  32. Phan, H.M.: Linear convergence of the Douglas–Rachford method for two closed sets. Optimization 65(2), 369–385 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  33. Pierra, G.: Decomposition through formalization in a product space. Math. Program. 28, 96–115 (1984)

    Article  MathSciNet  MATH  Google Scholar 

  34. Tam, M.K.: Regularity properties of non-negative sparsity sets. J. Math. Anal. Appl. 447(2), 758–777 (2017)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

This work was initiated during the BIRS workshop on Splitting Algorithms, Modern Operator Theory, and Applications, organized by Heinz Bauschke, Regina Burachik and Russell Luke in Oaxaca (Mexico), in 2017. The authors thank the organizers for an excellent meeting and bringing us together.

Author information

Authors and Affiliations

  1. Department of Mathematics, University of Alicante, Alicante, Spain

    Francisco J. Aragón Artacho & Rubén Campoy

  2. Department of Physics, Cornell University, Ithaca, NY, USA

    Veit Elser

Authors
  1. Francisco J. Aragón Artacho
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Rubén Campoy
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Veit Elser
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Francisco J. Aragón Artacho.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

F. J. Aragón Artacho and R. Campoy were partially supported by MICINN of Spain and ERDF of EU, Grants MTM2014-59179-C2-1-P and PGC2018-097960-B-C22. F. J. Aragón Artacho was supported by the Ramón y Cajal program by MINECO of Spain and ERDF of EU (RYC-2013-13327) and R. Campoy was supported by MINECO of Spain and ESF of EU (BES-2015-073360) under the program “Ayudas para contratos predoctorales para la formación de doctores 2015”.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Aragón Artacho, F.J., Campoy, R. & Elser, V. An enhanced formulation for solving graph coloring problems with the Douglas–Rachford algorithm. J Glob Optim 77, 383–403 (2020). https://doi.org/10.1007/s10898-019-00867-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10898-019-00867-x

Keywords

Mathematics Subject Classification

Search

Navigation