Skip to main content
SpringerLink
Log in

A customized branch-and-bound approach for irregular shape nesting

  • Published:
Journal of Global Optimization Aims and scope Submit manuscript

Abstract

We study the Nesting Problem, which aims to determine a configuration of a set of irregular shapes within a rectangular sheet of material of fixed width, such that no overlap among the shapes exists, and such that the length of the sheet is minimized. When both translation and rotation of the shapes are allowed, the problem can be formulated as a nonconvex quadratically constrained programming model that approximates each shape by a set of inscribed circles and enforces that circle pairs stemming from different shapes do not overlap. However, despite many recent advances in today’s global optimization solvers, solving this nonconvex model to guaranteed optimality remains extremely challenging even for the state-of-the-art codes. In this paper, we propose a customized branch-and-bound approach to address the Nesting Problem to guaranteed optimality. Our approach utilizes a novel branching scheme to deal with the reverse convex quadratic constraints in the quadratic model and incorporates a number of problem-specific algorithmic tweaks. Our computational studies on a suite of 64 benchmark instances demonstrate the customized algorithm’s effectiveness and competitiveness over the use of general-purpose global optimization solvers, including for the first time the ability to find global optimal nestings featuring five polygons under free rotation.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

Notes

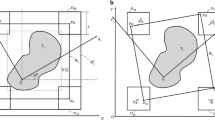
  1. In fact, one needs only impose these constraints for the vertices that constitute the convex hull of polygon \(p \in P\).

  2. For compatibility with constraints (15) and (16), the symmetry center must also be moved to point \(\left( 0,0\right) \).

  3. We prefer to use \(h_p + v_p \le h_q + v_q\), because it is likely to break symmetry in more instances.

  4. In the original implementation of Jones [14], the values 5 and 13 were proposed for parameter \(N^{\text {init}}\). However, in most instances used in this study, we found that using 5 or more circles per each and every polygon leads to initial QCP models that cannot be solved within the time limit, i.e., the GO solvers could not even complete the first (and also easiest) iteration. In contrast, using the setting \(N^{\text {init}}= 3\) and allowing the circle sets to grow more judiciously as overlaps are identified led to much better performance of the QP-Nest approach.

  5. For the sake of better numerical stability, in our implementations the width was normalized down to the value of 1, and all coordinates were scaled correspondingly.

References

  1. Achterberg, T.: SCIP: solving constraint integer programs. Math. Program. Comput. 1(1), 1–41 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  2. Alvarez-Valdes, R., Parreño, F., Tamarit, J.M.: Reactive GRASP for the strip-packing problem. Comput. Oper. Res. 35(4), 1065–1083 (2008)

    Article  MATH  Google Scholar 

  3. Alvarez-Valdes, R., Martinez, A., Tamarit, J.M.: A branch and bound algorithm for cutting and packing irregularly shaped pieces. Int. J. Prod. Econ. 145(2), 463–477 (2013)

    Article  Google Scholar 

  4. Bennell, J.A., Oliveira, J.F.: The geometry of nesting problems: a tutorial. Eur. J. Oper. Res. 184(2), 397–415 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  5. Bortfeldt, A.: A genetic algorithm for the two-dimensional strip packing problem with rectangular pieces. Eur. J. Oper. Res. 172(3), 814–837 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  6. Burke, E., Hellier, R., Kendall, G., Whitwell, G.: A new bottom-left-fill heuristic algorithm for the two-dimensional irregular packing problem. Oper. Res. 54(3), 587–601 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  7. Castillo, I., Kampas, F.J., Pintér, J.D.: Solving circle packing problems by global optimization: numerical results and industrial applications. Eur. J. Oper. Res. 191(3), 786–802 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  8. Cherri, L.H., Mundim, L.R., Andretta, M., Toledo, F.M., Oliveira, J.F., Carravilla, M.A.: Robust mixed-integer linear programming models for the irregular strip packing problem. Eur. J. Oper. Res. 253(3), 570–583 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  9. Daniels, K., Milenkovic, V.J.: Multiple translational containment: approximate and exact algorithms. In: Clarkson, K. (ed.) Proceedings of the Sixth Annual ACM-SIAM Symposium on Discrete Algorithms, pp. 205–214 (1995)

  10. Fischetti, M., Luzzi, I.: Mixed-integer programming models for nesting problems. J. Heuristics. 15(3), 201–226 (2009)

    Article  MATH  Google Scholar 

  11. Gomes, A.M., Oliveira, J.F.: Solving irregular strip packing problems by hybridising simulated annealing and linear programming. Eur. J. Oper. Res. 171(3), 811–829 (2006)

    Article  MATH  Google Scholar 

  12. Hillestad, R.J., Jacobsen, S.E.: Reverse convex programming. Appl. Math. Optim. 6, 63–78 (1980)

    Article  MathSciNet  MATH  Google Scholar 

  13. Hopper, E., Turton, B.C.: A review of the application of meta-heuristic algorithms to 2D strip packing problems. Artif. Intell. Rev. 16(4), 257–300 (2001)

    Article  MATH  Google Scholar 

  14. Jones, D.R.: A fully general, exact algorithm for nesting irregular shapes. J. Global Optim. 59, 367–404 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  15. Lindo Systems Inc.: LINDOGlobal 11.0 (2017)

  16. Milenkovic, V.J.: Rotational polygon containment and minimum enclosure using only robust 2D constructions. Comput. Geometry 13, 3–19 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  17. Misener, R., Floudas, C.A.: GloMIQO: global mixed-integer quadratic optimizer. J. Global Optim. 57(1), 3–50 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  18. Oliveira, J.F., Gomes, A.M., Ferreira, J.S.: TOPOS: a new constructive algorithm for nesting problems. OR Spektrum 22(2), 263–284 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  19. Rocha, P., Rodrigues, R., Gomes, A.M., Toledo, F.M.B., Andretta, M.: Circle covering representation for nesting problems with continuous rotations. IFAC Proc. Vol. 47(3), 5235–5240 (2014)

    Article  Google Scholar 

  20. Rodrigues, M.O., Cherri, L.H., Mundim, L.R.: MIP models for the irregular strip packing problem: new symmetry breaking constraints. ITM Web Conf. 14, 00005 (2017)

    Article  Google Scholar 

  21. Tawarmalani, M., Sahinidis, N.V.: A polyhedral branch-and-cut approach to global optimization. Math. Program. 103(2), 225–249 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  22. Wäscher, G., Haußner, H., Schumann, H.: An improved typology of cutting and packing problems. Eur. J. Oper. Res. 183(3), 1109–1130 (2007)

    Article  MATH  Google Scholar 

Download references

Acknowledgements

This work is dedicated to the memory of our academic father and grandfather, Professor Christodoulos A. Floudas. While his untimely passing has left us all with sorrow, his lasting impact on the field of Global Optimization shall remain a source of inspiration.

Author information

Authors and Affiliations

  1. Department of Chemical Engineering, Carnegie Mellon University, Pittsburgh, PA, 15213, USA

    Akang Wang, Christopher L. Hanselman & Chrysanthos E. Gounaris

Authors
  1. Akang Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Christopher L. Hanselman
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Chrysanthos E. Gounaris
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Chrysanthos E. Gounaris.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wang, A., Hanselman, C.L. & Gounaris, C.E. A customized branch-and-bound approach for irregular shape nesting. J Glob Optim 71, 935–955 (2018). https://doi.org/10.1007/s10898-018-0637-y

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10898-018-0637-y

Keywords

Search

Navigation