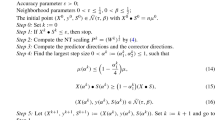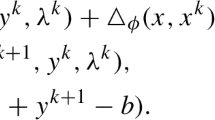Skip to main content
SpringerLink
Log in

Interior Epigraph Directions method for nonsmooth and nonconvex optimization via generalized augmented Lagrangian duality

  • Published:
Journal of Global Optimization Aims and scope Submit manuscript

Abstract

We propose and study a new method, called the Interior Epigraph Directions (IED) method, for solving constrained nonsmooth and nonconvex optimization. The IED method considers the dual problem induced by a generalized augmented Lagrangian duality scheme, and obtains the primal solution by generating a sequence of iterates in the interior of the dual epigraph. First, a deflected subgradient (DSG) direction is used to generate a linear approximation to the dual problem. Second, this linear approximation is solved using a Newton-like step. This Newton-like step is inspired by the Nonsmooth Feasible Directions Algorithm (NFDA), recently proposed by Freire and co-workers for solving unconstrained, nonsmooth convex problems. We have modified the NFDA so that it takes advantage of the special structure of the epigraph of the dual function. We prove that all the accumulation points of the primal sequence generated by the IED method are solutions of the original problem. We carry out numerical experiments by using test problems from the literature. In particular, we study several instances of the Kissing Number Problem, previously solved by various approaches such as an augmented penalty method, the DSG method, as well as several popular differentiable solvers. Our experiments show that the quality of the solutions obtained by the IED method is comparable with (and sometimes favourable over) those obtained by the differentiable solvers.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

References

  1. Bagirov, A.M., Karasözen, B., Sezer, M.: Discrete gradient method: a derivative free method for nonsmooth optimization. J. Optim. Theory Appl. 137, 317–334 (2008)

    Article  Google Scholar 

  2. Bagirov, A.M., Ganjehlou, A.N.: A quasisecant method for minimizing nonsmooth functions. Optim. Methods Softw. 25, 3–18 (2010)

    Article  Google Scholar 

  3. Burachik, R.S.: On primal convergence for augmented Lagrangian duality. Optimization 60(8–9), 979–990 (2011)

    Article  Google Scholar 

  4. Burachik, R.S., Gasimov, R.N., Ismayilova, N.A., Kaya, C.Y.: On a modified subgradient algorithm for dual problems via sharp augmented Lagrangian. J. Glob. Optim. 34, 55–78 (2006)

    Article  Google Scholar 

  5. Burachik, R.S., Iusem, A.N., Melo, J.G.: A primal dual modified subgradient algorithm with sharp Lagrangian. J. Glob. Optim. 46, 347–361 (2010)

    Article  Google Scholar 

  6. Burachik, R.S., Iusem, A.N., Melo, J.G.: Strong duality and exact penalization for general augmented Lagrangians. J. Optim. Theory Appl. 147, 125–140 (2010)

    Article  Google Scholar 

  7. Burachik, R.S., Kaya, C.Y.: An update rule and a convergence result for a penalty function method. J. Ind. Manag. Opt. 3, 381–398 (2007)

    Article  Google Scholar 

  8. Burachik, R.S., Kaya, C.Y.: An augmented penalty function method with penalty parameter updates for nonconvex optimization. Nonlinear Anal. Theory Methods Appl. 75, 1158–1167 (2012)

    Article  Google Scholar 

  9. Burachik, R.S., Kaya, C.Y.: A deflected subgradient algorithm using a general augmented Lagrangian duality with implications on penalty methods. In: Burachik, R.S., Yao, J.C. (eds.) Variational analysis and generalized differentiation in optimization and control, in honour of Boris Mordukhovich, pp. 109–132. Springer Optimization and Its Applications, New York (2010)

    Chapter  Google Scholar 

  10. Burachik, R.S., Kaya, C.Y., Mammadov, M.: An inexact modified subgradient algorithm for nonconvex optimization. Comput. Optim. Appl. 45, 1–24 (2010)

    Article  Google Scholar 

  11. Freire, W. P.: A feasible directions algorithm for convex nondifferentiable optimization. Ph.D. Thesis. COPPE/UFRJ. Rio de Janeiro. (2005) http://www.optimize.ufrj.br/files/WilhelmPassarellaFreire.pdf

  12. Gasimov, R.N.: Augmented Lagrangian duality and nondifferentiable optimization methods in nonconvex programming. J. Glob. Optim. 24, 187–203 (2002)

    Article  Google Scholar 

  13. Haarala, M., Miettinen, K., Mäkelä, M.M.: New limited memory bundle method for large-scale nonsmooth optimization. Optim. Methods Softw. 19, 673–692 (2004)

    Article  Google Scholar 

  14. Haarala, N., Miettinen, K., Mäkelä, M.M.: Globally convergent limited memory bundle method for large-scale nonsmooth optimization. Math. Program. 109, 181–205 (2007)

    Article  Google Scholar 

  15. Herskovits, J.: Feasible directions interior point technique for nonlinear optimization. J. Optim. Theory Appl. 99(1), 121–146 (1998)

    Article  Google Scholar 

  16. Herkovits, J., Freire, W.P., Tanaka, M., Canelas, A.: A feasible directions method for nonsmooth convex optimization. Struct. Multidisc. Optim. 44, 363–377 (2011)

    Article  Google Scholar 

  17. Hock, W., Schittkowski, K.: In: Test Examples for Nonlinear Programming Codes, Lecture Notes in Economics and Mathematical Systems, vol. 187. Springer, New York (1981)

  18. Kappel, F., Kuntsevich, A.V.: An implementation of Shor’s \(r\)-algorithm. Comput. Optim. Appl. 15, 193–205 (2000)

    Article  Google Scholar 

  19. Karmitsa, N., Bagirov, A., Mäkelä, M.M.: Comparing different nonsmooth minmization methods and software. Optim. Methods Softw. 47, 131–153 (2012)

    Article  Google Scholar 

  20. Karmitsa, N., Tanaka, M., Herskovits, J.: Globally convergent cutting plane method for nonconvex nonsmooth minimization. J. Optim. Theory Appl. 148, 528–549 (2011)

    Article  Google Scholar 

  21. Krejić, N., Martínez, J.M., Mello, M., Pilotta, E.A.: Validation of an augmented Lagrangian algorithm with a Gauss-Newton Hessian approximation using a set of hard-spheres problems. Comput. Optim. Appl. 16, 247–263 (2000)

    Article  Google Scholar 

  22. Lukšan, L., Vlcěk, J.: A bundle-Newton method for nonsmooth unconstrained minimization. Math. Program. 83, 373–391 (1998)

    Google Scholar 

  23. Mäkelä, M.M.: Multiobjective proximal bundle method for nonconvex nonsmooth optimization: Fortran subroutine MPBNGC 2.0, Reports of the Department of Mathematical Information Technology, Series B. Scientific Computing, B. 13/2003 University of Jyväskylä, Jyväskylä (2003)

  24. Mäkelä, M.M., Neittaanmäki, P.: Nonsmooth Optimization: Analysis and Algorithms with Applications to Optimal Control. World Scientific Publishing Co., Singapore (1992)

    Book  Google Scholar 

  25. Rockafellar, R.T., Wets, R.J.-B.: Variational Analysis. Springer, Berlin (1998)

    Book  Google Scholar 

  26. Shor, N.Z.: Minimization Methods for Non-differentiable Functions. Springer, Berlin (1985)

    Book  Google Scholar 

Download references

Acknowledgments

The authors would like to thank an anonymous reviewer for constructive remarks and queries which improved the paper. Wilhelm Freire acknowledges the inftrastructure and a motivating environment provided by the School of Mathematics and Statistics at UniSA during his one-year visit under a postdoctoral fellowship by the Brazilian government.

Author information

Authors and Affiliations

  1. School of Information Technology and Mathematical Sciences, University of South Australia, Mawson Lakes, SA, 5095, Australia

    Regina S. Burachik & C. Yalçın Kaya

  2. Federal University of Juiz de Fora, Juiz de Fora, Brazil

    Wilhelm P. Freire

Authors
  1. Regina S. Burachik
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Wilhelm P. Freire
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. C. Yalçın Kaya
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Wilhelm P. Freire.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Burachik, R.S., Freire, W.P. & Kaya, C.Y. Interior Epigraph Directions method for nonsmooth and nonconvex optimization via generalized augmented Lagrangian duality. J Glob Optim 60, 501–529 (2014). https://doi.org/10.1007/s10898-013-0108-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10898-013-0108-4

Keywords

Mathematics Subject Classification

Search

Navigation