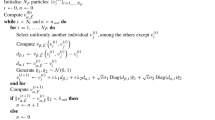Abstract
The problem of binary minimization of a quadratic functional in the configuration space is discussed. In order to increase the efficiency of the random-search algorithm it is proposed to change the energy functional by raising to a power the matrix it is based on. We demonstrate that this brings about changes of the energy surface: deep minima displace slightly in the space and become still deeper and their attraction areas grow significantly. Experiments show that this approach results in a considerable displacement of the spectrum of the sought-for minima to the area of greater depth, and the probability of finding the global minimum increases abruptly (by a factor of 103 in the case of the 10 × 10 Edwards–Anderson spin glass).
Similar content being viewed by others
References
Houdayer J., Martin O.: Hierarchical approach for computing spin glass ground states. Phys. Rev. E 64, 056704 (2001)
Hopfield J.: Neural Networks and physical systems with emergent collective computational abilities. Proc. Nat. Acad. Sci. USA 79, 2554–2558 (1982)
Hopfield J., Tank D.: Neural computation of decisions in optimization problems. Biol. Cybern. 52, 141–152 (1985)
Fu Y., Anderson P.: Application of statistical mechanics to NP-complete problems in combinatorial optimization. J. Phys. A 19, 1605–1620 (1986)
Poggio T., Girosi F.: Regularization algorithms for learning that are equivalent to multilayer networks. Science 247, 978–982 (1990)
Mulder S., Wunsch D. II: A million city traveling salesman problem solution by divide and conquer clustering and adaptive resonance neural networks. Neural Netw. 16(5–6), 827–832 (2003)
Wu F., Tam P.: A neural network methodology of quadratic optimization. Int. J. Neural Syst. 9(2), 87–93 (1999)
Pinkas G., Dechter R.: Improving connectionist energy minimization. J. Artif. Intell. Res. 3(195), 23–48 (1995)
Smith K.: Neural networks for combinatorial optimization: a review of more than a decade of research. INFORMS J. Comput. 11(1), 15–34 (1999)
Joya G., Atencia M., Sandoval F.: Hopfield neural networks for optimization: study of the different dynamics. Neurocomputing 43(1–4), 219 (2002)
Liers, F., Junger, M., Reinelt, G., Rinaldi, G.: Computing exact ground states of hard ising spin glass problems by branch-and-cut. In: Hartmann, A., Rieger, H. (eds.) New Optimization Algorithms in Physics, pp. 47–69. Wiley-VCH, Berlin (2004). http://www.informatik.uni-koeln.de/ls_juenger/research/sgs/general_info.html
Litinskii L., Magomedov B.: Global minimization of a quadratic functional: neural networks approach. Pattern Recogn. Image Anal. 15(1), 80 (2005)
Boettecher S.: Extremal optimization for Sherrington-Kirkpatrick Spin glasses. Eur. Phys. J. B 46, 501–505 (2005)
Kryzhanovskii B., Magomedov B., Mikaelyan A.: A Relation Between the Depth of a Local Minimum and the Probability of Its Detection in the Generalized Hopfield Model. Doklady Math. 72(3), 986–990 (2005)
Kryzhanovskii B., Magomedov B.: Application of domain neural network to optimization tasks. Lect. Notes Comput. Sci. 3697(II), 397 (2005)
Kryzhanovsky B., Kryzhanovsky V.: The shape of a local minimum and the probability of its detection in random search. Lect. Notes Electr. Eng. 24, 51–61 (2009)
Hartmann, A., Rieger, H. (eds.): New Optimization Algorithms in Physics. Wiley-VCH, Berlin (2004)
Duch, W., Korczak, J.: Optimization and global minimization methods suitable for neural networks. Neural Comput. Surv. 3697(II), 163–212 (1998). http://www.is.umk.pl/~duch/cv/papall.html
Hartmann, A., Rieger, H. (eds.): Optimization Algorithms in Physics. Wiley-VCH, Berlin (2001)
Karandashev Y., Kryzhanovsky B.: Transformation of energy landscape in the problem of binary minimization. Doklady Math. 80(3), 927–931 (2009)
Kryzhanovsky B.: Expansion of a matrix in terms of external products of configuration vectors. Opt. Memory Neural Netw. 17(1), 62–68 (2008)
Amit D., Gutfreund H., Sompolinsky H.: Spin-glass models of neural networks. Phys. Rev. A 32, 1007–1018 (1985)
Kernighan B., Lin S.: An efficient heuristic procedure for partitioning graphs. Bell Syst. Technol. J. 49, 291–307 (1970)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Karandashev, I., Kryzhanovsky, B. Increasing the attraction area of the global minimum in the binary optimization problem. J Glob Optim 56, 1167–1185 (2013). https://doi.org/10.1007/s10898-012-9947-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10898-012-9947-7