Abstract
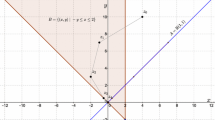
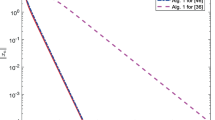
This paper develops a new variant of the classical alternating projection method for solving convex feasibility problems where the constraints are given by the intersection of two convex cones in a Hilbert space. An extension to the feasibility problem for the intersection of two convex sets is presented as well. It is shown that one can solve such problems in a finite number of steps and an explicit upper bound for the required number of steps is obtained. As an application, we propose a new finite steps algorithm for linear programming with linear matrix inequality constraints. This solution is computed by solving a sequence of a matrix eigenvalue decompositions. Moreover, the proposed procedure takes advantage of the structure of the problem. In particular, it is well adapted for problems with several small size constraints.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Bauschke H.H., Borwein J.M. (1996) On projection algorithms for solving convex feasibility problems. SIAM Rev. 38(3): 367–426
Boyd S., El Ghaoui L., Feron E., Balakrishnan V. (1994) Linear Matrix Inequalities in Systems and Control Theory. SIAM Studies in Applied Mathematics. SIAM, Philadelphia
Berman L.M. (1973) Cones, Matrices and Mathematical Programming Lecture. Notes in Economics and Mathematical Systems, vol. 79. Springer, Berlin
Bregman L.M. (1965) The method of successive projection for finding a common point of convex sets. Soviet Math. Doklay 6(3): 688–692
Gahinet P., Nemirovski A. (1997) The projective method for solving linear matrix inequalities. Math. Program. 77, 163–190
Gubin L.G., Polyak B.T., Raik E.V. (1967) The method of projections for finding the common point of convex sets. USSR Comput. Math. Math. Phys. 7(6): 1–24
Karmarkar N. (1984) A new polynomial-time algorithm for linear programming. Combinatorica 4, 373–395
Han S.P. (1988) A successive projection method. Math. Program. 40, 1–14
Luenberger D.G. (1969) Optimization by Vector Space Methods. Wiley, New York
Nesterov Yu., Nemerovski A. (1994) Interior Polynomial Point Methods in Convex Programming, SIAM Studies in Applied Mathematics. SIAM, Philadelphia
Orsi, R., Ait Rami, M., Moore, J.B.: A finite step projective algorithm for solving linear matrix inequalities. In: Proceedings of the 42nd Conference on Decision and Control, Maui, Hawaii, USA, pp. 4979–4984 (2003)
Ramana M.V. (1997) An exact duality theory for semidefinite programming and its complexity implications. Math. Program. 77, 129–162
Skelton R., Iwasaki T., Grigoriadis K. (1997) A unified algebraic approach to linear control design. Taylor & Francis, London
Sturm J. (1999) Using SeDuMi 1.02, a MATLAB toolbox for optimization over symmetric cones. Optim. Methods Software 11–12, 625–653
Vandenberghe L., Boyd S. (1996) Semidefinite programming. SIAM Rev. 38(1): 49–95
Von Neumann, J.: Functional Operators, vol. II. Princeton University Press, Princeton, NJ (1950) (this is a reprint of mineographed lecture notes distributed in 1933)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Rami, M.A., Helmke, U. & Moore, J.B. A finite steps algorithm for solving convex feasibility problems. J Glob Optim 38, 143–160 (2007). https://doi.org/10.1007/s10898-006-9088-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10898-006-9088-y