Abstract
We review progress made on the advanced tokamak path to fusion energy by the DIII-D National Fusion Facility (Luxon et al. in Nucl Fusion 42:614, 2002). The advanced tokamak represents a highly attractive approach for a future steady state fusion power plant. In this concept, there is a natural alignment between high pressure operation, favorable stability and transport properties, and a highly self-driven (‘bootstrap’) plasma current to sustain operation efficiently and without disruptions. Research on DIII-D has identified several promising plasma configurations for fully non-inductive operation with potential applications to a range of future devices, from ITER to nuclear science facilities, to compact or large scale fusion power plants. Significant progress has been made toward realizing these scenarios, with the demonstration of high β access, off-axis current drive techniques, model based profile control, and stability and ELM control in reactor relevant physics regimes. Radiative techniques have also been pioneered to develop improved compatibility with divertor requirements, and simultaneous access to high performance pedestals. Research has also developed major advances in physics understanding, validating concepts of kinetic damping of ideal MHD instabilities that enable high β operation, identifying how current profile and β influence plasma turbulence in order to validate and improve turbulent transport models, and understanding the physics of energetic particle redistribution due to Alfvénic and other instabilities. These advances have been partnered with development of a rigorous integrated modeling framework used to interpret and validate individual physics models of the various aspects of plasma behavior, and to guide development of improved regimes and upgrades. These tools are also being used to develop and validate concepts for future reactors directly. Having established these foundations, DIII-D is now undergoing a substantial upgrade to raise power, current drive, electron heating and 3-D field capabilities in order to validate this physics and test conceptual solutions in reactor-relevant physics regimes, with a goal to resolve the key scientific and technology questions to enable a decision on a future steady state fusion power plant.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction: The Advanced Tokamak Approach
The development of fusion energy represents one of the grand scientific and technological challenges of our era. Fusion offers the potential of virtually limitless energy without significant emission of greenhouse gases. This could transform human development, addressing poverty, mitigating climate change, and alleviating regional conflict. But fusion is a great technical challenge. A fusion reactor requires ions to collide at high rates and high energies to make energy in significant quantities. The frontrunner concept to achieve this is the tokamak [1, 2], which uses a principally toroidal magnetic field to confine a thermal plasma at the required densities and temperatures. Through an additional poloidal field generated by a toroidal current in the plasma, ions become confined to flux ‘surfaces’ with small scale turbulent eddies causing only low levels of thermal conduction, thereby maintaining the hot fusing core. With D-T fuel, the resulting α particles are expected to deposit energy in the plasma to maintain its temperature, while neutrons will collide with lithium in a blanket outside the plasma in order to breed the tritium fuel.
The basic principles of this plasma confinement have been demonstrated through an enormous body of research worldwide [3], enabling a decision to proceed to the reactor scale with the ITER device, which is now more than 50% constructed under a global international partnership. ITER will prove that large scale fusion approaching the Gigawatt level is possible with sufficient energy confinement for α heating effects to sustain the high plasma temperatures required. Nevertheless, the challenges to extend this concept to continuous operation in a power plant are considerable. Not only must the plasma be self-heated, it must be sustained fully non-inductively, without excessive need for auxiliary systems that may otherwise consume the energy produced, further driving up required device scale and technical challenge. Techniques to manage the high heat fluxes, and avoid transient loads, without materials erosion must be developed. And the required technologies (such as nuclear hard materials, current drive tools, tritium breeding) must be resolved.
The Advanced Tokamak (‘AT’) concept [4,5,6,7,8,9,10] provides one of the most promising approaches to meet the challenge of sustained fusion performance. The essence of the approach is to modify the plasma configuration to obtain favorable confinement and stability properties, consistent with discharge sustainment. A key aspect of this is to replace inductive current with a combination of ‘bootstrap’ current [11], naturally arising from orbit effects at high pressure gradients, and auxiliary current drive such as from radiofrequency heating [12]. The concept exploits natural synergies that emerge between plasma stability, turbulence and the current and pressure profiles that are associated with fully or highly non-inductive operation. Because of this synergy, the AT is being seen as the primary or first path to fusion energy amongst international partners engaged in the fusion endeavor, driving reactor concepts and associated scientific and engineering programs in each. Not least it is the approach for ITER’s steady state research toward fusion energy [13]. In Europe this serves as the basis on which various DEMO facilities are proposed to bridge the gap to commercial Fusion Power Plant (FPP) [14]. Options include the large EU-DEMO baseline with high recirculating power [15] and the more advanced ‘stepladder’ approach [16, 17] with longer pulse length and more optimism in technology and physics assumptions. Japan proposes a more advanced SlimCS device [18], while South Korea targets its KSTAR program on the K-DEMO device [19, 20]. In the United States, the original ARIES design [9] has been updated with various ‘Advanced and Conservative Tokamak’ (ACT) versions [21], while proposals are also made for more compact lower power designs with ARC [22] and ST Pilot Plant [23] facilities. In addition, the AT forms the basis for various proposed fusion nuclear science testing facilities such as the Fusion Development Facility (FDF) [24] and Fusion Nuclear Science Facility (FNSF) [25,26,27] in the United States, and the China Fusion Engineering Test Reactor (CFETR) [28].
All these devices, though to a lesser degree, EU-DEMO, take advantage of the basic concept of utilizing high levels of bootstrap current (from ~ 50% to as high as ~ 90%) and non-inductive current drive to sustain the plasma indefinitely (‘steady state’) or for long periods. However, as set out in Table 1, power plant concepts adopt varying levels of optimism about what can be achieved in terms of plasma regime and parameters, the engineering challenge, mission ambition, and the funding availability. Indeed, there are considerable trade-offs between these with, for instance, more optimistic assumptions about plasma performance or current drive efficiency (e.g. SlimCS, ARIES-ACT1) enabling more compact designs with lower recirculating power. Equally concerns over heat and neutron load can drive up device size unless good material and divertor solutions can be found. One can consider backing off physics demands with pulsed operation (e.g. EU-DEMO [15]), though this can increase required device size to cope with thermal cycling. Nevertheless, these concepts share the same underlying physics and technology challenges (with varying degrees of demand), and have similar considerations governing their optimization and trade-offs in mission and parameters.
Criteria for Steady State Fusion and Key Metrics
The challenge for a tokamak steady state reactor is to have sufficient fusion performance to generate net energy, after powering auxiliary systems to sustain the regime non-inductively. Following the approach of [8] we discuss the parameters that matter in developing this solution, and the associated research questions that must be explored to determine whether such a solution will be possible in a reactor.
To sustain net electric performance, a reactor must generate high fusion performance, Pfus, relative to any required auxiliary heating and current drive power, Paux, i.e., high Q = Pfus/Paux. This auxiliary power is required to meet two needs—overcoming loss power from energy transport and radiative processes, Ploss, to maintain plasma temperature, and to maintain plasma current (PCD). The plasma heating may come from fusion alpha self-heating, Pα ~ Pfus/5 in a D-T device, and from any auxiliary current drive applied, which will also heat the plasma. However, if these prove insufficient (for example, if energy confinement is too low) additional auxiliary heating will be required, Padditional heating, to balance the power lost from the plasma due to transport. Thus,
where Paux= PCD+ Padditional heating. The required plasma performance to meet this condition can be characterized in terms of an energy confinement timescale as:
In the numerator, fusion power scales with volume and the square of plasma pressure, p (provided one is in the regime where fusion cross section rises with the square of temperature, 8–25 kV). In the denominator heating power is re-expressed in terms of the characteristic energy confinement timescale \(\tau = \left\langle p \right\rangle V/P_{aux}\). Thus one arises at the familiar fusion triple product with \(Q \propto nT\tau\).
This can be expressed in terms of principle known dependencies observed in tokamak physics, to identify the important parameters governing performance. Thus pressure is expressed in terms of normalized β, given in terms of plasma current in MA, I, toroidal field, B, and minor radius, a,
This quantity characterizes stability limits that are to zeroth order independent of plasma scale parameters. Similarly, energy confinement, \(\tau ,\) can be written in terms of a multiplier of a confinement scaling, \(\tau = H\tau_{scaling}\), where \(\tau_{scaling}\) is generally found proportional current. Further, the plasma current itself can be written in terms of an edge safety factor, \(q_{95} \propto a^{2} B/RI\), which is considered to be limited by stability considerations to be > 2–3 (or higher depending on the nature and virulence of the instabilities concerned). Thus one can write:
where \(f_{Q}\) is a residual scaling that incorporates engineering variables and geometry.
From these relations, one sees immediately that device scale, a, and field, B, play critical roles in driving the fusion triple product. Substituting for Paux in (2), one arrives at:
Thus sufficient field and size can raise Q to the point that no additional heating is required beyond that needed for current drive, which we discuss shortly. However, given limits in device field and scale, one sees that the fusion performance metric, \(G = \beta_{N} H/q_{95}^{2}\) becomes important. Thus higher \(\beta_{N}\), increased confinement scaling factor, H, and particularly lower \(q_{95}\) are levering to performance and heating needs. Also, it should be noted that fusion performance can reach a point that additional heating, offers no benefit to the thermal sustainment, as the plasma ignites (reaches \(Q = \infty\)) or the current drive power alone is enough to maintain energy.
Turning to sustainment of the plasma current, two contributions are considered, again following [8]. At high βP, strong pressure gradients drive poloidal ‘banana’ currents though the overlap of ion orbits, which collisionally transfer into a net toroidal bootstrap current [11]. These ‘bootstrap’ effects contribute a fraction, fBS, to the total plasma current which scales with pressure and inversely with strength of the poloidal field:
Additional auxiliary current drive can be supplied through radiofrequency heating coupling to current carriers. This requires a population of current carriers with velocity close to the wave phase velocity, and low collisionality as collisions scatter the current carriers [29]. This generally favors plasmas with higher thermal velocities and lower density, thus:
One can rearrange these, noting \(f_{BS} + f_{CD} = 1\), to obtain the required current drive power,
If one assumes auxiliary systems are only needed for current drive (i.e., \(P_{additional -heating} = 0\)), and noting \(P_{fus} \propto \left\langle p \right\rangle^{2} R^{3} \propto \beta_{N}^{2} I^{2} B^{2} R^{3}\), then one obtains:
where density is now written in terms of fraction, fG, of a density limit parameter that scales with current, a commonly quoted empirical relation in the community, although still subject to debate.
This formalism identifies the key governing plasma physics parameters. The most critical role is played by plasma pressure, as represented by the parameter \(\beta_{N}\). This drives bootstrap fraction, thereby reducing auxiliary current drive needs. It also raises the fusion performance metric, G. High \(\beta_{N}\) thus favors steady state performance as well as fusion gain, and thus represents a key metric to improve the tokamak concept for steady state fusion. Similarly higher field provides the other means to raise pressure (at fixed \(\beta_{N}\)) and achieve ubiquitous benefits to performance and steady state goals. This strongly motivates science and technology programs to raise \(\beta_{N}\) and field respectively to optimize the tokamak concept. For the purposes of this paper we concentrate on the plasma physics aspects—how to make best use of the toroidal field available, considering progress in the underlying physics understanding of this question. We leave technology development such as higher field superconductors to other studies, though their leverage on these issues make them important to pursue also.
The second key consideration is the role of \(q_{95}\). Higher \(q_{95}\) favors higher bootstrap operation, reducing heating and current drive needs. But it also lowers fusion performance, as plasma current is lower. Conversely, a lower \(q_{95}\) will raise the fusion power, but will also require more power to be recycled back into current drive systems to sustain the device. Further, lower \(q_{95}\) increases device risk, as plasma instabilities become more severe with the increased free energy provided by the current profile, leading to disruptions (Fig. 1, left) at low \(q_{95}\) values, but absent at high \(q_{95}\). Thus the choice of \(q_{95}\) requires careful investigation in arriving at optimum reactor efficiency and in the development of robust stability and control strategies. Interestingly, it is found that disruptivity does not depend significantly on \(\beta_{N}\) (Fig. 1, right); current rather than pressure provides a much greater drive of instability in the tokamak concept. Some scenarios, such as high li or standard H modes, are more at risk of certain instabilities such as tearing modes, though at high \(q_{95}\) these tend to act on confinement rather that causing a termination.

Adapted from data in [25]
Disruptivity in the plasma current flat top period on DIII-D is found to be independent of βN but falls to zero at q95 ~ 6. Binned database of 6000 discharges spanning high qmin, high βP, high li and standard H mode discharges. (Statistical error shown in yellow).
The third key consideration is density. Lower density permits more efficient current drive. But higher density is more highly levering for bootstrap current (not discussed in above formalism, but outlined in ref [30]), as increased density gradients directly drive increased bootstrap current (provided collisionality remains low), whereas increased temperature gradient alters particle orbits in ways that can offset the benefits of increased velocity gradient. Considering the role of current profile, this divides the approach between two optimization paths—a high bootstrap solution in which auxiliary current drive needs are minimized, or efficient auxiliary current drive solution at lower density. For the driven current solution, current drive is most efficient in the hottest region of the plasma—the core. This favors a peaked current profile together with low density. This peaked current solution can access high ideal MHD stability, with high \(\beta_{N}\). However, lower density will make compatibility with a divertor solution, which favors higher density radiative techniques, more challenging.
A high bootstrap solution favors a broader current profile and elevated density. Further a broader current profiles also creates higher local \(\beta_{P}\) increasing bootstrap current. Also, the bootstrap current, as it is driven by pressure gradients, forms off-axis, thereby aligning self-consistently with a broad overall current profile. This broad current profile also benefits from a high ideal MHD \(\beta_{N}\) limit thanks to a stabilizing interaction with the surrounding conducting structure of the vessel, thereby self-consistently enabling a high bootstrap solution.
In the high bootstrap approach there is also a balance between \(q_{95}\) and \(\beta_{N}\); a higher current with lower \(q_{95}\) requires higher \(\beta_{N}\) to reach the same bootstrap fraction. The DIII-D program targets plasmas with \(\beta_{N}\) approaching 5 and \(q_{95} \sim5 - 7\) for power plant relevant scenarios, such as those set out in Table 1, which are predicted to reach very high bootstrap fractions in some cases. (We also explore alternate paths at higher \(q_{95}\) and \(\beta_{P}\), or indeed lower bootstrap fraction, for other concepts). However, plasmas that match this in DIII-D are projected to reach a lower bootstrap fraction than equivalent regimes in fusion reactors, due in part to the higher fast ion content from beams (which may ultimately be reduced by increases in other current drive systems), and the slightly more collisional plasmas attainable with the lower field and size of DIII-D. Typically DIII-D has achieved bootstrap fractions of ~ 50–60% to date in such regimes with \(\beta_{N}\) approaching 4 in fully non-inductive regimes, though higher transiently or at higher \(q_{95}\). See [31] for a more in depth discussion of the trade offs identified.
As noted in Eq. (9), confinement factor, H, does not enter into the steady state aspect of the optimization. Nevertheless transport remains important for two key reasons. Firstly, it determines the evolution of the profiles which govern bootstrap generation and stability in steady state solutions. Secondly, as one seeks to optimize the AT concept, particularly to smaller device size, sufficiently good confinement is needed to ensure α heating maintains plasma temperatures—otherwise additional auxiliary heating will be necessary, driving up required size or current to raise the fusion performance in order to power such systems.
Reviewing these considerations one can set some targets:
-
1.
It is clear from the reactor studies in Table 1, that high \(\beta_{N}\) levers a high bootstrap fraction, and this enables a reduction in device size (SlimCS) and/or current drive (ARIES-ACT1), which in turn reduces required fusion power per MW of electricity produced. It is thus clear that \(\beta_{N}\) in the range 4–5 or higher is highly desirable.
-
2.
These devices also rest on quite optimistic assumptions of current drive efficiency, typically γCD ~ 0.4 or higher for conversion of electrical power into current drive power in the higher performing designs.
-
3.
The choice of \(q_{95}\) is more complex; for reasons of disruptivity it is desirable to keep this high, ~ 5–6, though optimization of stability control may permit a lower value. For a compact lower net electric device, where α heating is more limited, this throws the focus onto confinement to ensure additional heating is not needed to sustain plasma energy. H factors have been set as high as 1.8 for ARC; it remains to be seen if this is consistent with transport physics and can be met in an integrated solution.
-
4.
The challenge in density depends somewhat on how effective a divertor solution can be developed. Thus the goal is to maximize the limits for high density radiative mantle operation (and develop a projectable physics basis for this) compatible with various core configurations possible. Note the peaked versus broad current profile paths discussed above have different optimizations.
We next consider how to get there.
Research Challenges to Enable Steady State Fusion
The advanced tokamak approach represents a natural synergy of favorable plasma physics phenomena that have the potential to lead to a self-consistent and efficient steady state solution for future energy. Section "Criteria for Steady State Fusion and Key Metrics" identifies a number of key metrics to be addressed to optimize the design of a fusion reactor. We now consider from a physics perspective what the issues are in reaching this optimization, and the questions that needed to be addressed.
The most levering parameter for a steady state tokamak of given field is \(\beta_{N}\). The principle limit to this parameter arises from ideal MHD, manifesting as a global pressure driven kink instability, constrained within profiles dictated by a soft ballooning limit. These constraints lead to a pressure limit proportional to current and field [32, 33], which is expressed as a simple number in the definition of \(\beta_{N}\) (Eq. 3). With broad current profiles, this limit is ameliorated by a dissipative interaction with the plasma wall, which can suppress the instability growth if the plasma rotates, or slows the growth rate of the instability (should it stop rotating) to the characteristic flux penetration timescale of the resistive wall, enabling magnetic feedback control of the mode. With peaked current profiles a high ‘no-wall’ ideal MHD stability limit occurs. We discuss these, and the research challenges they pose in turn.
With broad profiles, the Advanced Tokamak benefits from a strong synergy of plasma shaping and broad current and pressure distribution that assists the wall stabilization of this ideal MHD instability [34 and references therein, 7]. Firstly, plasma shaping increases current carrying capacity through volume (increased elongation) and by placing more of the plasma in high field regions (increased triangularity). This also modifies the eigenstructure of the mode to strengthen harmonics that extend more strongly beyond the plasma. This amplifies effects of a broader current profile where effectively the current perturbations associated with the mode are closer to the wall, again pushing the eigenstructure further into the wall, leading to a stronger than additive benefit of shaping and current profile. Further, a broad pressure profile moves the strongest pressure gradient to the stronger magnetic shear regions further out. Finally, as higher \(\beta_{N}\) are accessed this increases Shafranov shift which pushes the mode further out and increases local magnetic shear. The net effect is a non-linear improvement in pressure limit by up to a factor of 5 (calculated in terms of 〈 p2〉 which relates to a factor 25 in fusion performance) as summarized in Fig. 2, presented in terms of β. These considerations also naturally align with the effects and location of strong bootstrap generation.

Adapted from data in [34]
Calculated ideal MHD stability limits with strong and no shaping for broad current profiles.
On DIII-D an effective wall distance of ~ 40% of minor radius is enough to provide significant stabilization; reactor studies such as ARIES have found sufficient stability for high \(\beta_{N}\) with placement of a conducting shell distance of about 30–33% of minor radius. This opens up a window to so-called wall-stabilized operation (see Fig. 3). Access to this regime rests on development of advanced magnetic feedback tools (which must be made compatible with a reactor using advanced control physics to enable their placement outside the vessel), or exploitation of stabilizing kinetic resonances, that arise through various rotational resonances and energetic particle interactions. Understanding these interactions and developing these tools represents a major challenge that has been explored in recent years, yielding key insights and validation of the role of these kinetic resonances, and the development of advanced “state-space” controllers, discussed in this "Stability" section.
Calculated ideal MHD stability limits with and without a wall for various current profile shapes in DIII-D [based on Ref. 67]
The broad current profile also opens the door to interactions with energetic particle through the formation of resonance at weak points in the magnetic shear—so called Reverse Shear Alfvén Eigenmodes (RSAE). Understanding the stability of these modes, and the associated transport has been an area of strong progress discussed in section "Energetic Particle Physics" based on understanding thresholds for energetic particle transport, how to avoid them, and how the plasma profile can be adjusted to move weak points in the magnetic shear away from the driving energetic particle gradients.
Turning to the peaked current profile path the stability challenges differ. Peaked current profiles will include low order rational safety factor surfaces such as q = 1.5 and 2, which can be avoided with broader profiles. These are often associated with tearing instabilities and reconnection events, and require work both to predict their behavior and develop control. With the higher driven current of such scenarios, development of efficient and reactor compatible current drive tools, and the validation current drive models, becomes an important issue. (Indeed, this technology turns out to also be highly levering for the broad profile approach, where despite the high bootstrap fraction, it can still help reduce recirculating power—even high fbs reactor concepts cited in 1.1 still require quite high current drive efficiency). Work in recent years has helped test some of the key current drive physics (section "Validation of Current Drive Models"), though considerable further work is needed to develop the increased efficiencies and reactor compatibility necessary.
For both configurations, confinement in a reactor must be sufficient to avoid the need for additional heating beyond the needs of current drive. This is a particular issue for more compact or lower fusion power facilities, as the alpha heating can be more marginal relative to that required to overcome transport and radiative losses. Fortunately, both strongly positive and reverse shear are expected to be highly stabilizing to turbulence (e.g. Fig. 4 [35]). Research in recent years has focused on characterizing this relationship in relevant electron heated and low rotation regimes to aid the development of predictive transport models ("Turbulent Transport in High β Scenarios" section).

Adapted from data in [35]
Predicted transport (GYRO) versus magnetic shear at the q = 2 surface for typical DIII-D parameters.
Finally the steady state core must be made compatible with a divertor solution that prevents erosion of materials surfaces (most likely detached divertor operation). While divertor design lies outside the scope of this review, and a major research topic in its own right, the challenge must be ameliorated by radiative techniques. Understanding how these interact with the core and the tokamak pedestal is a highly salient part of the steady state scenario development, which we discuss in detail in section "Radiative Divertor Progress in Advanced Tokamak Plasmas". Compatibility with transient heat loads from Edge Localized Modes and their required control techniques are also discussed in section "Steady State Hybrid with RMP-ELM Suppression".
Having identified the physics challenges underlying the steady state scenario development, it is also important to understand how the physics comes together to develop and understand integrated steady state scenario design. Not least this is necessary to validate the basic approach described in Sects. “Criteria for Steady State Fusion and Key Metrics” and “Research Challenges to Enable Steady State Fusion”—can it be done? In practice, these scenarios also provide the workhorses to explore and test the underlying physics and control approaches. We discuss these next, laying out the approaches for scenario development on DIII-D in section "The DIII-D Approach" with various plasma operating scenarios, and the simulation tools used to guide this development. An overview of progress in each scenario is then discussed in section "Progress in the Development of Candidate Steady State Operating Scenarios", which helps clarify further the context for physics challenges, the progress on which is then discussed in section "Advances in Underlying Physics". In section "Future Research Requirements and DIII-D’s Role", we discuss plans for the facility as it goes into an exciting series of upgrades to increase current drive and heating capabilities to explore reactor like advanced scenarios with βN up to ~ 5, and develop compatibility with and techniques for a detached divertor solution. We draw out conclusions in section "Conclusions".
The DIII-D Approach
A key mission of the DIII-D program is to develop the physics basis for fully noninductive steady-state operation at high normalized β. This work is strongly motivated by the anticipated improvements in reactor economy and reliability to be gained through operation in steady state and the increase in fusion gain with βN. DIII-D has a unique capability to develop a range of steady state scenarios as a result of its flexible heating and current drive systems, strong shaping capability, feedback control system, and 3D coils for error field and resistive wall mode control. Multiple scenario options are studied because each have strengths and weaknesses. Furthermore, possible future steady state tokamak reactors (e.g. ITER, nuclear science facilities like FNSF [25, 26] or CFETR [36], DEMOs [21]) constitute a wide range of required parameters (e.g. βN from ~ 2.5 to ~ 6). Ongoing research seeks to determine which scenarios are the best choices for each device.
Range of Plasma Scenarios Explored
In recent years DIII-D has pursued four classes of steady-state scenario usually distinguished by current and safety factor profile: (1) High-βP, (2) High-qmin, (3) High-β Hybrid, and (4) High-li. These scenarios represent points on a continuum of discharge parameters, but it is helpful to understand the differences in behavior of these four points. Example profiles are shown in Fig. 5.
High-βP scenario discharges on DIII-D typically have qmin = 2–5, with q95= 10–12 [37]. The current density profile is very broad and dominated by bootstrap current (fBS = IBS/ITOTAL > 70%). Elevated qmin means low-order rational surfaces that are prone to tearing mode instability are absent from the plasma. Normalized confinement typically exceeds confinement-scaling predictions due to the presence of a high radius internal transport barrier in density, temperature, and sometimes rotation. This scenario has been studied in DIII-D in preparation for long pulse operation in the EAST tokamak [38] and is in the parameter regime envisioned for a high BT DEMO such as ACT2 [21].
High-qmin scenario discharges typically have qmin = 1.4–2.3, with q95 = 5–7 [39,40,41]. The current profile is also broad, but not as much as the High-βP scenario. Bootstrap current fraction is typically less than 65%. There is usually weak positive to negative magnetic shear (q0–qmin < 0.5) designed to reduce turbulent heat transport [42], but internal transport barriers are avoided to ensure a broad pressure profile for high ideal MHD βN-limits in the range of 4–5, depending on the detailed current profile and plasma boundary shapes. When βN exceeds the no-wall kink mode limit, the resistive wall mode becomes a potential concern [43]. This scenario is being developed as a primary option for a medium BT DEMO such as ACT1 [21], and may also be the basis for steady state operation in ITER and nuclear science facilities.
The High-β Hybrid scenario operates at lower qmin just above 1, also with q95= 5–7 [44, 45]. About half of the total current is bootstrap, and half is from on-axis external current drive using NBI and ECCD. Predicted ideal-wall βN limits of hybrid plasmas are in the range of 4–5, potentially making the highest βN applications a little more challenging. Stability to low-order tearing modes (e.g. m/n = 2/1) is improved compared to standard H-mode plasmas by the absence of sawteeth and a current profile that is somewhat broader than is predicted by resistive poloidal flux diffusion. Anomalous current profile broadening is thought to be due to the presence of 4/3 or 3/2 tearing modes that convert toroidal magnetic flux to poloidal magnetic flux [46, 47]. As a result, precise external current drive alignment to tailor the current profile is unnecessary, and external current drive can be deposited near the magnetic axis where it is most efficient. Hybrids may also be a viable operating scenario for a range of future steady state devices, depending on how the anomalous current diffusion scales to a reactor, and on how confinement is affected by increased 3/2 island width going to low rotation.
The High-li (li = internal inductance) scenario consists of a strongly peaked current density profile, with li ≈ 1 and qmin ≈ 1 [48]. At high-li, the no-wall kink-mode βN limit can be 4 or even higher; therefore the key advantage of this scenario is that it can run at high βN without reliance on wall stabilization of modes with n > 0. Strong positive magnetic shear results in high normalized confinement [42]. Like the hybrid, bootstrap current fraction is typically ~ 50%. To sustain high-li non-inductively, the current profile must be carefully controlled using significant external current drive in the inner half-radius while limiting bootstrap current in the outer half radius. For DIII-D, projections also aim to tailor the current profile to avoid sawtooth instabilities (which can trigger other instabilities), while maintaining the good core confinement benefits from high magnetic shear by avoiding too high a pedestal and edge bootstrap current. The high-li scenario is a key alternative to the other steady state scenarios for future reactors if RWM stabilization proves to be impracticable.
Considering these scenarios, we see they pose some common and some different research needs. Common element include understanding transport, energetic particle and stability physics, as well as current profile evolution in the quest to develop self-consistent steady state solutions. These issue must be understood in plasma configurations where the underlying plasma behavior and phenomena occurring are similar to those expected in a power plant—and thus with relevant β, current profile, rotation, electron heating, collisionality, etc., so that models can be validated that capture the relevant physics for reactor projection. Dissipative divertor, and likely full detachment, combined with radiative impurity mantles within the separatrix, will be necessary to present plasma facing components with a tolerable challenge and eliminate erosion so the device can run continuously for months or years. These considerations also require development of ELM elimination techniques to prevent divertor erosion. Finally a fall back safe plasma quenching technique must be resolved in order to prevent disruptions should control or system failure occur.
Considering physics emphases for particular scenarios, the high qmin path requires operation substantially above the no wall ideal MHD stability limit, and thus either additional inherent kinetic stabilizing mechanisms or magnetic feedback control. The high li path is more reliant on the development of new and more efficient current drive tools—though these are highly levering for all concepts to reduce recirculating power. The hybrid scenario provides a degree of self-optimization for the current profile (through flux pumping) which must be understood. High li and hybrid are also more susceptible to tearing modes. Beyond the plasma itself, there also remain many hardware, engineering, diagnostic and control challenges, though we leave these topics to other publications—though do note that there is a strong need for an extensive technology and engineering program to develop solutions. We focus here on the advanced tokamak physics.
Simulation Tools
Theory-based integrated scenario modeling plays an essential role in the development of self-consistent high βN steady-state scenarios on DIII-D in a repeated cycle of scenario design, experimental implementation, and model validation. At the heart of this is the FASTRAN suite [49, 50], which is an efficient and robust iterative solution procedure to find a steady-state solution (d/dt ~ 0) of core transport, self-consistent with external heating/current drive, MHD equilibrium, ideal MHD stability, and edge pedestal, built upon a modern integrated modeling framework, Integrated Plasma Simulator (IPS). Recently, remarkable progress has been made in improving the individual elements of the FASTRAN modeling, such as a comprehensive theory-based core transport model, TGLF for all transport channels (particle, energy, and momentum), and EPED for edge pedestal to provide the boundary condition of the core transport. Integration of such high-fidelity core transport and edge pedestal models along with the well-established modeling of MHD equilibrium (EFIT), ideal kink stability (DCON, GATO) and external heating/current drive (NUBEAM, TORAY, GENRAY) has substantially advanced our predictive capability for the steady-state operating scenario development without relying on any significant free input parameters.
The FASTRAN modeling reproduces most features of DIII-D high βN discharges in the stationary condition. Figure 6 shows a comparison of the FASTRAN-predicted stationary profiles at t = ∞ with the measurements during the high βN phase of an elevated qmin > 1.5 discharge at βN ~ 3, which was sustained by the off-axis NBI and ECCD longer than 2τR. The calculated radial profiles of ne, Te, Ti, and Ω reproduce the measurement reasonably well. The predicted plasma current profile (Fig. 6e), to which the discharge would eventually evolve, is close to the estimation by kinetic EFIT equilibrium reconstruction obtained with MSE and the calculated edge bootstrap current as constraint. The proximity of these two profiles both (1) improves confidence that FASTRAN contains most of the important physics, and (2) confirms that the experimental discharge was approaching a stationary state.

Taken from [50]
Calculated radial profiles (red) compared with experimental measurements (blue): a electron density, b electron temperature, c toroidal plasma rotation, d ion temperature, e surface-averaged parallel plasma current density, and g safety factor. The shade denotes a random error bar for the time-varying experimental profile averaged over 4 < t < 5 s during stationary high βN phase. The calculated profiles are plotted at the end of the 4th (dashed) and 5th (solid) iterations of the steady-state solution procedures to update the sources, MHD equilibrium, and boundary conditions. The vertical line shows the location of the edge pedestal top.
In addition to guiding the DIII-D experiment and H/CD upgrade ("Future Research Requirements and DIII-D’s Role" section), the same FASTRAN modeling has been used to extrapolate the steady-state scenarios developed on DIII-D to future reactors such as ITER [51] and C-AT DEMO [52; journal paper in preparation], thereby identifying gaps between the present-day experiments and future reactors, and further research needs on DIII-D. One such example for the ITER projection is shown in Fig. 7, predicting that fully non-inductive hybrids described in section "Steady State Hybrid with RMP-ELM Suppression" can achieve the Qfus = 5 ITER steady-state mission.

Adapted from [51]
Self-consistent profiles for ITER steady-state Qfus ≈ 5 case from FASTRAN simulation if pedestal is increased over EPED predictions: a electron and ion temperatures, b electron, fuel ion and helium ash densities, c toroidal rotation and d ECCD, NBCD, bootstrap and total current densities (the bootstrap peak in the core is a numerical issue).
It should be noted that in this work, while the transport models can make projections, and do in same cases get good agreement with experiment (Fig. 6), these models remain to be fully validated, particularly with more advanced current profiles and higher \(\beta_{N}\) required for steady state scenarios. This is an area of progress set out in the paper, but also a major research goal of ongoing work set out in section "Future Research Requirements and DIII-D’s Role", with significant discrepancies emerging at high \(\beta_{N}\) and broader profiles, and further work to do to more fully understand electron transport and multi-scale effects.
Progress in the Development of Candidate Steady State Operating Scenarios
In recent years DIII-D has made significant progress in the development of the candidate operating scenarios. With near term plans on the facility including a significant increase in off-axis current drive in 2019 (see section "Future Research Requirements and DIII-D’s Role"), work on plasma scenario development has focused key tests of principle, including the physics and integration of key techniques such as ELM mitigation or radiative divertor, development of underlying physics understanding, and demonstration of particular performance access and techniques. Fuller exploration of scenarios that are more accessible with the present facility configuration, such as the steady state hybrid and the high βP regimes have provided a basis for such technique development and more integrated physics tests. Considerable effort has also been devoted to the development of advanced control strategies, such as model based profile control, which is providing real benefits in the development of more stable access paths to higher performance regimes.
Steady State Hybrid with RMP-ELM Suppression
Experiments on DIII-D have demonstrated the potential of the hybrid scenario as a regime for high-beta, steady-state plasmas with 1 MA of plasma current driven non-inductively and βN up to 3.7 sustained for ~ 3 s (~ 1.5 current diffusion time, τR) [44, 45]. The hybrid scenario is a long duration, high performance, H-mode regime that operates near qmin≈ 1 with higher confinement and greater stability compared to the conventional H-mode regime. The hybrid scenario in the presence of a small 3/2 NTM has the attractive property of a self-organized current profile that derives from a “flux pumping” mechanism transferring part of the central current drive to an off-axis position [46, 53]. This allows all of the current drive to be located near the plasma center where the efficiency is high without forcing qmin below 1 and triggering significant sawtooth activity.
In steady-state hybrid experiments on DIII-D, the surface loop voltage is driven down to zero for > 1 τR when the poloidal β is increased above 1.9 at a plasma current of 1.0 MA, co-NBI power of 11 MW and ECCD power of 3.2 MW. Figure 8 shows that theoretically the central current is strongly overdriven in these steady-state hybrids owing primarily to the efficient on-axis ECCD. Despite this, the measured plasma current profile remains broad and shows no sign of peaking during the ~ 3 s high-beta phase (TRANSP simulations predict that qmin should drop well below 1). The confinement quality is excellent (H98y2 ~ 1.6) and increases approximately with the square root of density. Stationary operation is sustained at pressures above the calculated ideal no-wall limit and 80–90% of the ideal with-wall MHD limit (the latter calculated to be βN ~ 4–4.5). High-beta hybrids heated only by NBI typically have TAE/EAE energetic particle modes that increase the beam ion transport. By applying ECCD to achieve complete current drive, these EP modes are replaced by a more benign fishbone-like instability, possibly because ECCD depresses qmin closer to 1, which lessens the beam ion transport.
Calculated plasma current density profile (red) and measured current density (black) for an on-axis (full lines) and an off-axis NBI discharge (dash lines). The radial localization of the 3/2 NTM is represented by the green shaped area.
The steady-state hybrid scenario with ITER relevant values of beta, collisionality, safety factor and plasma shape has been successfully integrated with ELM suppression by applying an odd parity n = 3 resonant magnetic perturbation (RMP) [51]. Figure 9 shows an ELM suppressed hybrid with IP = 0.95 MA, βN = 3.0, βP = 1.9 and H98y2 = 1.2 using 3.5 MW of on-axis ECCD and 9.9 MW of co-NBI. The measured surface loop voltage is zero and the modeled non-inductive currents equal the plasma current. Experiments also demonstrated that 0.95 MA hybrids with RMP ELM suppression could be maintained with a flat (and zero) loop voltage profile when the central solenoid current was frozen between 2.5 and 5.5 s. The RMP stabilization of type-I ELMs is predominantly through density pumpout, partially compensated by increased pedestal temperature, which shifts the pedestal from the unstable region for peeling–ballooning modes to the stable region. A new finding in this steady-state hybrid regime from ideal MHD modeling using the GPEC code is the presence of one dominant marginally stable mode in the plasma edge that couples effectively to the n = 3 RMP, producing an edge magnetic perturbation 2–3x the amplitude of the applied vacuum field [54].
Time history of steady-state hybrid discharge with ELM suppression: a total plasma current and non-inductive components from ECCD, NBCD and bootstrap current, b surface loop voltage, c normalized beta, safety factor minimum and RMP coil current, d divertor Dα light.
Two different extrapolation methods, ρ* scaling and theory-based modeling from FASTRAN simulations, show that these steady-state hybrids can satisfy the ITER steady-state mission with a fusion gain of Q ≈ 5 and a required current drive power of ≈ 100 MW for 100% non-inductive operation.
High li Scenario
Increased confinement and ideal stability limits at relatively high values of the internal inductance (li > 1) enable an attractive scenario for steady state tokamak operation at high βN. Many of the features of such a discharge have been demonstrated in DIII-D, and the highlights of the most recent experiments [48] are reviewed in this section. The improvements in confinement and stability arise largely as a result of higher poloidal field in the discharge core and larger magnetic shear in the outer half of the plasma when the current density profile is more peaked. Plasmas with high li and βN ≈ 4–5 are predicted by theory to be stable to low toroidal mode number (n) ideal MHD instabilities even without the effect of a conducting vacuum vessel wall [55, 56]. In addition, the βN limit as determined by the infinite-n ballooning mode is expected to increase with li [57]. These features make a high li discharge a candidate for a power plant that could either operate stably at βN ≈ 4 without the requirement for a nearby conducting wall or n ≥ 1 active stabilization coils, or at βN ≈ 5 with wall stabilization. A more detailed description of the history of the experimental and theoretical study of discharges at high li can be found in Ref. [48]. Here, \(l_{i} = \int {dV} B_{P}^{2} /V/\left( {\oint {B_{P} dl} /\oint {dl} } \right)^{2}\) where BP (T) is the poloidal magnetic field, V (m3) is the plasma volume and the path for the line integrals is the plasma boundary.
Steady-state tokamak operation is optimum with a high fraction of bootstrap driven current (fBS), but typical bootstrap current density (JBS) profiles can have limited compatibility with an elevated value of li. The dependence of the stability limit to βN on li strengthens as the core pressure profile is broadened [55] and stability limits are highest with high plasma elongation κ and triangularity [34, 56]. A broad core pressure profile and strong discharge shaping both increase JBS in the outer half of the plasma. In addition, there is a localized peak in the bootstrap-driven current in the H-mode pedestal region at the edge of the plasma as a result of the steep pressure gradient there. As the fraction of Ip resulting from bootstrap current in the outer half of the plasma increases, the maximum value of li that can be obtained by tailoring the profile of the externally-driven current density will decrease. Taking this into account, the expectation is that there is an optimum value of li [56] where there is a compromise between high li and high fBS: li ≈ 1, βN = 3.5–4.0, and fBS ≈ 0.5. For fully noninductive operation, about half of the current would be provided by externally-driven current near the axis. Although the total amount of externally-driven current would be relatively large, the required external current drive power could be comparable to what is required for other steady-state scenarios because of increased efficiency for external current drive near the axis.
The significant advantages of high li operation are reflected in the most recent DIII-D experimental results [48]. In a double-null divertor configuration, discharges have been produced with βN ≈ 5 and excellent confinement H98(y,2) ≈ 1.8, parameters that are in the range required for a high power density reactor. Discharges were obtained with βN > 4 sustained for 1 s (≈ 0.5τR), and with brief, tearing mode-limited phases with βN > 5 (Fig. 10). High li is presently the only method to access βN this high in conventional aspect ratio tokamaks, although similar βN values are projected for a scenario with a broad current density profile and qmin > 2 ("Simulation Tools" section).

[Taken from 48]
Time evolution of parameters in two high li discharges with high βN. A discharge with βN sustained above 4: aβN and divertor-region Dα, bli and H98(y,2), c the amplitude of n = 1 and n = 2 poloidal field fluctuations. ne ≈ 5.5 × 1019 m−3 at t = 3.1 s dropping to ne ≈ 4.5 × 1019 m−3 by t = 4.3 s. A discharge that has βN exceeding 5 for a short interval: dβN and divertor-region Dα, eli and H98(y,2), f the amplitude of n = 1 poloidal field fluctuations. ne ≈ 6.7 × 1019 m−3the peak βN. BT = 1.7 T, Ip = 0.8 MA in both cases.
The high li, high βN discharges have not yet been operated with a stationary current density profile as sufficient externally-driven current is not yet available (but planned upgrades are projected to address this—see section "Future Research Requirements and DIII-D’s Role"). Thus the decrease in βN with time in Fig. 10a occurs because of the decrease in confinement as li decreases with constant beam power. In this case, the total calculated noninductively driven current exceeds the total plasma current as a result of the high βN and the relatively large q95 ≈ 7.5, with bootstrap current fraction fBS ≈ 0.8, and a negative surface voltage applied by the control system to maintain the target value of Ip. However the li is not sustained because the current is not distributed centrally enough to maintain it. Further current drive upgrades and work to control pedestal height are projected to address this.
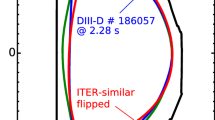
Discharges in the planned ITER shape, scaled to fit into the DIII-D vacuum vessel, have been studied with q95 ≈ 4.8, li ≈ 1, and βN ≈ 3.5, near the parameter range anticipated for steady-state operation in ITER (Fig. 11). In this case, fNI < 1 as a result of the lower βN and q95. Discharge performance was close to the estimated requirement for the ITER steady-state mission with G = βN H89/q295 ≈ 0.3 (Fig. 11d).

[Taken from 48]
Parameters in a discharge operated in the ITER scaled shape. aβN and divertor-region Dα, b internal inductance and normalized confinement, c amplitude of n = 1 and n = 2 poloidal field fluctuations, d the fusion gain factor, e the measured surface voltage, and f the noninductive and bootstrap current fractions. BT = 1.7 T, Ip = 0.92 MA.
A high li scenario is a possibility for ITER in the event that the H-mode pedestal pressure is found to be too low to achieve the target fusion gain for the steady-state mission at high qmin > 2. ELM mitigation using 3D magnetic fields, for instance, can reduce the pedestal density and pressure, an effect that would reduce the bootstrap current density near the plasma boundary, leading naturally to increased li. The effect of a reduction in the H-mode pedestal pressure was tested in DIII-D by applying n = 3 fields from the internal non-axisymmetric coils. As the n = 3 field amplitude was increased, the pedestal pressure decreased along with the calculated fraction of Ip supplied by bootstrap current in the pedestal region. A corresponding increase in the average value of li during the high βN phase was observed.
The high values of βN attained at high li are close to, but below, the calculated limits set by the ideal n = 1 kink and the ideal infinite-n ballooning instabilities (Fig. 12 [48, 58]). Consistent with the stability calculations, a global, pressure-limiting instability has not yet been clearly observed in the experiment. Instead, in the cases where stability determines the limit to performance, the observed mode is most commonly an m = 2/n = 1 resistive tearing mode (e.g. Fig. 10d–f). In the ITER scaled shape (Fig. 11), the value of βN that could be sustained for the full discharge duration was limited by the 2/1 resistive mode to a value below the no-wall ideal limit (Fig. 12b).

[Taken from 48]
Ideal MHD n = 1 stability limits calculated without including the effect of the conducting vacuum vessel wall (triangles) and including the wall (diamonds). a Double-null divertor shape discharge shown in Fig. 10a–c. Here the squares are the ideal infinite-n ballooning mode stability limit calculated using the BALOO code [58]. b ITER shape discharge shown in Fig. 11. The lines are sketches to indicate the location of the various sets of data points.
A power plant relevant method to form the high li equilibrium has been demonstrated. The discharge is begun with an initial, low βN phase with only inductive heating so that the electron temperature is low and the characteristic timescale for relaxation of the current density profile is very short. The discharge remains in these conditions long enough for the current profile to evolve to a stationary, peaked-on-axis state prior to the application of the external heating and current drive power. There is no requirement for rapid changes in Ip, elongation or radius as used in the past to increase li, techniques which would be difficult to implement in a large device with superconducting coils.
Transport code modeling studies have been used to explore how increased current drive and heating powers in DIII-D (13 MW off-axis neutral beam, 9 MW ECCD) could be applied to maintain a stationary, fNI = 1 high li discharge. The FASTRAN framework [49] was used to calculate a stationary current density profile solution using theory-based bootstrap current, current drive and transport models. With the goal of maximizing the stationary value of βN consistent with the calculated stability limits, the current drive and heating powers, the deposition profiles for the ECCD sources, and the relative fractions of on-axis and off-axis neutral beam powers were varied. The result from this initial modeling study (Fig. 13) is close to the “optimum” solution found in [56] with li = 1.07, βN = 4, fBS = 0.5, fNBCD = 0.35, fECCD = 0.3, H89 = 2.3, H98(y,2) = 1.1, and the ideal n = 1 stability limits βN ≈ 4.1 without a conducting wall and βN = 4.8 with a wall. All of the available off-axis neutral beam power is used in order to broaden the fast ion pressure profile, thus minimizing the peaking of the pressure profile which reduces the stability limit. The off-axis neutral-beam-driven current density is minimized, though, through choice of the toroidal field direction [59].

[Taken from 48]
Current density profiles in the βN = 4 transport code-modeled steady-state solution for DIII-D. BT = − 2 T, Ip = 1.1 MA, q95 = 6, total injected neutral beam power is 20 MW with 13 MW injected off axis, and the ECCD power is 9 MW.
Continued development of a high li steady-state scenario requires work in several areas. The onset of the resistive tearing mode, particularly at βN near the ideal mode limits, must be understood as these modes presently set the observed stability limit. Improved capability to avoid the 2/1 mode would enable the study of discharges with the combination of βN and q95 that results in fNI = 1. The understanding of the parameters in the H-mode pedestal region should be refined as the pressure and current density there play significant roles in determining the self-consistent values of li and βN. Finally, development of the capability to provide the required externally driven current near the axis is needed in order to be able to operate high li discharges in a stationary, rather than the present transient, manner. In DIII-D, the expectation is that stationary operation would be enabled by an increase in the available ECCD power to approximately 9 MW (see section "Future Research Requirements and DIII-D’s Role"). A method to mitigate the limitations on the current density at the axis imposed by the sawtooth instability [60] would allow more of the current to be driven closer to the axis, increasing efficiency and also providing access to higher values of li.
High qmin Scenario
The high qmin scenario focuses on q95 ≤ 6 with q(0)–qmin< 0.5. This approach has been studied at DIII-D because, with broad pressure profiles, it scales to high βT, and thus high Q, in a power plant. Close to fully non-inductive plasmas with durations approaching the current redistribution timescale, τR, have been achieved in DIII-D with 1.5 < qmin < 2 and current density peak value at ρ ≈ 0.3 [39], q95≈ 6.2, and βN≈ 3.7. These discharges were achieved with all on-axis NBCD and a broad ECCD distributed about the mid-radius. Ideal stability analysis showed that these discharges operate only marginally below the n = 1 kink mode ideal-wall βN limit (3.7–4), as a result of insufficiently broad current and pressure profiles. Such operational proximity to an ideal MHD limit is understood to risk tearing mode instability—i.e., a 2/1 tearing mode in this case.
The introduction of off-axis neutral beam injection led to improved capability to operate with broader current and pressure profiles to increase βN limits [40, 41]. Discharges with 1.4 < qmin < 2 and 5 < q95 < 6.2 were explored with βN ≈ 3.5 for durations lasting up to 2τR (3 s). The most interesting cases from an ideal stability point of view had q95≈ 5 and qmin≈ 1.4—an example is shown in Fig. 14. While only 70–75% non-inductive at this q95, these plasmas were nonetheless quasi-stationary, and had predicted n = 1 ideal-wall βN limits near 4.5. In most discharges with 1.4 < qmin < 2 using off-axis NBI, off-axis fishbones were observed that are likely responsible for some inferred anomalous fast ion transport. Most plasmas with qmin just below 2 (~ 1.8) had the high βN phase terminated by 2/1 tearing modes.

Reprinted from [41]
Example of elevated qmin DIII-D discharge using off-axis NBI.
Off-axis NBI also clearly improved the ability to sustain plasmas with qmin > 2, but thus far at reduced maximum βN (~ 3.2) and fNI, largely as a result of increased fast ion transport caused by unstable Alfven eigenmodes (AE) [61]. AE stability was found to be sensitive to gradients of fast ion β. When a critical gradient is exceeded, multiple overlapping AE resonances cause fast ion redistribution or loss if further beam heating is applied [62] (see section "Energetic Particle Physics"). This lowers the NBI heating and current drive effectiveness and global energy confinement. When the lost heating power is accounted for, power balance analysis showed qmin > 2 plasmas have thermal transport similar to plasmas with lower qmin.
Experiments and modeling have shown a variety of options for improving fast ion confinement in DIII-D qmin > 2 discharges. Modeling predicts, and some experimental evidence confirms, that further broadening of the q-profile can reduce AE-induced fast ion loss [63]. Specifically, increasing q0 is predicted to eliminate Toroidal AEs by closing off the frequency gap in which they can exist, and increasing the radius of qmin is predicted to lower the impact of Reverse Shear AEs on fast ion confinement by pushing the modes to a region of lower fast ion density. Planned increases in off-axis ECCD and NBCD in the next few years will enable further tests of this. Prompt AE stabilization using ECH applied at ρqmin has also been demonstrated [64]. In this case ECH is thought to modify RSAE existence and damping through changes to the local pressure and pressure gradient. Variable NBI voltage and current at fixed power has also been developed. At reduced beam voltage, reduced AE-drive in high-qmin discharges has been shown to result in improved performance. [65, 66]. The physics of these processes is discussed further in section "Energetic Particle Physics".
Other DIII-D experiments have explored properties of qmin> 2 plasmas with broader current profile using a transient technique. Dynamically ramping down the toroidal field induces current density broadly distributed in the outer half radius, effectively mimicking non-inductive current drive sources that will be available after future upgrades [67]. Using this technique, plasmas with qmin> 2 were produced that had excellent normalized global energy confinement (H89 = 2.5) [68]. Using fast RWM magnetic feedback enabled access to βN = 4. This corresponds to the predicted ideal-wall n = 1 kink mode limit, and indeed quickly growing instabilities consistent with an internal kink were observed. The reasons for the improved energy confinement compared to other qmin> 2 discharges described above still needs to be determined. Possible contributors include: improved thermal confinement from internal transport barriers, increased density and shorter fast ion slowing down time, and broader q-profile.
High βP Scenario
Experimental and modeling investigations performed in the last few years by an international joint team of scientists working on DIII-D and EAST have made great progress toward developing the high poloidal beta (\(\varepsilon \beta_{P}\) ≥ 1) regime as a basis for the steady state operation of a tokamak fusion reactor [37, 69,70,71,72,73,74,75]. Plasma operation in the high poloidal beta regime ameliorates two key weakness of the tokamak configuration: current disruptions and the need for external current drive. Operating a tokamak at high \(\beta_{P}\) offers low disruptivity because of high safety factor [\(q_{95} \propto \varepsilon \beta_{P} /\beta_{N}\), where \(\beta_{N} = \beta_{T} /\left( {I_{P} /aB_{T} } \right)\), with the toroidal plasma current], and low external current drive requirements because of high self-generated bootstrap current fraction (\(f_{BS} \propto \sqrt \varepsilon \beta_{P}\) assuming constant collisionality). Conversely, since the plasma current is relatively low at high \(\beta_{P}\), maintaining a high fusion power density generally requires operation at high \(\beta_{N}\), and at confinement quality higher than standard H-mode. As discussed in section "Criteria for Steady State Fusion and Key Metrics", operation at high \(\beta_{N}\) does not increase disruptivity—see Fig. 1, taken from the DIII-D disruption database.
Experiments and simulations have shown that energy confinement quality higher than standard H-mode (enhancement factor over H-mode confinement scaling H98y2 > 1) can be achieved and sustained in the high \(\beta_{P}\) regime independently of the plasma rotation, thanks to a key feature of the high \(\beta_{P}\) regime: the high Shafranov shift of the plasma equilibrium, which can provide turbulence suppression via local magnetic shear [76], and can lead to the formation of an internal transport barrier (ITB) in the kinetic profiles at large minor radius [see refs above]. Furthermore, the investigations have addressed several of the outstanding issues previously highlighted in the literature regarding operation with ITBs, by demonstrating ITB formation and sustainment at high Greenwald density fraction, lack of impurity accumulation, sustainment of the large radius, compatibility with a high \(\beta_{N}\) limit, and robustness of the self-organized configuration.
These experimental results have been used to validate MHD, current drive, and turbulent transport models, and to project the high-βP regime to a reactor. In a burning plasma, it is found that the Shafranov shift alone may not suffice to provide improved confinement (over standard H-mode) without rotation and rotation shear. However, making the core magnetic shear more negative provides a similar turbulence suppression mechanism to Shafranov shift, and can help devices such as ITER and CFETR achieve their steady-state fusion goals.
An example of high \(\beta_{P}\) discharge obtained on DIII-D and illustrating several of these features is shown in Fig. 15. The plasma cross section is a double-null divertor shape with elongation κ ~ 1.9 and average triangularity < δ> ~ 0.6. After an appropriate equilibrium is established (~ 1.7 s) the current in the Ohmic heating coil is clamped, so that the plasma current is forced to relax noninductively. This discharge achieves and maintains \(\beta_{P} \sim\beta_{N}\) ~ 3.3 with \(f_{BS}\) ≥ 70%, an excellent energy confinement quality (H98y2 ~ 1.5) associated with the formation of an ITB at large minor radius (ρ ~ 0.7) in all channels (density, temperature, rotation, see e.g. [37]), Greenwald density fraction \(f_{Gw}\) ~ 1, and constant radiated power throughout the high \(\beta\) phase. The significant oscillations in the \(\beta\) traces are due to bursty ELM-like events driven by pedestal gradients and dominated by n = 1 [37], rather than higher n as most ELMs. Despite the severity of these perturbations, the ITB and a broad current profile with elevated minimum safety factor qmin≥ 3 are maintained in fully noninductive conditions for about 3 current relaxation times (\(\tau_{R}\) ~ 1 s).
Time traces of representative high \(\beta_{p}\) discharge 154,405: a Total plasma current, bootstrap component, and surface toroidal voltage; b\(\beta_{P}\), \(\beta_{\text{N}}\), H98y2 and the Greenwald fraction; c Total radiated power, neutral beam injection power, and electron cyclotron power; d minimum safety factor. Vertical dashed line marks time when the Ohmic heating coil current is fixed. From: A.M. Garofalo et al., Plasma Phys. Control. Fusion 60 (2018) 014043
While the discharge of Fig. 15 has very high q95~ 10, DIII-D experiments have also showed that excellent energy confinement quality can be maintained when q95 is reduced towards reactor relevant values of q95≤ 7, as long as \(\beta_{p}\) is maintained above a threshold value ~ 1.9 for ITB formation (see Fig. 16). With reduced Shafranov shift at lower q95 and βp, negative magnetic can be utilized to contribute to suppression of turbulence. Reverse shear has been predicted to lower the βp threshold for the ITB in ITER and CFETR. So far, the extension to lower q95 has been carried out inductively. Future experiments on DIII-D will aim to extend the fully-noninductive high \(\beta_{P}\) regime with ITB to q95~ 6 by operating closer to the \(\beta_{N}\) limit ~ 4.5.
Comparison of two DIII-D discharges with \(\beta_{P}\) ramp-down. Presence of strong ITB is indicated by H98y2 > 1.5. Discharge without off-axis NBI (red) loses the ITB permanently when \(\beta_{P}\) ≤ 1.9, while discharge with off-axis NBI (blue) develops negative magnetic shear at large minor radius and intermittent ITB at the same \(\beta_{P}\). From: A.M. Garofalo et al., Plasma Phys. Control. Fusion 60 (2018) 014043
Radiative Divertor Progress in Advanced Tokamak Plasmas
Future highly-powered, high performance tokamaks will be confronted with the requirements to simultaneously avoid potentially damaging power loads at their divertor targets, maintain desirable plasma performance (e.g. energy confinement), and sustain adequate pumping for particle control. Two general approaches that have been considered by the DIII-D program for dealing with this problem include dissipating heat flux at the divertor targets by (1) increasing the radiated power inside the main plasma and/or in the divertor and by (2) increasing the poloidal flux expansion at the divertor targets. While these approaches or variation of these approaches have been successfully applied to more conventional single-null divertor (SND) cases [77,78,79,80,81,82], we have found their successful applications to highly powered, high performance double-null divertor (DND) cases on DIII-D to be more challenging. Because DND shapes have been shown to provide superior stability and confinement properties [83, 84], our focus here has been on applying these divertor heat flux reduction solutions to highly shaped, double null and near-double null divertor (DND) configurations. In this section, we review recent studies where radiating divertor and flux expansion techniques were applied to DIII-D high performance (AT) plasmas.
-
1.
Radiating divertor Several investigations have shown that significant reductions in heat loading are possible by enhancing the radiated power upstream of the divertor targets through a combination of deuterium and impurity injection, e.g. “puff-and-pump” [79]. This approach has two principal ingredients. First, “seeding” the divertor with impurity particles can radiate away a significant fraction of the power flow into the divertor before it can impact the divertor structures. Second, a strong flow of deuterium ions streaming along the upstream scrape-off layer (SOL) into the divertor can inhibit the escape of these impurities from the divertor by a combination of upstream deuterium gas puffing and active particle exhaust at the divertor targets. Along these lines, DIII-D has demonstrated improved energy confinement by injecting neutral deuterium gas into high performance near-double null divertor (DND) plasmas during low- and moderate power input [84, 85]. For example, at moderate power input (PIN) and normalized plasma beta (βN), i.e., 9–12 MW and 2.5–3.0, DND plasma performance was optimally maintained when argon seeds were used, in comparison with the nitrogen or neon seed alternatives. With argon there was considerably less fuel dilution in the main plasma and lower Zeff for the same factor of two reduction in peak divertor heat flux (qP). During the pre-puff phase of these discharges, qP typically ranged from 2.5 to 4.0 MW/m2 [86]. Deterioration in the energy confinement time was typically less than 10–15%.
A significant effort has been made to extend puff-and-pump scenarios to even higher levels of power input in DIII-D. While plasma conditions at lower-to-moderate power input were found to be favorable to successful puff-and-pump radiating divertor applications to the DND, plasma response to higher power input resulted in a more complicated picture. Recent studies [85] have shown that improved energy confinement is possible during gas puffing under certain conditions for near-double null divertor (DND) plasmas, e.g. q95 ≥ 6, PIN ≥ 13–15 MW, H98 = 1.4–1.8, and βN = 3.5–4.0. In marked contrast to lower powered high performance plasmas, both τE and βN in high power cases increased and ELM frequency decreased, as density was raised by deuterium gas injection (Fig. 17). This improved performance in the higher power plasmas was tied to higher pedestal pressure, which according to peeling–ballooning mode stability analysis using the ELITE code [87] could increase with density along the kink/peeling stability threshold, while the pedestal pressure gradient in the lower power discharges were limited by the ballooning threshold [85]. This resulted in improved fueling efficiency and ≈ 10% higher τE and βN than is normally observed in comparable high performance plasmas on DIII-D. Applying the puff-and-pump radiating divertor approach at high versus moderate power input was shown to result in a much different evolution in core and pedestal plasma behavior. We have found that injecting deuterium gas into these highly powered DND plasmas can open up a new avenue for achieving elevated plasma performance, including better fueling, but this improved fueling may also have a downside when applied to a radiating divertor approach to divertor heat flux reduction. Just as fueling the main plasma by gas puffing can be less formidable for a DEMO-class plasma, the same also applies to impurity seed “fueling” of the core and, if uncontrolled, an unacceptable drawback is the possibility of deleterious accumulation of these impurities in the core.

[From Ref. 85]
a The energy confinement time τE is plotted against line-averaged density at two distinct power levels, i.e., 10.5 MW (red circles) and 14.4 (black squares). b The ELM frequency νELM is plotted against line-averaged density for the same data set. Density was raised by injecting deuterium gas.
(2) Divertor poloidal flux expansion A second approach in reducing divertor heat flux that has been studied on DIII-D relies on shaping the divertor flux surfaces in advantageous ways. Increasing the poloidal flux expansion at the divertor targets spreads power loading over a wider target (“wetted”) area. One very promising and sophisticated approach that was tested in a high performance regime has been referred to the “Snowflake” divertor configuration [88]. The Snowflake divertor has been shown to be effective in dissipating heat flux at the divertor target for more conventional single-null H-mode discharges in both NSTX [89] and DIII-D [90] at modest power input. We examined a Snowflake-double-null divertor hybrid (SF-DN), which was configured by: (a) adding a second X-point near the outer target of the primary divertor, and (b) preserving the conventional double-null shape in the secondary divertor (Fig. 18b; [91]). The poloidal flux expansion at the outer divertor target of the primary divertor was significantly increased and the incoming power flow to this outer divertor was much more dispersed compared with a more conventional divertor configuration that does not have this second X-point. Compare the conventional DND (Fig. 18a) with the Snowflake-DN hybrid (SF-DN), as shown in Fig. 18b. Both configurations were biased slightly toward the lower divertor. High performance SF-DN plasmas largely mirrored the high performance characteristics of DNDs under both radiating- and non-radiating divertor conditions. This was not unexpected, because these SF-DN and DND plasmas had very similar poloidal cross-sections, upper and lower triangularities, and q95 (≅ 5.0–5.2). Because of their nearly identical lower inner divertor geometry and poloidal flux expansion (≅ 6.6), both SF-DN and DND heat flux profiles at their respective inner divertor targets were similar, both prior to and during the radiating phases (Fig. 18a1, b1). On the other hand, the advantage of the SF-DN was tied to a much larger poloidal flux expansion at its lower outer divertor target, i.e., ≅ 28 for the SF-DN versus ≅ 9 for the DND; the result was a factor of two lower peak heat flux at the outer divertor target with the SF-DN shape, both before and during deuterium gas injection operation (Fig. 18a2, b2). One notes that q⊥,P at the lower outer divertor target for the SF-DN in the non-radiating divertor case was still lower than q⊥,P for the corresponding DND in the radiating divertor case. Control of snowflake configurations has been raised as a concern for future reactors, as small vertical perturbations could lead to large strike point motions; on DIII-D, we have found control to be sufficient to maintain appropriate geometry, though this affect does lead to some modest beneficial heat flux spreading.

(Adapted from data presented in Ref. 91)
a DND that is magnetically biased toward the lower (primary) divertor (dRsep = −0.5 cm), b double-null with “Snowflake” lower divertor and upper (secondary) divertor (SF-DN) similar to the DND to a. Heat flux profiles of the lower inner (a1) and outer (a2) divertor targets of the DND and corresponding SF-DN during both non-deuterium puff (red) and full radiating divertor (blue) cases; Inner and outer divertor target of the DND (a1, a2); and SF-DN (b1, b2). Parameters: q95 = 5.2, H98(y,2) = 1.2–1.4, PIN = 10 MW, and ne/nG = 0.45–0.60.
Controlling the particle inventory in the SF-DN from the primary divertor was difficult because particle flux in that divertor was spread out, making particle pumping difficult. For single-null Snowflake divertors, this would present a serious obstacle. DIII-D studies have shown for the hybrid SF-DN, however, that adequate pumping from the secondary divertor which has DND shape can provide significant pumping to help compensate for weak pumping in the primary divertor.
More reactor relevant DND plasmas that produce significant power outflow will very likely have peak divertor heat flux levels well above 10 MW/m2 and thus require reliable methods of reducing excessive heating to the divertor structures. While several studies at DIII-D have found modest reductions in divertor heat flux under AT DND conditions are possible without acute deterioration in high performance, these experiences suggest, however, that no single approach will be adequate by itself to satisfy the severe requirements for divertor heat flux reduction DEMO-class plasma conditions. Future work will doubtless focus on advantageously combining different approaches to achieve the three goals of significant divertor heat flux reduction, maintenance of plasma performance, and adequate pumping—cognizant at the same time that plasma transport behavior can change as power input changes.
Advances in Underlying Physics
Achievement of an understanding of the advanced scenarios discussed in the previous section and the projection of scenarios to future reactors present new physics challenges. The DIII-D program has explored plasma behavior utilizing a large range of perturbative techniques, variation of parameters and extensive diagnostic capabilities in order to help develop the required understanding and validated physics models.
Validation of Current Drive Models
DIII-D experiments on Neutral Beam Current Drive (NBCD) have clearly demonstrated off-axis NBCD as expected from modeling [92,93,94]. Off-axis current drive is critical in testing the potential of high bootstrap fraction, steady-state operation with a broad current profile at elevated q, especially for qmin > 2 (section "High qmin Scenario"). For validation of off-axis NBCD physics, the local NBCD profile driven by the new tilted beams was measured in H-mode plasma and compared with modeling under a range of beam injection and discharge conditions such as the toroidal magnetic field direction, beam injection power, plasma beta and ratio of beam injection energy to electron temperature (Eb/Te).
The full radial profile of NBCD measured by the magnetic pitch angles from the motional Stark effect (MSE) diagnostic (Fig. 19) shows a clear hollow in NBCD with the peak NBCD location at ρ ~ 0.45. This is in good agreement with the classical model calculation using the beam-ion orbit following Monte-Carlo beam ion slowing down code, NUBEAM. (Note that the orbit following nature of NUBEAM means that the calculated NBCD includes the fast-ion bootstrap current. Other analytical expressions have been derived to explicitly calculate the bootstrap current from alpha particles [95] and beam ions [96], with [96] finding the beam-ion bootstrap current is less than one-tenth the bulk bootstrap current at the same pressure gradient.) Time evolution of the MSE signals is consistent with transport simulation with realistic current drive sources. The beam-stored energy estimated using equilibrium reconstruction, neutron, and fast-ion D-alpha data do not show any noticeable anomalous losses of NBCD and fast ions. The measured magnitude of off-axis NBCD (Fig. 20) is very sensitive to the toroidal magnetic field (BT) direction that modifies the alignment of the off-axis beam injection to the local helical pitch of the magnetic field lines. The NBCD profile for the BT direction in poor alignment shows substantially reduced NBCD (~ 45%) as well as inward shift of the peak NBCD location (Δρ ~ 0.1). This dependency of the off-axis NBCD efficiency on the BT direction is crucial to optimum use of the off-axis beams not only in DIII-D but also for application in ITER.
Measured NBCD profiles for on (blue) and off (red) axis injection. NUBEAM modeling is shown with solid lines [from 94]
Dependency of measure off-axis NBCD on toroidal field direction [from 94]
Turbulent Transport in High β Scenarios
Transport is expected to be modified in high β scenarios through two principle effects. Firstly the turbulence can be reduced when local magnetic shear is increased on the outboard ballooning side. This naturally occurs in high li and high qmin scenarios. In the high li, a high average magnetic shear arises, driving up local shear. In the high qmin this is also found to occur as the weakening of the average magnetic shear near the qmin point is associated with stronger local shear on the outboard side. Geometric effects such as shaping and Shafranov shift can strongly increase these effects further. Secondly, higher β increases electromagnetic effects in the turbulence. It is important to assess behavior with electron heating, which further changes the character of the turbulence (favoring lower k ITG and TEM modes) in ways expected for burning plasma devices. The DIII-D program has made significant progress in assessing these issues, finding favorable transport properties for high β regimes.
Effect of Current Profile
While turbulent transport is known to generally degrade as the electron-to-ion temperature ratio increases from below 1 to near unity [97], recent experiments in steady-state scenario plasmas on DIII-D have shown that negative central magnetic shear (NCS) mitigates the transport degradation observed during electron cyclotron heating [98]. In these studies, systematic comparisons are made of core turbulence and transport at high Te/Ti as the magnetic shear is varied by adjusting the early heating power, plasma current ramp rate and L–H transition time. For plasmas with positive magnetic shear (PS), both the ion and electron thermal diffusivities increase by ≈ 3 × near the mid-radius when Te/Ti is raised from 0.8 to 1.1. Both the ion and electron thermal transport increase less with higher Te/Ti for NCS plasmas, and the drop in H98y2 during ECH is also significantly smaller (5% vs. 18%) for NCS plasmas compared to PS plasmas. The Te/Ti dependence of transport observed on DIII-D is consistent with that observed on JT-60U, but the DIII-D studies permit deeper investigation of the underlying physics [99].
These DIII-D experiments have provided a more comprehensive physics understanding of the transport dependence at high Te/Ti between positive and negative magnetic shear through measurements of the plasma turbulence. As seen in Fig. 21, the low-k broadband turbulent fluctuations increase less in NCS plasmas compared to PS plasmas with increased Te/Ti [98]. Furthermore, a clear difference in the behaviour of low-k and intermediate-k fluctuations is seen, with low-k electron temperature fluctuations at ρ ~ 0.6 increasing with electron heating in NCS plasmas and intermediate-k electron density fluctuations around ρ = 0.65–0.7 decreasing with higher Te/Ti in both PS and NCS plasmas. Linear simulations using the GKV electromagnetic gyrokinetic Vlasov code find that the growth rates of low and higher-k modes increase less with electron heating for NCS plasmas than for PS plasmas, and the dominant mode switches from ITG to TEM in the PS region as Te/Ti is increased. These experimental and theoretical results encourage the development of Advanced Tokamak scenarios with NCS current profiles to mitigate the increase in thermal transport at higher Te/Ti.
To understand the effect of q profile on bootstrap fraction, systematic scans of the current profile in DIII-D, were made using an off-axis injecting neutral beam installed in 2011. These revealed that the ion and electron thermal diffusivities scale differently with the q profile [100]. As seen in Fig. 22, the electron heat channel improved with higher qmin, whereas more power was expelled through the ion channel as qmin increased. As a consequence, confinement did not improve with higher qmin values. These core transport experimental trends did not seem to match well with the TGLF model, which fits linear turbulent modes to predicted saturation levels from the GYRO non-linear code. Far infrared (FIR) chord integral fluctuation measurements showed low-k density fluctuations rising as qmin rose. The effects of this ion transport degradation on the profiles was observed to impact the bootstrap and non-inductive current fractions achievable for each type of q profile. In addition, higher q95 was found to lower pedestal height, while higher qmin was found to raise core temperatures and broaden profiles. Thus, the maximum bootstrap fraction is not found at the maximum qmin as expected.
These observations highlight the importance of deeper investigation of transport dependencies to resolve physics models and map the path to high performance fully non-inductive operation, motivating upgrades to DIII-D to increase current profile flexibility, as discussed in section "Future Research Requirements and DIII-D’s Role".
Effect of High β
Reaching high bootstrap fraction fully non-inductive plasmas, requires operation at high poloidal beta, βP, the pressure relative to poloidal field. This has a natural synergy with transport optimization as high βP increases local shear, stabilizing turbulence. Recent experiments on DIII-D show an internal transport barrier (ITB) spontaneously forms [37] with high bootstrap current leading to improved energy confinement. This is largely a result of turbulence suppression from a large outward shift of the core plasma that increases the local magnetic shear on the outboard ballooning side of the plasma.
Using both gyrokinetic stability analysis and quasi-linear turbulent transport predictive modeling [101], it is found that plasma discharges with high bootstrap fraction can self-organize into a state with either a strong internal transport barrier (ITB) and a weak edge transport barrier (ETB), or a weak ITB with a strong ETB. The weak ITB state can be triggered to switch into a state with a strong ITB state by its large edge localized modes (called ELMs). The strong ITB type is more persistent due to its smaller ELMs. Both types of discharges show improved energy confinement over the standard ITER98pb(y,2) scaling by up to 80%. However, it is noteworthy that discharges with the strong ITB achieve the highest energy confinement. Transport differences between the two discharges are partially controlled by the kinetic ballooning mode instability (KBM). Thus self-organization occurs by interactions between the bootstrap current, magnetic shear, and the KBM stability, while at lower bootstrap fraction the ITB collapses and the energy confinement drops (Fig. 23). It should be noted that even these smaller ELMs are unlikely to be sufficiently small for ITER, and almost certainly not for a fusion reactor, where the steady state exhaust is already a major challenge. Thus ELM control development for steady state regime remains essential,
A deeper analysis of these discharges [102] reveals the electron transport in the core to be enhanced by electromagnetic effects that develop at high β and multiscale effects. The importance of including these effects is highlighted in Fig. 24, where DIII-D data [73] is compared with transport models using either only electrostatic or also electromagnetic effects. In the electromagnetic simulations it is found that ion scale turbulence suppresses electron scale fluctuations due to zonal flow mixing. A new saturation model in TGLF that incorporated this effect improved accuracy of temperature predictions, with the electromagnetic effects reducing temperature gradients, to achieve a better match to experiment as shown in Fig. 24 [74]. These effects, and discrepancies with experiment become more pronounced at higher q95; there is clearly much further work to do to resolve transport models for high β advanced tokamak plasma configurations. Not least direct perturbative measurement of fluctuations in relevant configurations could directly validate the processes involved. And, as we set out in section "Burning Plasma Relevant Conditions", increases in ECH and current drive capability will permit exploration of this physics in more reactor relevant dominantly electron heated steady state regimes.
Stability
From the viewpoint of MHD stability, the greatest difference between steady state advanced tokamak scenarios and more conventional scenarios is that most AT scenarios operate at high normalized beta (βN), requiring a nearby (distance ~ 30–40% of minor radius) conducting wall for stability to long wavelength kink modes. The steady state hybrid scenario typically is very near the no-wall, ideal-MHD stability limit [45, 51], while the high-qmin and high-βP scenarios significantly exceed it [41, 103]. Only the high-ℓi scenario [48] achieves high βN without wall stabilization. The broad profiles of pressure and current density that are preferred for maximizing the bootstrap current are in addition favorable for wall stabilization, and DIII-D’s off-axis neutral beam injection (a capability added in 2011) contributes to broadening of these profiles [40, 50, 100]. As shown by the blue data points in Fig. 25, high-qmin advanced tokamak discharges in DIII-D often significantly exceed the no-wall stability limit, indicating the influence of wall stabilization [68].In the case of a real wall with finite conductivity, the ideal kink mode is predicted not to be fully stabilized, but instead is converted to a resistive wall mode (RWM) with a growth rate and real frequency of the order of the inverse resistive time of the wall. In high-qmin experiments, for example, slowly growing instabilities consistent with the RWM are often observed to cause beta collapse or termination of the discharge at high βN, as indicated by the yellow points in Fig. 25. Understanding the conditions for “passive” stability of the RWM above the simple ideal-MHD, no-wall limit has been an important challenge for AT research.
50 ms time-averages of experimentally accessed βN (thermal + fast ion) versus ℓi values, with (squares) and without (circles) RWM feedback control, including β-collapses due to n = 1 RWM events (triangles), and no-wall (dashed curve) and ideal-wall (dottedcurve) ideal MHD βN limits obtained from scaled experimental equilibria. [From J.M. Hanson, et al., Nucl. Fusion 57, 056009 (2017)]
A key development of the past decade has been the prediction and experimental confirmation of the role of kinetic damping in the stability of the RWM, superseding earlier models of RWM damping that invoked sound waves or Landau damping. The passive stability of the RWM at high βN is now understood to result from resonant wave-particle interactions [104,105,106], including the transit frequency of passing particles as well as the bounce and precession frequencies of trapped particles. The plasma’s ExB flow Doppler-shifts these frequencies into resonance with the near-zero frequency of the RWM. In a DIII-D experiment [107] that actively probed the stability of the mode, the RWM was excited with a 20 Hz magnetic perturbation while the plasma rotation was varied using the neutral beam torque. The measured amplitude and phase of the plasma response agree well with the predictions of the MISK model [106] (Fig. 26). The two minima in the amplitude, indicating stronger damping of the stable mode, are attributed to resonant damping at the precession drift frequency and the bounce frequency of trapped ions. Other MISK calculations show that the passively stable points above the no-wall limit in Fig. 25 are consistent with stabilization by kinetic damping [68].
Comparison of the measured (squares) and modeled (line) rotation dependence of the a amplitude and b toroidal phase shift of the plasma response to a slowly rotating externally applied n = 1 field. The plasma response δBplasr is measured with radial field sensors, the external field is applied with the I coil, and the ωE rotation is normalized with τ−1A and evaluated at q = 2. [From H. Reimerdes, et al., Phys. Rev. Lett. 106, 215002 (2011)]
Reducing the plasma-wall distance can also improve wall stabilization. In high-βP experiments in DIII-D, ELMs are found to trigger a transient n = 1 external kink that leads to a temporary collapse of the H-mode edge pedestal or a disruption [37]. The kink and the ELM that drives it both typically evolve on a sub-millisecond time scale, shorter than the time constant of the vessel wall, and thus the instability behaves as an ideal-wall kink mode. Reducing the plasma-wall distance improves the stability of the discharge, consistent with ideal-MHD stability calculations using GATO [37, 70].
Active feedback stabilization of the RWM can extend the regime of stable operation very close to the ułtimate limit of ideal-wall stability boundary. Active stabilization of the n = 1 RWM was applied to some of the high-qmin discharges in Fig. 25, using simple proportional gain with internal non-axisymmetric control coils and internal poloidal field sensors. As shown by the magenta points, active stabilization yields a significant extension of the stabilized regime to higher βN [68]. Some of the RWM instabilities that occur during feedback control are the result of an unstable n = 2 RWM, which was not addressed by the control scheme. Other DIII-D experiments to measure the stable plasma response [108, 109] have shown that multiple n = 1 and n = 2 modes may be excited at high βN near the no-wall limit. These observations indicate that multi-mode feedback control is a frontier for future development.
Advanced state-space control algorithms can improve the robustness of a feedback system by improved filtering of noise and disturbances [110], and have been employed in NSTX [111] to extend the range of stabilized operation to higher βN and βN/ℓi. A linear quadratic Gaussian (LQG) controller was developed and tested in DIII-D. Initial results show that the LQG controller is more efficient than simple proportional control in suppressing an “artificial RWM” magnetic field pattern created by other coils. Notably, its performance in maintaining stability above the no-wall limit using more reactor relevant external control coils matched that of a proportional gain controller using internal coils—a significant development [112]. This suggests that with further work, it may be possible to translate the learning and physics advances being developed with internal coils, as discussed above, to practical reactor relevant external coils.
AT plasmas are also subject to tearing modes, which often become the performance-limiting instability when kink modes are avoided using the strategies discussed above. In steady-state hybrid discharges, resistive modeling with DCON and PEST3 predicts improved stability to tearing modes with broader current density and pressure profiles [44]. In such discharges, a “flux pumping” dynamo process maintains a broad current density profile and also reduces or eliminates sawteeth as seeding events for neoclassical tearing modes (NTMs), both contributing to better stability against m/n = 2/1 NTMs than for conventional H-mode discharges [45, 51]. In high-qmin discharges above the no-wall stability limit, tearing stability is closely linked to the approach to ideal-MHD stability limits. Broadening the pressure and current density profiles is predicted to improve both ideal and resistive stability limits [100]. Off-axis electron cyclotron current drive (ECCD) is found to improve stability to the 2/1 tearing mode, but insensitivity to the exact radial location indicates that the mechanism is likely to be modification of the tearing stability index ∆′ rather than direct stabilization by localized current drive at the q = 2 surface [100, 113]. Raising qmin above 2 eliminates the 2/1 tearing mode, but 3/1 modes can still occur [68]. High-ℓi discharges are also often limited by 2/1 tearing modes. As in the high-qmin case, pre-emptive ECCD near the q = 2 surface helps to avoid 2/1 modes, again probably through modification of profiles and not direct stabilization [48].
Remaining challenges for the stability of AT scenarios include the validation of kinetic damping models in the various specific AT scenarios, particularly at higher βN and at low rotation, and with decreased energetic particle fraction. The development and validation of state-space controllers, including multi-mode control, will improve stability while minimizing the control power. The capabilities of RWM stabilization with external coils should be pursued. Tearing modes remain a significant issue for most scenarios, and the challenge is to develop capabilities of stability prediction and profile control that will enable confident design and operation of passively stable discharges.
Energetic Particle Physics
Energetic particles (EP) provided by the eight 80 kV neutral beams in DIII-D play critical roles in heating, current drive, momentum input and plasma stability, enabling critical studies of these interactions. The presence of these energetic particles introduces challenges as these particles can excite a variety of Alfvén eigenmodes (AE) and other instabilities, which in turn can lead to a range of transport mechanisms and other effects. The resultant fast ion transport and loss can reduce performance, redistribute currents or cause localized heating and damage of first wall components. AT scenarios on DIII-D can have high fast ion content (βfast/βtotal) up to 40% and are often observed to have a variety of unstable energetic particle driven instabilities which limit the achievable performance. Several scenarios are typified by reversed or broad/weakly reversed magnetic shear with relatively high qmin. These scenarios are particularly susceptible to Alfvén eigenmode activity and are the focus of this section.
Transport of Energetic Particles and Predictive Tools
Neutral beam injection into reversed magnetic shear DIII-D plasmas, like those characteristic of various AT scenarios, produces a variety of Alfvénic activity including toroidicity induced Alfvén eigenmodes (TAE) [114], reversed shear Alfvén eigenmodes (RSAE) [115, 116], ellipticity induced Alfvén eigenmodes (EAE) [117], beta induced Alfvén eigenmodes [118], beta induced Alfvén acoustic eigenmodes (BAAEs) [119], and linearly coupled RSAEs and TAEs [120]. By studying these modes during the discharge current ramp phase, when incomplete current penetration results in a high central safety factor and strong drive due to enhanced coupling to multiple higher order resonances [121], a great deal has been learned about the physics of the eigenmodes and their impact on fusion plasmas.
Work in this area has progressed rapidly due in large part to advances in diagnostics for both fast ions and the eigenmodes themselves. For example, measurements of the confined fast ion profile are now routinely available from Fast Ion Dα measurements FIDA [122] and full eigenmode structures are routinely measured by Electron Cyclotron Emission (ECE) [123, 124]. Many of the predictions for linear properties of the typical eigenmodes mentioned above have been observed experimentally and are now well understood. An example is shown in Fig. 27, where ECE measurements as well as ideal MHD predictions from the NOVA [125] code for RSAEs and TAEs are given [120]. The RSAEs are clearly localized near qmin and the TAEs are seen for radii outside of qmin extending to the plasma edge. These are the most common Alfvén eigenmodes modes observed in DIII-D AT plasmas. The NOVA results shown here exhibit close agreement with the measured spatial structure of the temperature perturbation for both the n = 3 RSAE and TAE, including the oscillatory structure of the solutions in the radial direction, and predicted mode frequencies were within 10% of calculations.

Adapted from [124]
Discharge 122,117, t = 410.6 ms. a Radial profile of ECE radiometer power spectra. RSAEs (blue line) and TAEs (red line) are pointed out along with toroidal mode number (n). b, c Diamonds = ECE radiometer measured temperature perturbation; solid line = NOVA prediction for ECE radiometer temperature perturbation. Eigenmode amplitude scale factor obtained by least squares fit to the ECE data.
Data from fast ion diagnostics on several devices worldwide indicate that during periods of strong Alfvénic activity the central fast ion population is significantly depleted relative to expectations based on neoclassical diffusion alone [126]. An example of the observed fast ion profile flattening is shown in Fig. 28, where the fast ion pressure profile inferred from equilibrium reconstructions is given along with FIDA measurements and the classical TRANSP prediction [126]. Throughout this time period the neutron rate is approximately 50% of that predicted by TRANSP, but consistent with a large radial transport of the beam ions (DB = 5 m2/s, inset). In addition to impacting heating, torque and overall performance, this large transport has been shown to have a similar effect on the neutral beam current drive (NBCD) profile, something which can have serious implications for steady-state scenario development [62, 126,127,128]. Interestingly, there are examples where EP instability induced fast ion transport was actually found to benefit performance by redistributing central NBCD causing a reduction in central magnetic shear and the formation of an internal transport barrier [127]. Subsequent fast ion transport experiments have identified critical gradient-like or stiff behavior of the fast ion profile where above a phase space dependent threshold, EP transport rises sharply [62, 129]. An example is shown in Fig. 29, where measured FIDA profiles become clamped above a critical beam power due to an increasing level of Alfvén eigenmode activity (not shown), and the measured neutron deficit (panel b) is found to increase abruptly from classical levels above ~ 3 MW injected power.

Adapted from [126]
a Experimental (solid) and TRANSP modeled (dotted) fast ion pressure profile in discharge 122,117 at t = 365 ms. Experimental fast ion pressure profile is obtained from EFIT reconstructions subtracting off the measured thermal pressure from the total pressure. Data points are FIDA measurements. b TRANSP estimates for fast ion pressure with and without central beam ion diffusivity (profile shown in inset).

Adapted from [62]
a Discharges dominated by RSAEs near mid-radius and TAEs extending to edge. Fast-ion transport measured with FIDA is localized to the midcore radii as beam power increases. At increasingly high beam powers, FIDA density profiles are unchanged. b Time-averaged divergence of modulated flux, i.e.,transport, inferred from the neutron emission.
This large deficit in the central fast ion population is a common feature of discharges with multiple Alfvén eigenmodes and has generated both concern and interest worldwide. In 2010, the EP deficit in DIII-D was explained using guiding center calculations in the presence of a spectrum of modes [130, 131] using the ORBIT code [132] and mode structures from the ideal MHD code NOVA, matched to experiment. It was found that the measured mode amplitudes were just above the threshold for stochastic transport due overlap of multiple wave particle resonances of the central fast ion population. This was well described in self-consistent coupled mode-EP simulations (Fig. 30) [133,134,135].

Adapted from [135]
MEGA simulations of DIII-D plasmas showing: a Central fast ion density resulting from a range of injected neutral beam powers with (solid) and without (dashed) Alfvén wave physics included. b, c Show ion orbit perturbations due to individual wave-particle resonances in the 1.56 MW and 15.6 MW cases.
EP Behavior in AT Scenarios
AT scenarios with elevated q profiles like those discussed above, are more susceptible to EP driven instabilities and fast ion transport. The reason is two-fold. First, elevated qmin allows fast ions to drive energetic particle instabilities more effectively through higher order resonances [121, 130, 136]. These are particularly important in DIII-D plasmas, since the 80 keV beam energies are not able to fulfill the fundamental wave-particle resonance condition at normal operation fields. Second, scenarios with elevated qmin often have weak or reversed magnetic shear, and these types of q-profiles result in wider modes with weaker continuum interaction that are capable of interacting with the energetic particle population over a larger radial range. At even weaker poloidal field like that in DIII-D high-βP discharges, fast ion loss boundaries can be present in the core of the plasma and allow energetic particles to be lost to the vessel wall [41, 137].
Figure 31 compares the q-profiles obtained during the high-βN phases of a pair of consecutive AT discharges. Both use the same boundary shape and have density profiles with the same shape, but the qmin~ 2 case is approximately 10% lower density at all radii. The crosspower density fluctuation spectra between the two most central interferometer chords shows significantly more TAE activity in the plasma with qmin ~ 2 than qmin ~ 1, with average amplitude of coherent modes in the TAE band about four times higher. These cause additional transport of energetic particles, with plastic scintillator neutron counts 43% lower and a 17% energy deficit relative to TRANSP predictions (panel b), typical for such high qmin AT plasmas. [138, 139].

Adapted from data presented in [61]
a Safety factor profiles during the high-BN phase of two discharges. b Stored energy deficit between classical expectations and measured. c, d Cross-power density fluctuation spectra versus time from CO2 interferometer chords showing AEs for the c high-qmin case and d low-qmin case. The solid white lines denote the TAE frequency at the magnetic axis.
High βP scenarios like those discussed in section "High βP Scenario" are also susceptible to EP driven instabilities and fast ion transport. For example Fig. 32 shows that the diffusivity level required to match the measured neutron emission roughly tracks the AE mode activity. As the density increases, the fast ion slowing down time decreases, reducing fast ion content (thereby reducing the AE instability drive), and the distances travelled by displaced fast ions before thermalization. Both effects lead to reduced fast ion losses. Calculations of the Alfvén continuum indicate that during the high density phase, the core TAE gap is relatively closed [139], which may also contribute to the reduced AE activity and resulting lower fast ion transport [37].

Adapted from data presented in [37]
Discharge 154,406. Time histories of: a combined frequency spectra of line-integrated density fluctuations from four separate CO2 interferometer chords; b measured and calculated neutron rate (calculations are carried out using different values of the spatially uniform beam-ion diffusion coefficient DB, color coded); c value of DB required to match the measured neutron rate; d line averaged electron density, pedestal density, and NBI power.
It should be noted that other scenarios such as steady-state hybrid plasmas (with qmin~ 1–1.3) are also susceptible to EP transport, and, depending on qmin, they can have either AEs or Fishbones that cause significant transport and limit performance [51].
Potential for Control or Avoidance of AEs to Improve AT Scenarios
Comparison of cases with high and low fast ion transport has suggested ways to improve the qmin ~ 2 scenario [63] that the DIII-D EP program has begun to explore experimentally. For example, if the negative magnetic shear region can be expanded so that the qmin radius is moved outwards where there are fewer fast-ions, then the drive of RSAEs (and perhaps other EP modes) should be greatly reduced, as shown in Fig. 33, to suppress the core TAEs [63, 140]. Also, the drive for AEs can be altered by varying the radial gradient in the fast ion pressure profile grad-βfast [129, 136] to keep it below a critical threshold [139] through variation of density and NBI power as well as NBI injection geometry. In 2010, two beams on DIII-D were modified to allow off-axis injection as opposed to central deposition. The result is the capability to create flat or potentially off-axis peaks in the fast ion pressure profile and thus completely stabilize the RSAEs (Fig. 34). At the beginning of the 2019 DIII-D experimental campaign, the amount of off-axis NBI power available to DIII-D will be doubled, allowing the exploration of high qmin AT scenarios with broader, more stable beam ion profiles. To the extent that neutral beams or other externally controllable sources of fast ions such as ICRH tail acceleration are available in a fusion power plant, the potential will exist for tailoring of the fast ion profile to reduce (or possibly enhance) fast ion transport and optimize performance. The actual 3.5 MeV alpha fusion product profile, however, will be more difficult to control directly and may ultimately drive instabilities that limit performance.

Adapted from data presented in [63]
Graphical depiction of High-Betap scenario and improved resilience to AE induced EP transport.

Adapted from [129]
Core TAEs occur inside of qmin where the fast-ion profile is flat or hollow with off-axis injection, RSAEs occur near qmin where grad (βfast) is small during off-axis injection, and global TAEs lie in a region where the gradient is insensitive to changes between on-axis and off-axis injection. The illustrated fast-ion profiles are from classical calculations performed prior to the experiment. b, c Crosspower of adjacent ECE channels that are located near qmin during b on-axis and c off-axis injection. The same logarithmic color scale is used in both figures. In the off-axis case, the mode activity at 400 and 500 ms coincides with brief diagnostic blips of the on-axis beams.
Experiments carried out on DIII-D also show that localized electron cyclotron heating (ECH) can drastically alter beam driven AE activity including, in some cases, the stabilization of RSAEs and improve fast ion confinement [64, 141, 142]. Similar experiments have been carried out on several devices, altering AE activity in Heliotron J [143] the TJ-II stellarators [144] and on ASDEX Upgrade [145]. The suppression occurs when ECH is deposited near qmin in DIII-D experiments (Fig. 35), when only the very end of RSAE chirps are visible.

Taken from [142]
a Representative equilibrium overlayed with ECH ray trajectories for heating near qmin (II) and near the axis (I). b #128564, Crosspower spectrum of vertical and radial interferometer showing RSAE activity during ECH deposition near axis. Typical RSAE frequency evolution highlighted at t ~ 550 ms. c #128,560, Spectrum showing lack of RSAE activity during ECH deposition near qmin. Same color scale is used for b and c.
In 2017, an engineering upgrade to the neutral beam system on DIII-D enabled time-dependent programming of both the beam voltage and current [65, 66]. This has enabled the injected beam ion population to evolve with plasma characteristics in order to navigate the AE space, to optimize heating and AE stability in real time, and thus discharge performance [66]. This raises the exciting prospect of exploring how to tune EP populations with subtle changes to manage the plasma EP stability.
Future Research Requirements and DIII-D’s Role
Considerable further research is needed to establish the physics basis for the AT approach and determine the design choices of a steady state fusion reactor. DIII-D capabilities for fully non-inductive operation have been limited so far to quite modest βN levels (up to ~ 3) and profiles, with transient explorations at somewhat higher performance regimes. Understanding how the plasma will behave in actual reactor-like plasma configurations is key to projecting the hardware requirements, size and design of such a reactor. Viable approaches must be developed if one is to move to a decision to construct, and indeed know how to specify that design. Most importantly, it is critical to understand how to reach a self-consistent solution—both within the core, and in terms of compatibility with a divertor and wall solution. This is a central focus of DIII-D’s ongoing research [52]. It is also important to explore the technological and engineering approaches for a steady state fusion reactor, though we leave this aspect to other papers, focusing here on the plasma research that sets the scale of the challenges faced by those systems.
International Context
New plasma research capabilities are needed to resolve the path to a steady state fusion reactor. Many devices around the world exploit co-injected neutral beams to reach high performance, heating the ions and driving favorable rotation, unlike in a fusion reactor. The push to operate with reactor relevant wall materials, though important to study, has forced facilities to high collisionality, as they use gas puffing to drive ELMs to flush impurities from the core; on present scale devices, this forces the pedestal to the reactor-irrelevant ballooning limited part of the operational space, and the core to elevated collisionality [146]. Flexibility to access high βN and vary current and pressure profiles is also limited, while reactor compatible current drive tools (which must be more efficient than present technologies, and solve antenna loading and plasma facing component issues) have yet to be developed. The world’s facilities are well suited to explore improved divertor concepts with the highly flexible MAST-U and beam-upgraded TCV facilities coming on line in 2018, and tungsten divertors on JET, ASDEX Upgrade and WEST (where the divertor can be heated). However, integration of closed divertor approaches with high performance fully non-inductive cores remains elusive.
Further developments are planned in the near term that can address key elements of this challenge. In particular:
-
The superconducting EAST and KSTAR facilities can operate high βP regimes for long pulses, although are limited in absolute performance or βT. Key opportunities include assessment of long pulse control technologies and long time scale wall evolution [147]. In collaboration with these devices, DIII-D uses its flexibility to scope out high βP regimes and understand the physics basis, prior to long pulse testing.
-
JT-60SA will be a key facility to test projections to larger scale. It begins operation in lower single null as an ITER-satellite. As heating power develops, high performance AT operation becomes possible at reduced field and current, while a later extended research phase is proposed with a double null ‘advanced’ divertor [148].
-
JET and ASDEX Upgrade facilities have focused on the influence of metal walls on plasma operating scenarios, concentrating in particular on the ITER baseline and inductive paths. Nevertheless, ASDEX upgrade has recently shown compatibility of Tungsten walls with moderately advanced tokamak regime through strong core electron heating and careful heat load management strategies to overcome impurity accumulation [149, 150]. This opens up an important vein of research explore compatibility of AT scenarios with reactor like walls.
In this context, the DIII-D facility focuses on exploring the core advanced tokamak physics and its compatibility with reactor relevant plasma exhaust solutions. On the core it will exploit its high configuration flexibility to develop reactor relevant scenarios and resolve scientific questions. In parallel it is assessing improved divertor concepts and underlying divertor physics to project how to detach plasma exhaust from plasma facing components while maintaining AT configurations.
DIII-D Plans
The DIII-D facility is now being redeveloped to access regimes at reactor like physics parameters and plasma configurations directly, in order to address the relevant physics at the performance levels required and resolve the techniques needed for future fusion reactors. Starting in 2018, major improvements in current drive tools, electron heating, 3D fields and divertors are foreseen, providing capabilities that will complement those elsewhere around the world. The below described elements represent a coherent package of facility developments proposed for the next DIII-D operating period from 2019 to 2024. Further gaps to a fusion reactor, facility potential and more speculative long term possibilities are reserved to a discussion in section "Further Gap Issues to Fusion Reactors".
Fully Non-inductive Steady State Regimes
A foundational element of the steady state approach is to demonstrate that self-consistent fully non-inductive solutions can be sustained at required performance levels, and to understand what the performance limits and required control tools are. DIII-D is being upgraded with large rises in flexibly deposited current drive and increases in available heating power to access the full range of potential high β steady state reactor configurations to determine the path and the physics basis. It is also pioneering new current drive technologies to proof out the tools that will be required in a steady state fusion reactor.
In 2018, DIII-D neutral beam systems will be re-oriented to double off-axis current drive power. Two of the 8 beams will be toroidally steerable, allowing all power to be injected in the plasma current direction to assess high βN limits, as well as enabling rotation variation at lower current drive levels. Beam energy rises will increase current drive and electron heating. This will be augmented by increases to 9 MW electron cyclotron current drive power, to be used to finely tune the current profile for performance and stability control thanks to its precise deposition control.
These developments will broaden current profiles and remove rational q flux surfaces (Fig. 36) to access projected-stable configurations. Simulations predict transport and stability limits will rise to reach βN ~ 5 fully non-inductively (Table 2), comparable to ARIES-AT parameters, with flexibility to explore the roles of current, pressure and fast ion profile, with modeled solutions ranging from peaked current so-called ‘high li’ scenarios, to the broad current ‘high qmin’ shown here. This will enable tests of (1) kinetic damping and resistive MHD close to ideal MHD β limits, (2) probing and control of energetic particle driven instabilities, (3) assessment of the role of current profile in high β electromagnetically driven turbulence, and (4) compatibility of advanced profiles with fully non-inductive sustainment and performance limiting physics.
DIII-D will also assess the physics of three promising new current drive technologies, which simulations indicate could lead to much greater efficiency in future reactors, also addressing coupling and antenna issues—potential game changers in required scale and performance of the device. These are top launch ECCD, ultra-high harmonic fast wave (Helicon) [151, 152], and high-field side lower hybrid current drive (HFS LHCD) [153]. Helicon has, in fact, already demonstrated good coupling in low power tests on DIII-D [152] and is proceeding to a 1 MW installation in 2019, alongside proof of principle top launch ECCD tests. HFS LHCD is planned soon after. Projections indicate these could substantially improve current drive and further broaden profiles on DIII-D (Fig. 37) to further study transport, stability and energetic particle physics, raising ideal MHD βN limits to values approaching 6, and thereby fostering potentially more robust margins for ideal and resistive MHD stability.
This work will establish the potential for fully non-inductive high βN scenarios with stationary current and pressure distributions that are consistent with current drive sources, and macroscopic and Alfvénic stability.
Burning Plasma Relevant Conditions
The critical further step in developing a steady state core is to project regimes to burning plasma conditions. Rotation, collisionality, Te/Ti and energetic particle content all play crucial roles in determining the structure, magnitude and channels of turbulent transport, modifying fluctuations from fine scale instabilities to large structures (Fig. 38), and altering pinch and diffusive effects. These parameters are also critical determinants of ideal MHD βN limits through kinetic resonances with plasma rotation and energetic particle interactions [107]. Collisionality and rotation can further play important roles in pedestal stability and height.
To address these issues DIII-D plans progressive increases in electron and torque-free heating. A second pair of beams will be made toroidally steer able to enable full-power balanced torque operation. Combining with the planned upgrade to 9 MW ECH, which increases electron heating and current drive, simulations predict this will enable fully non-inductive plasmas with advanced tokamak profiles (Fig. 39 with qmin > 1.5) and burning plasma relevant parameters (Te/Ti ≈ 1, low ν* and rotational shear) at βN ~ 4 and q95 = 6. Additional helicon or HFS LHCD improves on this further, replacing lost neutral beam current drive with further off-axis currents to study the influence of advanced tokamak profiles on transport and stability up to βN ~ 5 in torque free H-modes (Fig. 40). The increased ECH also permits evaluation of reactor relevant dominant electron heating and thus burning plasma transport processes at low rotation in these regimes. Separately, these current drive tools enable operation at higher density to study coupled electron–ion turbulence at Te ~ Ti and zero torque.
This will enable development of validated models to predict burning plasma performance, with assessments of how these parameters impact critical gradients for drift wave induced turbulent transport in all channels. Research will evaluate how scenarios can be adapted to loss of ExB shear stabilization, and how optimization of the magnetic shear profile may be used to compensate. ECH will also enable precise perturbative tests of turbulence and pedestal behavior. Kinetic MHD stabilization physics will be advanced by varying the influence of fast ions using variable beam geometry, voltage, and by increasing βthermal/βfast using ECH.
Control of Instabilities and ELMs
Sustained operation of tokamak fusion plasmas requires control and mitigation of deleterious transient events. Plasma instabilities, including edge-localized modes (ELMs) and core, tearing, or global instabilities that lead to disruptions, could prevent reactors achieving their mission through damage to the facility or de-rated operation to avoid potential damage.
The heating and current drive tools discussed in section "Fully Non-inductive Steady State Regimes" will be highly important in exploring and understanding how to stabilize instabilities. One aspect is to assess the physics and develop control of global plasma stability at high βN, where kinetic stabilization mediates a dissipative interaction of the pressure driven kink with the resistive wall, into which the broader current profiles achievable will that displace the eigenmodes more deeply. Toroidally steerable, variable-voltage neutral beams and ECH will also vary ion velocity distribution and rotation to explore the resonant interaction of this mode with orbital frequencies of trapped ions behind this kinetic damping effect.
A second crucial aspect will be the understanding of tearing mode influence, where even with the 2/1 surface removed, there remain concerns over the incidence of higher m/n modes (5/2, 3/1). Are these a manifestation of proximity to ideal MHD limits, or likely to occur more broadly across the operating space? If the latter, can current drive techniques be developed to maintain passive stability or actively remove modes when they occur? Exploring the high βN stability space will be a crucial research goal, benefiting from both the broad regime access and the local perturbative capabilities with ECCD.
A further critical element is the use of 3-D fields to control instabilities such as ELMs, where significant progress has been made on DIII-D. However, present capabilities have limited harmonic flexibility to toroidal mode numbers of n = 1 or 2, whereas the optimal fields for ELM and rotation control have n = 3 or 4. Simulations developed [D.W. Weisberg et al., in preparation, 2018] in the DIII-D program predict that at these higher n it will be possible to vary the plasma response to independently control interactions in different parts of the plasma, thus controlling rotation profile, locked modes and ELMs independently. These simulations predict that much more efficient coil sets for 3-D control are possible. A projected 12 coil midplane (‘M’) array (Figs. 41, 42) will test this physics, providing the first detailed spectral optimization studies for ELM and rotation control with n = 3 or 4 fields. This will help understand how best to deploy 3-D field configurations to control ELMs and minimize hot spots for steady state fusion reactors, where such techniques are likely to require coils to be located outside the vessel for protection. The approach here is to exploit DIII-D flexibility to resolve the physics of the interaction and understand the optimization, so that a simplified external coil approach can be developed for a fusion power plant. This coil set will also help understand the optimization for ITER, which has a coil arrays that the new DIII-D set would closely emulate.
This enhanced 3-D coil set coupled with upgraded 3-D diagnostics will also be able to probe the plasma response to applied field in order to measure RWM dissipation physics at n up to 6, and develop advanced active control techniques at βN approaching the ideal-wall limit (Fig. 25) to project a path to high βN ideal MHD stable operation.
Should reactor systems fail, safe means to quench a fusion plasma are needed. Present techniques inject particles at the edge, limiting assimilation and allowing dangerous runaway electron beams to grow. DIII-D plans to develop ‘inside-out’ disruption mitigation using low-Z shell pellets filled with dust to deposit particles to the core. Modeling (Fig. 43 [156]) indicates this will dramatically improve all aspects of the disruption: 100% impurity assimilation assures high radiation fraction for rapid thermal quench; decay of the plasma current occurs more slowly (reducing induced forces) due to a still-warm plasma edge, while stochasticity generated in the core dissipates incipient runaway electrons. Particle and radiative diagnostics will be deployed to validate models of the quench and runaway dissipation, to develop predictive understanding.
Core–Edge Integration
A fundamental issue for a steady state reactor is to find a solution that simultaneously delivers high core performance and has compatibility with the divertor and wall. Fusion reactor cores will operate at low collisionality, ν*, due to their high field and current [ν* ~ ne/(I2P B2T shaping2) ~ n3e /P2], while divertor protection requires a high absolute density dissipative divertor with a high degree of radiation to spread heat and reduce particle energies; a state known as ‘detachment’ This must also provide sufficient pumping for helium ash removal and steady-state density maintenance. However, such dissipative techniques and wall interactions can lead to neutral and impurity influxes that adversely affect the core and pedestal performance. Conversely, access to high power low collisionality cores can lead to divertor and wall fluxes that are particularly challenging to deal with.
Part of the solution is to alleviate this tension by improving behavior in each region. For instance, closed divertors, such as the promising ‘small angle slot’ (SAS) configuration [H. Guo et al., in preparation], would facilitate detachment at lower upstream density, with neutral dynamics optimized to reduce particle energies at all radii (Fig. 44) and somewhat trap neutrals in the divertor region to reduce core fueling), while simultaneously controlling heat flux and erosion—a great challenge facing steady-state fusion reactors. Alternately, a super-H mode pedestal raises pressure (noting ν*ped ~ n3e /P2) to achieve a high density, low ν* pedestal solution [157] that may facilitate high density divertor detachment access. Planned power upgrades and increased PF shaping flexibility will help explore such optimizations and the interactions between the two regions. Further, planned installation of more closed configurations in both the main upper and lower pumped divertors will enable investigation of higher density detached states at high power and particle flux with increased neutral and photon opacity compared to present capabilities, in order to explore the interaction of detached radiating divertor regimes with both divertor geometry and the plasma core.
Core–edge interactions will be explored through new profile, turbulence and neutrals diagnostics, exploiting relevant low ν* access to assess governing pedestal physics. Compatibility and interaction of impurities arising from the wall and radiative mantle techniques with core performance will be assessed, utilizing perturbative impurity transport techniques, facilitated by a new laser blow off system and a hot tile test facility, as well as changes to wall and divertor materials. Siliconization and a subsequent SiC main wall tile arrays will provide a low carbon environment to assess impurity and radiative divertor dynamics, as well as a potentially interesting candidate reactor wall material. The planned helicon and HFS LHCD upgrades discussed in section "Fully Non-inductive Steady State Regimes" are also projected to enable higher density variants of the fully non-inductive βN ~ 5 plasmas discussed earlier to assess core-divertor solutions (Fig. 45).
Further Gap Issues to Fusion Reactors
The capabilities discussed above will position DIII-D well to validate physics models and develop technical solutions for phenomena from the core to the edge at reactor relevant parameters for each region, developing a valuable projective physics understanding. Nevertheless, it is instructive to consider what further physics gaps lie in the path to a steady state solution, and what steps (on DIII-D or elsewhere) may be valuable to develop a fuller confidence and resolve techniques and predictive models for future reactors. Two key themes emerge: (i) to access more reactor-relevant physics behaviors, and (ii) to understand the interaction between different regions and parts of the solution (e.g. high opacity plasma edge, coupled electron–ion turbulence, or super-Alfvénic ion distributions). In many cases these interactions are highly non-linear, and so important to explore in order to resolve models and be able to project integrated reactor solutions at relevant parameters.
The most critical aspect is to reconcile the core and the edge. Core and edge are strongly and non-linearly coupled, with, for instance, leakage of neutrals and impurities from closed divertor solutions impacting pedestal behavior, while requirements for pedestal performance place strong challenges on the divertor. Understanding what combined state they reach, and how they non-linearly interact, requires both regions to be in reactor relevant physics regimes. However, pedestal behavior is governed by collisionality, ν*, while a dissipative divertor solution requires radiation, primarily governed by absolute divertor density and parallel heat flux. From the basic scaling for collisionality, ν* ~ n3e /P2, (assuming a fixed mapping between divertor and pedestal density for simplicity) divertor and core cannot simultaneously operate in reactor relevant physics regimes (ne and ν* respectively) unless they are also at reactor-relevant absolute pressure. Techniques such as super-H and divertor closure can modify the mapping from divertor to pedestal top to alleviate the challenge, but further progress is needed to close the gap in ne and ν* to study a reactor-like integrated dynamic. Further, this divertor-pedestal interaction is itself altered by increasing pedestal opacity as reactor-like densities are approached, where pedestal profiles become more strongly dependent on transport and pinch effects, making exploration of higher density pedestals particularly important.
Shaping is a key lever to raise pedestal pressure; for example with higher triangularity (a rise in triangularity to 0.9 is possible with removal of the upper inner cryopump in DIII-D, Fig. 46), pedestal stability and height is improved, also increasing plasma volume and current carrying capacity, and thus overall parameter range. Combined with appropriate heating and current drive choices, a significant rise in performance in steady state conditions is projected (Fig. 47) in FASTRAN integrated modeling projections (see section "Simulation Tools"), with a tripling of pedestal height and stored energy over present steady state regimes on DIII-D. ITER-like ν*ped values would be obtained at double the present accessible density. This could help decouple ν* and density to explore high performance cores with high power more dissipative divertor configurations, and begin to understand the changes in pedestal dynamic with increasing opacity. The decoupling of ν* from Greenwald density fraction would also help to resolve the physics and critical parameters for density limit—a key enabling parameter for reactor performance and divertor dissipation. These developments would bring DIII-D close to ITER in ν*–density space (Fig. 48), though a speculative further step to raise toroidal field to 2.5T would require careful analysis, and possibly further buttressing and cooling of the structure.
Higher density steady state regimes would also close the gap on other key metrics of fusion regime relevance. Exploring the parameters in the 2.2T projection of Fig. 47 further, we see increased bootstrap fraction will enable exploration of high performance regimes that are closer to self-sustainment. This is due to the lower (and more reactor-like) fast ion fraction, which will in turn help test energetic particle physics and ideal MHD limits in more reactor relevant ways. High density will also lead to increased electron–ion collisionality to explore more equilibrated transport dynamics, and thus capture turbulent transport interactions in reactor-like electron–ion coupled regimes. This would be a significant step in testing physics over a wider range of more reactor relevant parameters to understand projection, helping close and understand key physics gaps toward future D-T fusion reactors, that is possible within present facility limits.
A further gap remains in the above argument, associated with pedestal opacity. While the above developments can enable higher density access with low collisionality pedestals, they will do so at relatively low opacity. Penetration depths for neutral ionization, ΔCX, scale predominantly with density (ΔCX = 1.91E17 T0.425ped /nped [Loarte, private communication]). At present maximum field in DIII-D, 2.17T, ΔCX is comparable to pedestal width for reactor-relevant ν*ped < 0.2, and significant influence of neutrals is observed on pedestal structure. Penetration depths can be reduced by raising density of course, but at the expense of raising ν*ped , and thus potentially altering pedestal transport mechanisms. But ΔCX reaches half the width at 3T and a third at 4T. Closing this gap would enable a facility to explore a low collisionality, transport-governed pedestal while at the same time achieving high density detached conditions. This effectively goes further down the path of understanding how non-linear interactions govern an integrated solution, rather than constraining some aspects of the model separately, and relying on the model to project integrated solutions. At 4T ITER-like absolute pedestal pressures are projected to fully explore the pedestal divertor dynamic, with thermal QDTeq ~ 1, reducing projection to reactors in a range of parameters. An advanced closed divertor would be combined with this with structure optimized to promote detachment at all radii, to develop and study detachment in the resulting high heat flux scenarios. Parallel heat flux is projected to rise a factor of 3 from 0.8 GW/m2 in steady states accessible now, to 2.9 GW/m2 at 2.5 T and an ITER-like 5.2 GW/m2 at 4T. Such a step would require a major investment in a new facility or major upgrade to DIII-D (new vessel and TF set), but would be a powerful tool to explore reactor scenario optimization in D–D before construction of a D-T device.
Conclusions
The advanced tokamak represents an exciting concept to attain the realization of fusion energy. It benefits from natural synergies between the desired plasma configuration, and the stability and transport properties that sustain them. DIII-D research in recent years has taken substantive steps in validating and developing a model based understanding of this concept. The fundamentals of current drive physics have been validated. Work has identified the critical physics governing stability limits, which point to high ideal MHD βN potential, and has pioneered advanced wall mode control schemes to extend these limits further. Similarly the processes governing energetic particle transport, which can adversely redistribute current and lead to losses, have been revealed, with advanced simulations now capturing key aspects of behavior. Effects such as further broadening of the current profile and electron heating have been demonstrated to close windows on energetic particle driven instabilities. Further, bifurcations in transport have been observed as high β plasmas have been developed, validating underlying concepts in turbulence theory and helping develop improved predictive simulation models. Current profile and local magnetic shear are found to play key roles in this behavior, which require electromagnetic and multiscale effects to be taken into account.
These favorable behaviors have formed the basis for various optimizations of the plasma internal structure, ranging from peaked to broad current profiles. Strong progress has been made in establishing the dynamics of how these work, and in demonstrating them to be viable approaches. In some cases, such as high li, βN levels have transiently reached levels close to those of the most advanced reactor concepts. Others have been used to explore the integration of key reactor elements such as radiative divertor, ELM control and low rotation operation. In all cases, significant progress has been gained in understanding the dynamics and evolution of the discharge, and its control. This is already being applied in assisting other facilities about the world, such as EAST, JT-60SA and KSTAR in development of long pulse discharges, as well as to provide guidance for ITER’s Q = 5 steady state mission.
These elements have been used to develop state of the art physics models spanning the plasma behavior, which have in turn been built into integrated modeling workflows. These workflows have not only enabled far more powerful tests of the underlying physics models, but have also provided a basis for projecting plasma operating regimes, in order to guide research, particularly upgrades to the facility. They are also now being used to scope out and explore potential performance of future reactor concepts, though this aspect lies beyond the scope of this paper.
Nevertheless, much further work remains to reach and understand how to sustain performance at reactor relevant parameters, and to validate physics in these more demanding regimes. To achieve this DIII-D has commenced a series of upgrades, with improvements to neutral beams, ECH and new current drive technologies being implemented in the 2018–19 facility opening, and further development planned over the next five year operating period. These upgrades will considerably expand current drive, electron heating and torque flexibility to access the most advanced scenarios and probe the underlying physics. They will also test three new promising, more efficient and reactor relevant current drive technologies. They will be augmented with improvements to 3D systems for transient control and innovative new approaches for safely quenching the plasma. And a parallel program will develop improved divertor concepts with increased closure. All these elements have been developed based on the latest physics understanding, utilizing state of the art physics simulations to predict requirements and performance.
The central element of this DIII-D steady state research mission is thus core–edge integration—extending beyond development simply of a high performance core or a divertor solution, but pursuing an understanding of the integration and interaction of these two, which form a natural tension in reactor design. Research in this next 5 year period will explore this interaction between the regions, providing the beginnings of the development of an integrated physics basis to design future fusion reactors. Simulations have shown how these developments can be built upon with further increases in heating and current drive capability, shaping, and possible rises in toroidal field. This has the potential to close the gap on reactor parameters in order to enable the development of integrated solutions for fusion energy and proceed with a generation of steady state fusion reactors.
Change history
19 October 2018
The article “DIII-D Research to Prepare for Steady State Advanced Tokamak Power Plants”, written by R. J. Buttery, B. Covele, J. Ferron, A. Garofalo, C. T. Holcomb, T. Leonard, J. M. Park, T. Petrie, C. Petty, G. Staebler, E. J. Strait, M. Van Zeeland, was originally published electronically on the publisher’s Internet portal (<ExternalRef><RefSource>https://doi.org/10.1007/s10894-018-0185-y</RefSource><RefTarget Address="10.1007/s10894-018-0185-y" TargetType="DOI"/></ExternalRef>) on 3 September 2018 without open access.
References
J.L. Luxon et al., Nucl. Fusion 42, 614 (2002)
J. Wesson, D.J. Campbell, Tokamaks, 3rd edn. (Oxford University Press, Oxford, 2004)
ITER Physics Basis, Nucl. Fusion 39, 2137 (1999)
M. Kikuchi et al., Plasma Phys. Control. Fusion 35, B39 (1993)
R.J. Goldston et al., Plasma Phys. Control. Fusion 36, B213 (1994)
T.S. Taylor et al., Plasma Phys. Control. Fusion 36, B229 (1994)
J.D. Galambos et al., Nucl. Fusion 35, 551 (1995)
T.C. Luce, Fusion Sci. Technol. 48, 1212 (2005)
F. Najmabadi et al., Fusion Eng. Des. 80, 3 (2006)
T.C. Luce, Phys. Plasmas 18, 030501 (2011)
A.A. Galeev, R.Z. Sagdeev, Sov. Phys. JETP 26, 233 (1968)
N.J. Fisch, Rev. Mod. Phys. 59, 175 (1987)
V. Mukhovatov et al., Chapter 9: ITER contributions for Demo plasma development. Nucl. Fusion 47, S404 (2007)
T.S. Lee et al., Fusion Eng. Des. 98–99, 1072 (2015)
G. Federici et al., Fusion Eng. Des. 89, 882 (2014)
H. Zohm, Fusion Sci. Technol. 58, 613 (2010)
H. Zohm et al., in Proceedings of 43rd EPS Conference on Plasma Physics (2016)
K. Tobita et al., Nucl. Fusion 49, 075029 (2009)
K. Kim et al., Nucl. Fusion 55, 053027 (2015)
J.S. Kang et al., in Proceedings of 26th IAEA FEC 2016 Paper FIP/3-3 (2016)
C.E. Kessel et al., Fusion Sci. Technol. 67, 1 (2015). https://doi.org/10.13182/FST14-794
B. Sorbom et al., Fusion Eng. Des. 100, 378–405 (2015)
J.E. Menard, Nucl. Fusion 56, 106023 (2016)
V. Chan et al., Physics basis of a fusion development facility utilizing the tokamak approach. Fusion Sci. Technol. 57, 66 (2010)
A.M. Garofalo et al., Fusion Eng. Des. 89, 876 (2014)
A.M. Garofalo et al., Nucl. Fusion 54, 073015 (2014)
J.P. Blanchard, C.E. Kessel et al., Fusion Sci. Technol. 68, 225 (2015)
Y.T. Song, Concept design of CFETR Tokamak machine. IEEE Trans. Plasma Sci. 42, 503 (2014)
N.J. Fisch, Fusion Sci. Technol. 65, 1 (2014)
O. Sauter et al., Phys. Plasma 4, 1654 (1997)
J.R. Ferron et al., Nucl. Fusion 51, 063026 (2011)
F. Troyon, O. Gruber, Phys. Lett. 110A, 29 (1985)
J.A. Wesson, A. Sykes, Nucl. Fusion 25, 85 (1985)
A.D. Turnbull et al., Nucl. Fusion 38, 1467 (1998)
J.E. Kinsey et al., Phys. Plasmas 13, 022305 (2006)
V.S. Chan et al., Nucl. Fusion 55, 023017 (2015)
A.M. Garofalo, X. Gong, B.A. Grierson, Q. Ren, W.M. Solomon, E.J. Strait, M.A. Van Zeeland, C.T. Holcomb, O. Meneghini, S.P. Smith, G.M. Staebler, B. Wan, R. Bravenec, R.V. Budny, S. Ding, J.M. Hanson, W.W. Heidbrink, L.L. Lao, G. Li, C. Pan, C.C. Petty, J. Qian, C. Paz-Soldan, G. Xu, Nucl. Fusion 55, 123025 (2015)
B. Wan et al., in Proceedings of 41st EPS Conference on Plasma Physics (Berlin, Germany, 23–27 June 2014) vol 38F. http://ocs.ciemat.es/EPS2014PAP/pdf/O2.104.pdf (1994)
C.T. Holcomb et al., Phys. Plasmas 16, 056116 (2009)
J.R. Ferron et al., Phys. Plasmas 20, 092504 (2013)
C.T. Holcomb et al., Nucl. Fusion 54, 093009 (2014)
R.E. Waltz et al., Phys. Plasmas 2, 2408 (1995)
E.J. Strait et al., Phys. Rev. Lett. 75, 4421 (1995)
F. Turco, C.C. Petty, T.C. Luce, T.N. Carlstrom, M.A. Van Zeeland, W. Heidbrink, F. Carpanese, W. Solomon, C.T. Holcomb, J.R. Ferron, Phys. Plasmas 22, 056113 (2015)
C.C. Petty, J.E. Kinsey, C.T. Holcomb, J.C. DeBoo, E.J. Doyle, J.R. Ferron, A.M. Garofalo, A.W. Hyatt, G.L. Jackson, T.C. Luce, M. Murakami, P.A. Politzer, H. Reimerdes, Nucl. Fusion 56, 016016 (2016)
C.C. Petty et al., Phys. Rev. Lett. 102, 045005 (2009)
S.C. Jardin et al., Phys. Rev. Lett. 115, 215001 (2015)
J.R. Ferron, C.T. Holcomb, T.C. Luce, J.M. Park, E. Kolemen, R.J. La Haye, W.M. Solomon, F. Turco, Nucl. Fusion 55, 073030 (2015)
J.M. Park et al., Comput. Phys. Commun. 214, 1 (2017)
J.M. Park, J.R. Ferron, C.T. Holcomb, R.J. Buttery, W.M. Solomon, D.B. Batchelor, W. Elwasif, D.L. Green, K. Kim, O. Meneghini, M. Murakami, P.B. Snyder, Phys. Plasmas 25, 012506 (2018)
C.C. Petty, R. Nazikian, J.M. Park, F. Turco, X. Chen, L. Cui, T.E. Evans, N.M. Ferraro, J.R. Ferron, A.M. Garofalo, B.A. Grierson, C.T. Holcomb, A.W. Hyatt, E. Kolemen, R.J. LaHaye, C. Lasnier, N. Logan, T.C. Luce, G.R. McKee, D. Orlov, T.H. Osborne, D.C. Pace, C. Paz-Soldan, T.W. Petrie, P.B. Snyder, W.M. Solomon, N.Z. Taylor, K.E. Thome, M.A. Van Zeeland, Y. Zhu, Nucl. Fusion 57, 116057 (2017)
R.J. Buttery et al. Development of a steady state fusion core: the advanced tokamak path white paper published to the National Academies of Sciences review. A Strategic Plan for U.S. Burning Plasma. online (National Academies of Sciences Engineering Medicine, 2018). http://sites.nationalacademies.org/cs/groups/bpasite/documents/webpage/bpa_185243.pdf
M.R. Wade et al., Nucl. Fusion 45, 407 (2005)
R. Nazikian et al., Nucl. Fusion 58, 106010 (2018)
W. Howl et al., Phys. Fluids B 4, 1731 (1992)
Y.R. Lin-Liu et al., Phys. Plasmas 6, 3934 (1999)
L.L. Lao et al., Phys. Fluids B 4, 232 (1992)
R.L. Miller et al., Phys. Plasmas 4, 1062 (1997)
M. Murakami et al., Nucl. Fusion 49, 065031 (2009)
V. Igochine et al., Active Control of Magneto-Hydrodynamic Instabilities in Hot Plasmas Chap. 4 (Springer, Berlin, 2015)
C.T. Holcomb et al., Phys. Plasmas 22, 055904 (2015)
C.S. Collins, W.W. Heidbrink et al., Phys. Rev. Lett. 116, 095001 (2016)
G.J. Kramer et al., Nucl. Fusion 57, 056024 (2017)
M.A. Van Zeeland et al., Nucl. Fusion 56, 112007 (2016)
D.C. Pace et al., Nucl. Fusion 57, 014001 (2017)
D.C. Pace et al., Phys. Plasmas 25, 056109 (2018)
A.M.V. Garofalo et al., Phys. Plasmas 13, 056110 (2006)
J.M. Hanson, J.W. Berkery, J. Bialek, M. Clement, J.R. Ferron, A.M. Garofalo, C.T. Holcomb, R.J. La Haye, M.J. Lanctot, T.C. Luce, G.A. Navratil, K.E.J. Olofsson, E.J. Strait, F. Turco, A.D. Turnbull, Nucl. Fusion 57, 056009 (2017)
X. Gong et al., in 25th IAEA International Conference on Fusion Energy (St Petersburg, Russia, 13–18 October 2014) http://www-pub.iaea.org/iaeameetings/46091/25th-Fusion-Energy-Conference-FEC-2014
Q.L. Ren et al., Phys. Plasmas 23, 062511 (2016)
J. Qian et al., Nucl. Fusion 57, 056008 (2017)
S. Ding et al., Phys. Plasmas 24, 056114 (2017)
J. McClenaghan et al., Nucl. Fusion 57, 116019 (2017)
C. Pan et al., Nucl. Fusion 57, 036018 (2017)
A.M. Garofalo et al., Plasma Phys. Control. Fusion 60, 014043 (2018)
M.A. Beer, G.W. Hammett, G. Rewoldt, E.J. Synakowski, M.C. Zarnstorff, W. Dorland, Phys. Plasmas 4, 1792 (1997)
T.W. Petrie et al., J. Nucl. Mater. 196–198, 848 (1992)
T.W. Petrie et al., Nucl. Fusion 37, 331 (1997)
M.R. Wade et al., Nucl. Fusion 38, 1839 (1998)
J.A. Goetz et al., J. Nucl. Mater. 266–269, 359 (1999)
A. Kallenbach et al., J. Nucl. Mater. 337–339, 732 (2005)
T.W. Petrie et al., J. Nucl. Mater. 363–365, 416 (2007)
T.H. Osborne et al., Plasma Phys. Control. Fusion 42, A175 (2000)
J.R. Ferron et al., Phys. Plasmas 12, 056126 (2005)
T.W. Petrie et al., Nucl. Fusion 57, 086004 (2017)
T.W. Petrie et al., Nucl. Mater. Energy 12, 1141 (2017). https://doi.org/10.1016/j.nme.2016.10.029
P.B. Snyder et al., Phys. Plasmas 9, 2037 (2002)
D.D. Ryutov, Phys. Plasmas 14, 064502 (2007)
V.A. Soukhanovskii et al., Phys. Plasmas 19, 082504 (2012)
D.N. Hill et al., Nucl. Fusion 53, 104001 (2013)
T.W. Petrie et al., J. Nucl. Mater. 463, 1225 (2015)
M. Murakami et al., Phys. Plasmas 13, 056106 (2006)
J.M. Park et al., Phys. Plasmas 16, 092508 (2009). https://doi.org/10.1063/1.3213614
Validation of off-axis neutral beam current drive physics in the DIII-D tokamak, in Proceedings of 24th International Conference on Fusion Energy (San Diego, CA, 2012) (Vienna: IAEA) EX/P2-13 (2012)
C.T. Hsu, K.C. Shaing, R.P. Gormley, D.J. Sigmar, Phys. Fluids B 4, 4023 (1992)
M. Taguchi, Nucl. Fusion 36, 657 (1996)
C.C. Petty et al., Phys. Rev. Lett. 83, 3661 (1999)
M. Yoshida et al., Nucl. Fusion 57, 056027 (2017)
M. Yoshida et al., Nucl. Fusion 55, 073014 (2015)
F. Turco et al., Phys. Plasmas 19, 122506 (2012)
G. Staebler et al., Phys. Plasmas 25, 056113 (2018)
G. Staebler et al., Theory of transport in high bootstrap fraction H-modes with internal transport barriers. Accepted for publication, Nuclear Fusion (2018)
S. Ding, G.S. Xu, Q. Wang, W.M. Solomon, Y. Zhao, X. Gong, A.M. Garofalo, C.T. Holcomb, G. McKee, Z. Yan, H.Q. Wang, J. Qian, B.N. Wan, Nucl. Fusion 57, 022016 (2017)
B. Hu, R. Betti, J. Manickam, Phys. Plasmas 12, 057301 (2005)
Y. Liu, M.S. Chu, I.T. Chapman, T.C. Hender, Phys. Plasmas 15, 112503 (2008)
J.W. Berkery, S.A. Sabbagh, H. Reimerdes, R. Betti, B. Hu, R.E. Bell, S.P. Gerhardt, J. Manickam, M. Podestà, Phys. Plasmas 17, 082504 (2010)
H. Reimerdes, J.W. Berkery, M.J. Lanctot, A.M. Garofalo, J.M. Hanson, Y. In, M. Okabayashi, S.A. Sabbagh, E.J. Strait, Phys. Rev. Lett. 106, 215002 (2011)
J.D. King, E.J. Strait, S.A. Lazerson, N.M. Ferraro, N.C. Logan, S.R. Haskey, J.-K. Park, J.M. Hanson, M.J. Lanctot, L. Yueqiang, R. Nazikian, M. Okabayashi, C. Paz-Soldan, A.D. Turnbull, Phys. Plasmas 22, 072501 (2015)
S. Munaretto, E.J. Strait, S.R. Haskey, N.C. Logan, C. Paz-Soldan, D.B. Weisberg, Modal analysis of the full poloidal structure of the plasma response to n = 2 magnetic perturbations. Submitted to Phys. Plasmas (2018)
O. Katsuro-Hopkins, J. Bialek, D.A. Maurer, G.A. Navratil, Nucl. Fusion 47, 1157 (2007)
S.A. Sabbagh et al., Nucl. Fusion 53, 104007 (2013)
M. Clement, J. Hanson, J. Bialek, G. Navratil, Nucl. Fusion 58, 046017 (2018)
C.C. Petty, M.E. Austin, D.P. Brennan, K.H. Burrell, J.C. DeBoo, E.J. Doyle, J.R. Ferron, A.M. Garofalo, J.C. Hillesheim, C.T. Holcomb, C. Holland, A.W. Hyatt, Y. In, G.L. Jackson, J. Lohr, T.C. Luce, M.A. Makowski, M. Murakami, M. Okabayashi, P.A. Politzer, R. Prater, H. Reimerdes, T.L. Rhodes, L. Schmitz, S.P. Smith, W.M. Solomon, G.M. Staebler, R. Takahashi, F. Turco, A.D. Turnbull, M.A. Van Zeeland, G. Wang, A.E. White, L. Zeng, AIP Conf. Proc. 1406, 497 (2011)
C.Z. Cheng, M.S. Chance, Phys. Fluids 29, 3695 (1985)
Y. Kusama et al., Nucl. Fusion 38, 1215 (1998)
H.L. Berk, D.N. Borba, B.N. Breizman, S.D. Pinches, S.E. Sharapov, Phys. Rev. Lett. 87, 1085002 (2001)
R. Betti, J.P. Freidberg, Phys. Fluids B 3, 1865 (1991)
A.D. Turnbull et al., Phys. Fluids B 5, 2548 (1993)
N.N. Gorelenkov, Phys. Plasmas 16, 056107 (2009)
M.A. Van Zeeland et al., Phys. Plasmas 14, 056102 (2007)
R. Nazikian et al., Phys. Plasmas 15, 056107 (2008)
W.W. Heidbrink et al., Plasma Phys. Controlled Fusion 46, 1855 (2004)
M.E. Austin, J. Lohr, Rev. Sci. Instrum. 74, 1457 (2003)
M.A. Van Zeeland et al., Phys. Rev. Lett. 97, 135001 (2006)
C.Z. Cheng, M.S. Chance, J. Comput. Phys. 71, 124 (1987)
W.W. Heidbrink et al., Phys. Rev. Lett. 99, 245002-1 (2007)
K.L. Wong, W.W. Heidbrink et al., Nucl. Fusion 45, 30 (2005)
M. Podesta, M. Gorelenkova, E.D. Fredrickson, N.N. Gorelenkov, R.B. White, Nucl. Fusion 56, 112005 (2016)
W.W. Heidbrink et al., Nucl. Fusion 53, 093006 (2013)
R.B. White, N. Gorelenkov, W.W. Heidbrink, M.A. Van Zeeland, Plasma Phys. Control. Fusion 52, 045012 (2010)
R.B. White, N. Gorelenkov, W.W. Heidbrink, M.A. Van Zeeland, Phys. Plasmas 17, 056107 (2010)
R.B. White, M.S. Chance, Phys. Fluids 27, 2455 (1984)
Y. Todo, M.A. Van Zeeland, A. Bierwage, W. Heidbrink, Nucl. Fusion 54, 104012 (2014)
Y. Todo, M.A. Van Zeeland, A. Bierwage, W. Heidbrink, M. Austin, Nucl. Fusion 55, 073020 (2015)
Y. Todo, M.A. Van Zeeland, W.W. Heidbrink, Nucl. Fusion 56, 112008 (2016)
W.W. Heidbrink et al., Phys. Plasmas 15, 055501 (2008)
M.A. Van Zeeland et al., Nucl. Fusion 52, 094023 (2012)
W.W. Heidbrink et al., Plasma Phys. Control. Fusion 56, 095030 (2014)
C.T. Holcomb et al., Phys. Plasmas 23, 062511 (2016)
G.Y. Fu et al., Phys. Plasmas 2, 1029 (1995)
M.A. Van Zeeland et al., Plasma Phys. Control. Fusion 50, 035009 (2008)
M.A. Van Zeeland et al., Nucl. Fusion 49, 065003 (2009)
K. Nagasaki et al., Nucl. Fusion 53, 113041 (2013)
K. Nagaoka et al., Nucl. Fusion 53, 072004 (2013)
S.E. Sharapov et al., Plasma Phys. Control. Fusion 60, 014026 (2018)
C.F. Maggi et al., Nucl. Fusion 55, 113031 (2015)
Dale Meade et al., in International collaboration in fusion energy sciences research: opportunities and modes during the ITER Era, FESAC Report February 28 2012. https://science.energy.gov/~/media/fes/pdf/workshop-reports/20120309/Intl_Collab_Final_SCSC-PRINT.pdf (2012)
JT-60SA research plan published on the web at: http://www.jt60sa.org/b/index.htm, see also J. Kamada et al., Nucl. Fus. 51 (2011) 073011
J. Stober et al. in Proceedings of 26th IAEA FEC, Kyoto (2016)
A. Bock et al., Phys. Plasmas 25, 056115 (2018). https://doi.org/10.1063/1.5024320
R. Prater et al., Nucl. Fusion 54, 083024 (2014)
R.I. Pinsker, et al. submitted to nuclear fusion (2018), also paper EX/P3-22, in Proceedings of 26th IAEA FEC Kyoto 2016, preprint GA-A28396 (2016)
G.M. Wallace et al., in Poster Presentation and Conference Proceeding, 45th European Physical Society Conference on Plasma Physics, 2–6, Prague, Czech Republic, P5.1049 (2018)
J. Candy et al., J. Phys Confer. Ser. 78, 012008 (2007)
J. Candy et al., Plasma Phys. Control. Fusion 49, 1209 (2007)
V.A. Izzo, P.B. Parks, Phys. Plasmas 24, 060705 (2017)
W.M. Solomon et al., Phys. Rev. Lett. 113, 135001 (2014)
P.B. Snyder et al., Nucl. Fusion 51, 103016 (2011)
Acknowledgements
This authors would like to pay tribute to the entire DIII-D team whose research led to the body of knowledge described in this paper. This material is based upon work supported by the U.S. Department of Energy, Office of Science, Office of Fusion Energy Sciences, using the DIII-D National Fusion Facility, a DOE Office of Science user facility, under Awards DE-FC02-04ER54698, DE-AC05-00OR22725 and DE-AC52-07NA27344. DIII-D data shown in this paper can be obtained in digital format by following the links at: https://fusion.gat.com/global/D3D_DMP. This report was prepared as an account of work sponsored by an agency of the United States Government. Neither the United States Government nor any agency thereof, nor any of their employees, makes any warranty, express or implied, or assumes any legal liability or responsibility for the accuracy, completeness, or usefulness of any information, apparatus, product, or process disclosed, or represents that its use would not infringe privately owned rights. Reference herein to any specific commercial product, process, or service by trade name, trademark, manufacturer, or otherwise does not necessarily constitute or imply its endorsement, recommendation, or favoring by the United States Government or any agency thereof. The views and opinions of authors expressed herein do not necessarily state or reflect those of the United States Government or any agency thereof.
Author information
Authors and Affiliations
Corresponding author
Additional information
The original version of this article was revised due to a retrospective Open Access order.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Buttery, R.J., Covele, B., Ferron, J. et al. DIII-D Research to Prepare for Steady State Advanced Tokamak Power Plants. J Fusion Energ 38, 72–111 (2019). https://doi.org/10.1007/s10894-018-0185-y
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10894-018-0185-y